METOD

Таблица 15 Таблица умножения для пятеричной системы счисления

б) Найдем произведение 43025 • 3245, используя правила умножения аналогичные правилам, принятым в десятичной с. с., и таблицу 15.

Запишем второй множитель под первым так, чтобы разряды совпадали:

43025

3245

Используя таблицу 15, умножим 43025 на 45.

43025

3245

332135

Рассуждали так: четыре на два 13 (по таблице); 3 пишем, 1 – в уме. Четыре на нуль дает 0, да плюс один, – пишем 1. Четыре на три 22 (по таблице); 2 пишем, 2 – в уме. Четыре на четыре 31 (по таблице), да плюс два, – пишем 3, 3 – в уме. Тройку сносим в пятый разряд.

Рассуждая аналогично, умножим 43025 на 25, полученное произведение запишем под первым результатом, смещая на разряд влево:

43025

3245

332135

141045

Умножим 43025 на 35, полученное произведение запишем под вторым результатом, смещая на разряд влево:

43025

3245

332135

141045

234115

Сложим полученные произведения, используя правило сложения в q-ной системе счисления для пятеричной с. с.:

43025

3245

332135

141045

234115

31204035

Итак, 43025 • 3245 = 31204035. Ответ: 31204035.

Задача. Записать наибольшее и наименьшее n-разрядные числа, представимые в системе счисления с основанием q и перевести эти числа в десятичную систему: n = 5, q = 4.

Решение

Наибольшее пятиразрядное число, состоящее из 3 как максимальной цифры четверичной системы счисления

333334 = 3 • 44 + 3 • 43 + 3 • 42 + 3 • 41 + 3 • 40 = 97510.

Наименьшее пятиразрядное число 100004 = 1 • 44 + 0 • 43 + 0 • 42 + 0 • 41 + 0 • 40

= 25610.

Ответ: 97510 и 25610.

Задача. Какое максимальное десятичное положительное и минимальное отрицательное числа можно представить в двух байтах информации?

Решение

Два байта – это 16 бит (т. е. 2 по 8 бит), то есть это 16-разрядное число в двоичной системе счисления. Положительное число начинается (слева) нулем, так как мы ищем максимальное число, то остальные цифры будут единицы. Итак, двоичное представление максимального положительного числа в двух

байтах информации: 0111 1111 1111 11112. Это число проще перевести в 16ную систему по таблице 12, а затем из 16-ой с. с. в десятичную:

0111 1111 1111 11112 = 7FFF16 = 7 • 163 + 15 • 162 + 15 • 161 + 15 • 160 = = 7 • 4096 + 15 • 256 + 15 • 16 + 15 = 28672 + 3840 + 240 + 15 = 3276710.

Отрицательное число начинается (слева) единицей, так как мы ищем минимальное число, то остальные цифры будут нули. Итак, двоичное представление минимального отрицательного числа в двух байтах информации: 1000 0000 0000 00002. Это число проще перевести в 16-ную систему по таблице 13, а затем из 16-ой с. с. в десятичную:

1000 0000 0000 00002 = 800016 = 8 • 163 + 0 • 162 + 0 • 161 + 0 • 160 = = 8 • 4096 + 0 + 0 + 0 = – 2867210.

Ответ: 3276710 и – 2867210.

Задача. Получить двоичную, шестнадцатеричную форму внутреннего представления чисел в двухбайтовой ячейке: 160810 и –160810.

Решение

Воспользуемся правилами получения внутреннего представления в ЭВМ целого положительного и целого отрицательного числа N, хранящегося в k- разрядном машинном слове. В нашем случае машинным словом является двухбайтное число, то есть 16-разрядное.

Переведем N = 160810 в двоичную систему счисления, получим 110010010002. Внутренне представление этого положительного числа в двухбайтовой ячейке памяти будет следующим: 0000 0110 0100 1000.

Для нахождения шестнадцатеричной формы представления числа воспользуемся таблицей 13 и получим 0648.

Для нахождения двоичной формы представления отрицательного числа – 160810 найдем обратный код положительного числа 160810, для этого:

заменим 1 на 0 в его двоичном представлении (0000 0110 0100 1000): 1111 1001 1011 0111.

Прибавим к обратному коду 1:

1 1 1

1111 1001 1011 01112

12

1111 1001 1011 10002

1111 1001 1011 1000 – это внутреннее двоичное представление отрицательного числа –160810. Его шестнадцатеричная форма: F9B8.

Ответ: 0000 0110 0100 1000 и 0648; 1111 1001 1011 1000 и F9B8.

Задачи для самостоятельного решения

I тип

Задача 50*. Число, записанное в развернутой форме, представить в сокращенной форме:

а) 1•24+0•23+0•22+1•21+1•20; б) F•163+D•162+8•161+0•160;

в) 7•85+7•84+5•83+0•82+2•81+0•80; г) 4•108+9•107+7•106+0•105+2•104+1•103+0•102+3•101+4•100; д) 2•72+6•71+6•70; е) 5•94+4•93+3•92+0•91+7•90.

Задача 51*. Число, записанное в сокращенной форме, представить в развернутом виде:

а) 21013; б) BF2D16 ; в) 5446; г) 9787510; д) A3B12;

е) 10100112.

Задача 52**. Перевести число, записанное в сокращенной форме, в десятичную систему счисления:

а) 11000102; б) CD516; в) 33124;

г) 47748; д) 32215; е) 1094710.

Задача 53***. Найти ошибку в сокращенной или развернутой записи числа:

а) 1040065; б) 76557; в) 10112012;

г) 20522123; д) F789G0316;

е) 46 + 5 • 45 + 3 • 44 + 2 • 43 + 2 • 42; ж) 5 • 64 + 2 • 33 + 2 • 62 + 4 • 6 + 5; з) 2 • 33 + 32 + 3 + 3; и) 55 + 3 • 54 + 4 • 53 + 2 • 52 + 5 + 6;

к) B • 166 + F • 164 + 9 • 163 + E • 162 + H • 16 + C.

Задача 54***. Перевести дробное число в десятичную систему счисления:

а) 0,1012; б) 0,00112; в) 0,4678; г) 0,0645; д) 0,324; е) 0,1239.

II тип

Задача 55*. Перевести дробное число из десятичной системы в q-ичную:

а) q = 4; число 0,98610; б) q=2; число 0,5610; в) q=3; число 0,12810; г) q=5; число 0,1410; д) q=6; число 0,64810; е) q=8; число 0,79110.

Задача 56**. Перевести целое число из десятичной системы в q-ичную:

десятичную:

а) 99916 → x8; б) 5667 → x4; в) 758 → x2; г) 1869 → x5;

д) 100112 → x6;

Задача 60***. Осуществить перевод числа из системы счисления с основанием 2n в другую систему с основанием 2k, используя соответствующие таблицы:

а) D1216 → x2; б) 7518 → x2; в) 12234 → x2; г) HFD32 → x2;

д) 110000112 → x4; е) 110101002 → x8;

ж) 10111100102 → x16;

з) 1111011001112 → x432.

Задача 61***. Осуществить перевод числа из системы счисления с основанием 2n в другую систему с основанием 2k через двоичную:

а) CB416 → x8; б) 4468 → x16; в) 2214 → x8; г) 62338 → x4; д) AF916 → x4; е) 21334 → x16.

IV тип

Задача 62*. Описать процесс получения результата действия и найти ошибку:

V тип

Задача 67*. Записать наибольшее и наименьшее n-разрядные числа, представимые в системе счисления с основанием q и перевести эти числа в десятичную систему:

a)n = 4; q = 2;

b)n = 3; q = 16;

c)n = 4; q = 4;

d)n = 5; q = 6;

e)n = 12; q = 7;

f)n = 4; q = 8.

Задача 68**. Какое максимальное десятичное положительное и минимальное отрицательное числа можно представить в байте информации?

Задача 69**. Получить двоичную, шестнадцатеричную форму внутреннего представления чисел в двухбайтовой ячейке:

a)145110 и –145110;

b)186710 и –186710;

c)233710 и –233710;

d)199710 и –199710;

e)198610 и –198610;

f)230010 и –230010.

Задача 70***. По шестнадцатеричной форме внутреннего представления целого числа в двухбайтовой ячейке восстановить само число:

a)F89A;

b)FA7B;

c)F8D0;

d)F9AA;

e)F8D4;

f)F7BB.

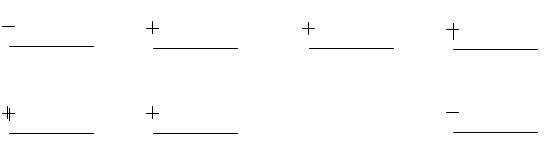
Задача 71***. Выяснить, в какой системе счисления произведено сложение, и заменить звездочки цифрами:

Задача 72***. Составить соответствующие таблицы умножения и выполнить умножение:

а) 1011012 • 1012; б) 568 • 128; в) 1204 • 314;

г) 12013 • 1103; д) А516 • 9С16; е) 5617 • 337.

Домашнее задание

Вариант 1

1.Перевести число, записанное в сокращенной форме, в десятичную систему счисления: 11001101012

2.Перевести целое число 746 из десятичной в троичную систему счисления.

4.Выполнить действие: 5278 + 6018; 3256 – 2416.

5.Получить двоичную, шестнадцатеричную форму внутреннего представления чисел в двухбайтовой ячейке 235010 и –235010.