
4 курс / Общая токсикология (доп.) / Токсикометрия эффективных доз
.pdf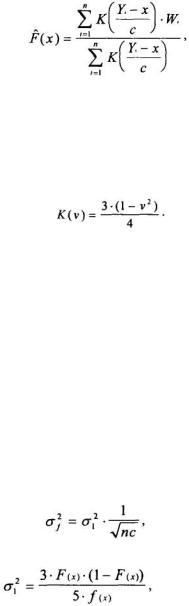
родные группы тест-объектов. Возьмем, например, обычную последовательность эффектов (1/6, 3/6, 5/6) для традиционных методов пробитанализа. В данном случае вычисленное число инверсий равно 7, а критическое значение при n1=9 и n2=9 равно 21 (см. табл. 9 приложения) при Р=0.05. Следовательно, значимость зависимости «доза-эффект» в данном случае доказана. При этом каждый результат рассматривался как независимый, повторяющийся в эксперименте, чем и обусловлено различие в выводах о значимости «доза-эффект» в случае применения методов статистического анализа для сгруппированных данных, показанных в разделе 1.3 в примерах использования дисперсионного анализа для качественных признаков.
3.3. Непараметрическое вычисление категорий эффективных доз
Потребности токсикометрии диктуют необходимость независимого определения категорий эффективных доз, минуя этап первоначального построения функции эффективности. В экспериментальной практике часто встречаются ситуации, когда функция эффективности определяется не на всем ее протяжении от ED1 до ED99, а лишь на некоторых участках. В таких случаях установить вид распределения функции эффективности невозможно. Поэтому существует необходимость разработки таких методов, которые позволяли бы производить непараметрическое вычисление отдельных категорий эффективных доз (в первую очередь ED50) по результатам независимых единичных испытаний.
Трудность решения этой проблемы состоит в поиске статистического метода преобразования результатов независимых единичных испытаний в вероятности появления эффекта в поддиапазонах испытанных доз. Анализ литературных данных позволил нам выбрать статистически адекватное решение поставленной задачи, которое состояло в использовании метода М.С.Тихова (1993,а,б), примененного автором для технических приложений.
Статистический смысл метода М.С.Тихова состоит в нахождении вероятности эффекта в центре заданного поддиапазона испытанных доз. Если в заданном диапазоне находится n значений доз (Yi) с соответствующими индикаторами эффекта (Wi), то оценка F(x) вероятности того, что гипотетическая минимальная абсолютная доза X меньше заданной в центре поддиапазона может быть найдена по следующей формуле:
(3.4)
где с — константа, значение которой будет определено ниже; х — значение категории эффективной дозы, находящейся в середине
поддиапазона испытанных доз.
Здесь функция K(v) имеет смысл весовых коэффициентов, предназначенных для уменьшения влияния на конечный результат малоинформативных крайних значений поддиапазона. Она определена в интервале -1 < ν < 1 и равна:
(3.5)
Втаком случае функция K(v/c) будет определена в интервале -с<v<с,
афункция К((ν—х)/с) — в интервале х-с < v < х+с.
Вкачестве «ядра» К(ν) могут быть использованы и другие функции, например, функция нормального распределения или функция К(ν)=COS(πν) В интервале —1≤ ν ≤ 1.
Константа с и определяемые ею поддиапазоны должны быть достаточно большими, чтобы в них попадало такое число наблюдений, которое обеспечивало бы значимость искомых оценок. Для выбора значения константы с нами были применены специальные методы численной оптимизации заданной функции, реализованные программными средствами. Отклонение функции эффективности от нормального распределения не сказывается на вычислении конечного результата, так как константа с определяет только размер интервала и выбирается в зависимости от ширины диапазона испытанных доз.
При увеличении объема выборки оценка F(x) приближается к нормальному распределению с дисперсией, равной:
(3.6)
где
(3.7)
а f(x) — плотность распределения для F(x), равная ее производной, т.е. f(x) = F'(x); n — число испытанных в заданном диапазоне доз.
В формуле (3.6) вместо 12 можно использовать ее оценку, под-
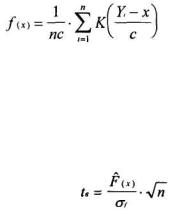
ставив вместо F(x) значение ˆ(x) , найденное по формуле (3.3), а вместо
F
f(x) можно взять ее оценку в точке х равную:
(3.8)
Для определения надежности оценки вероятности эффекта в центральной точке поддиапазона испытанных доз можно применить t- критерий Стьюдента, позволяющий установить значимость отличий вычисленного показателя от нуля. Обоснованность применения данного критерия вытекает из того факта, что вычисляемая оценка стремится к нормальному распределению при увеличении числа наблюдений. Значение t -критерия Стьюдента может быть вычислено по формуле:
(3.9)
Значимость оценки F(x) может быть определена оригинальным методом «кросс-проверки» (Хардле В., 1993), сущность которого заключается в нахождении суммы квадратов отклонений от истинного значения оценки F(x) при реализации процедуры последовательного исключения отдельных наблюдений из выборки значений, вошедших в заданный поддиапазон доз, определяемый величиной константы с. Найденный показатель представляет собой дисперсию оценки F(x), на основе которой по t-критерию Стьюдента устанавливается значимость самой оцен-
ки F(x).
Таким образом, проведено статистическое обоснование метода вычисления оценки вероятности появления эффекта в заданном поддиапазоне доз при условии испытания дозы, численно равной значению середины поддиапазона. Достоинством данного метода является то, что он относится к категории непараметрических методов, и возможность его применения не зависит от вида распределения функции эффективности. Кроме того, при увеличении числа наблюдений распределение конечных оценок приближается к нормальному закону. Соответствие приведенных положений законам теории вероятностей теоретически доказано в работах М.С.Тихова (1993,а,б) и получило одобрение и поддержку на двух Всероссийских симпозиумах по применению стохастических методов (Криштопенко СВ., Тихов М.С., 1995, 1996).
Приведенные формулы позволяют оценивать вероятность появления эффекта от испытанных доз, применительно к эффективной дозе, находящейся в середине установленного диапазона, и вычислять статисти-
ческую достоверность найденного показателя. Для вычисления доверительных интервалов самой эффективной дозы необходимо применить специальные статистические методы.
Совершенно очевидно, что испытанные дозы U измеряются с определенной ошибкой ε. Истинная величина вводимой дозы оценивается как y=U + ε. Причем, величина ошибки ε должна быть одинаковой (не больше заданной) для всех испытанных доз. Таким образом, для вычисления истинного значения среднеэффективной дозы (или другой категории эффективных доз) имеются результаты измерений испытанных в заданном диапазоне доз у1, у2,...уn. Ошибка измерения доз является нормально распределенной случайной величиной со средним значением 0 и
дисперсией 02 , на основании которой можно находить истинные зна-
чения испытанных доз. Величину σ0 можно определить как среднеквадратическое отклонение, которое определяет границы толерантного интервала выборки допустимых значений испытанной дозы при Р=0.05:

которые находятся по истинным значениям испытанных доз, определенных на основании ошибки их измерения со средним значением 0 и
дисперсией 02 с использованием таблицы случайных чисел для нормального распределения.
Значение Тп(х) может быть определено из той же формулы (3.4), что
и значение ˆ(x) .
F
Для оценки устойчивости среднеэффективной дозы к наличию ошибок в исходных данных были проведены расчеты их абсолютных значений и стандартных ошибок при разных величинах предельной относительной погрешности. Результаты вычислений приведены в табл. 3.3
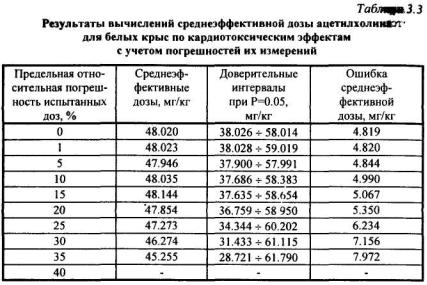
Из анализа данных, приведенных в таблице, видно, что ошибка среднеэффективной дозы с увеличением предельной относительной погрешности испытанных доз возрастает, и при 40% погрешности среднеэффективная доза по полученным исходным данным уже не определяется. Доверительные интервалы среднеэффективной дозы соответственно расширяются. При этом уменьшаются границы интервала значимых эффективных доз, определяемых по исходным данным. Так, для демонстрируемого примера в случае отсутствия ошибок измерения исходных данных функция эффективности может быть достоверно определена в
диапазоне ED36,8 – ED87,5. Но уже при погрешности равной 25% достоверно можно рассчитать только значение ED50. При погрешности 35%
исчезает устойчивость среднеэффективной дозы. Для уменьшения границ доверительных интервалов и уменьшения ошибки среднеэффективной дозы необходимо увеличивать число испытаний внутри заданного диапазона доз и расширять диапазон испытываемых доз.
Таким образом, в приведенном методе реализованы следующие основополагающие принципы:
•вычисление среднеэффективной дозы (и других категорий эффективных доз) и ее доверительных интервалов проводится непараметрически, независимо от вида распределения функции эффективности;
•не предъявляется каких-либо предварительных условий к порядку формирования исходных данных; они могут быть представлены как в сгруппированном виде, так и в виде независимых единичных испыта-
ний;
•эффективные дозы и доверительные интервалы находятся с учетом погрешности испытанных доз;
•проведение вычислений может быть выполнено без особых затруднений при помощи программных средств на ЭВМ.
3.4. Оценка нормальности распределения функции эффективности
Построение функции эффективности при помощи параметрических методов, в том числе и традиционных (Литчфилда-Вилкоксона и Финни) предполагает необходимость доказательства вида распределения функции эффективности (нормальное, логарифмически нормальное и т.д.)- Специфичность решения данной задачи заключается в том, что нормальная функция эффективности представлена только в интегральном виде и тем самым имеет отличительные особенности от стандартной функции нормального распределения для других показателей. Статистическое решение данной задачи может быть основано на следующих теоретических предпосылках.
При условии нормального распределения функция эффективности характеризуется линейной зависимостью:
xi = a + zi·σ, (3.22)
где а — среднеквадратическое отклонение (SED50); xi — категории эффективных доз (ED5, ED16, ED50 и т.д.); zi — нормированные отклонения (квантили нормального распределения) заданных категорий эффективных доз хi, соответствующие вероятностям эффектов; а — ED50.
Показатель а вычисляется обычным методом (формула 2.16) по категориям эффективных доз ED84, ED16, ED50 из линейной функции эффективности.
С учетом свойства линейности нормальной функции эффективности, можно принять критерии линейности, вычисленные по методу наименьших квадратов, в качестве первичного условного критерия нормальности, так как нормальная функция эффективности в любом случае должна быть линейной. Данное положение очевидно, но применимо не для всех случаев. Решающее значение имеет угол наклона функции эффективности к оси абсцисс. При слишком большом или слишком малом угле наклона распределение функции эффективности может существенно отличаться от нормального, что косвенно отражает значения такого показателя как положительный и отрицательный эксцесс. Данный факт вытекает из следующих теоретических предпосылок.
Приведем выражение (3.22) к виду:

(3.23)
и с учетом правила «трех сигм» (Герасимович А.И., 1983) найдем, что для нормального распределения любое значение нормированного отклонения, соответствующего заданной категории эффективной дозы, должно находиться внутри диапазона:
(3.24)
Для приведенных критических значений вероятность выхода нормированных отклонений за пределы указанного диапазона в случае нормального распределения функции эффективности равна 0.00125 (Герасимович А.И., 1983). Если принять в качестве критического уровня вероятности нулевой гипотезы Р=0.10, то выражение (3.24) примет следующий вид:
(3.25)
В конкретном виде хi отражает численное значение испытанной в эксперименте или вычисленной категории эффективной дозы (ED5,
ED45, ED84 и т.д.), σ — показатель эффективности (SED50), zi — выраженные через квантили нормального распределения наблюдавшиеся в
эксперименте частоты или вычисленные вероятности эффектов при воздействии заданной категории эффективной дозы. Для нахождения г, можно использовать либо соответствующие таблицы (Большев Л.Н., Смирнов Н.В., 1983), либо эмпирическую формулу:
Значение λ соответствует значению ˆ(x)
F
Со = 2.515517 С, = 0.802853 С2 = 0.010328
, a
d, = 1.432788 d2 = 0.189269 d3 = 0.001308
Абсолютная погрешность вычислений по формуле (3.26) не превы-
шает 4.5·10–4.
Практическое применение формулы (3.25) становится ясным из следующего примера. Пусть ED50 = 4 мг/кг, а σ = 1 мг/кг. Коэффициент ва-
риации в этом случае равен 25%. Отношение хi/σ равно 4, a zi = 0. Вычисленное значение попало в заданный диапазон, что может служить критерием нормальности функции эффективности, при условии, если и все другие категории эффективных доз не выйдут за пределы данного диапазона. Если ED50 = 2 мг/кг, а σ = 1 мг/кг, то коэффициент вариации равен 50%. Отношение хi/σ равно 2, a zi = 0. Вычисленное значение вышло за левую границу диапазона, следовательно, гипотеза о нормальности распределения функции эффективности не может быть принята. Ес-
ли ED50 = 6 мг/кг, а σ = 1 мг/кг, то коэффициент вариации равен 16.6%. Отношение хi/σ равно 6, a zi = 0. Вычисленное значение вышло за пра-
вую границу диапазона и гипотеза о нормальности распределения функции эффективности также не может быть принята. Подобные вычисления можно выполнить и в отношении любой другой категории эффективной дозы.
После применения предложенного критерия оценки нормальности распределения функции эффективности для примера, приведенного в табл. 3.1, доказано, что найденная функция эффективности не имеет значимого отличия от нормального распределения при Р=0.10.
Для случаев, когда нормальность распределения (линейность) функции эффективности не прослеживается, многие авторы предлагают проводить логарифмическое преобразование испытанных доз и повторно строить функцию эффективности. Однако, не стоит забывать, что подобные преобразования нарушают соотношения между такими показателями нормального распределения как среднее и дисперсия, а, соответственно, и вычисляемыми на их основе категориями эффективных доз. Оценки доверительных интервалов после обратного преобразования так же оказываются смещенными и создают иллюзию точности метода. Кроме того, последующие сравнения двух среднеэффективных доз, полученных путем применения подобных преобразований, при помощи параметрических критериев Стьюдента или Фишера нельзя рассматривать как корректные. Особенно опасно применение преобразований для доз, содержащих погрешности измерений. С учетом приведенных соображений становятся совершенно очевидными преимущества разработанного нами непараметрического метода.
3.5. Оценка устойчивости среднеэффективной дозы
Среднеэффективная доза является случайной величиной. Вероятность появления заданного эффекта при воздействии исследуемого токсичного вещества в дозе близкой к ED50 равна 0.5, т.е. в данном случае вероятность появления эффекта равна вероятности его отсутствия.
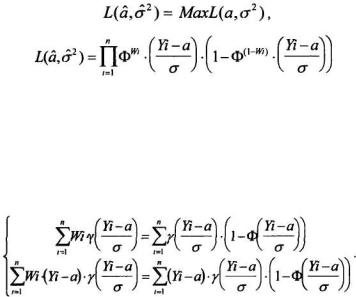
По мере удаления исследуемых доз от ED50 в левую или правую сторону вероятность эффекта соответственно стремится к 0 или 1. Из данного положения следует, что средний участок функции эффективности является наиболее неустойчивым. Сущность оценки устойчивости среднеэффективной дозы и состоит в исследовании влияния изменения эффектов от доз среднего участка функции эффективности на количественные характеристики среднеэффективной дозы.
В качестве среднего участка функции эффективности выберем интервал, определяемый односигмовым доверительным интервалом сред-
неэффективной дозы (ED50 ± SХЕD50/2). Так как при испытании доз, находящихся в указанном интервале, вероятность появления эффекта у
тест-объекта равна вероятности его отсутствия (Р=0.50), то можно обоснованно применить процедуру последовательной инвертности эффектов от испытанных в данном диапазоне доз с вычислением оценок функции эффективности (ED50 и SЕD50). Например, если при испытании указанной дозы у тест-объекта проявился отрицательный эффект, то данный эффект инвертируется на положительный и вычисляется новое значение ED50, которое по критерию Стьюдента сравнивается с исходным значением среднеэффективной дозы. Среднеэффективная доза считается устойчивой, если при инвертировании эффектов она достоверно не отличается от исходной величины.
Таким образом, критерий устойчивости среднеэффективной дозы является показателем надежности и качества результатов токсикологического эксперимента по нахождению количественных оценок токсичности исследуемых веществ, особенно при использовании малых выборок. По нашему мнению, критерий устойчивости не следует рассматривать как обязательный при вычислениях среднеэффективной дозы. Он позволяет экспериментатору в зависимости от конкретной ситуации принимать решение с большей долей надежности, если речь идет о разработке каких-либо регламентационных оценок или критериев качества.
3.6. Параметрическое построение функции эффективности и вычисление категорий эффективных доз
Задача параметрического построения функции эффективности сводится к нахождению оценок параметров а (ED50) и σ (SED50) по исходным данным, представленным в виде независимых единичных испытаний (Yi, Wi). В том случае, если предварительно доказано, что функция эффективности существенно не отличается от нормального распределения, то можно с помощью современных методов математической стати-
стики найти ее окончательные параметры.
Анализ методов математической статистики позволил нам найти следующий методический подход к решению этой задачи.
В случае, когда предполагается нормальное распределение случайной величины X, плотность ее распределения равна:
 (3.28-3.29)
(3.28-3.29)
где параметры -∞<а<∞, σ>0 — неизвестны. Оценки этих параметров можно определить по методу максимального правдоподобия Фишера (Клепиков Н.П. и соавт., 1964):
(3.30-3.31)
Известно, что уравнение правдоподобия имеет единственное решение, состоятельную, асимптотически нормальную и асимптотически эффективную оценку искомых параметров.
Если обозначить через Y(x) функцию, равную отношению Ψ(x) к Ф(х)·(1–Ф(x)), то после математических преобразований решение уравнения (3.31) сведется к решению системы двух уравнений с двумя неизвестными (а и σ):
(3.32)
Решение приведенной системы уравнений может быть произведено численными методами (Вознесенский В.А., 1981; Герасимович А.И.,1983; Гринчишин Я.Т. и соавт., 1988) или методом стохастической аппроксимации (Вазан М.Т., 1972). Численные методы предполагают задание начальных оценок искомых величин для последующего поиска
конечных параметров, удовлетворяющих решению системы уравне- |
38.8 мг/кг - 0/1; |
ний с заданной точностью. В качестве начальных оценок ED50 и SED50 |
40.0 мг/кг - 0/1; |
можно обоснованно принять значения, найденные при помощи непара- |
42.0 мг/кг - 0/1; |
метрического метода. |
44.0 мг/кг - 0/1; |
После нахождения конечных значений ED50 и SED50 дальнейшее вы- |
46.0 мг/кг - 1/1; |
числение категорий эффективных доз по нормальной функции эффек- |
48.0 мг/кг - 1/1; |
тивности с использованием общепринятых методов не представляет за- |
50.0 мг/кг - 1/1; |
труднений. |
52.0 мг/кг - 1/1. |
Для примера, приведенного в табл. 3.1, оценки нормально рас- |
Среднеэффективная доза составила 45.0±2.3 (39.5÷50.5) мг/кг. Пре- |
|
пределенной функции эффективности, найденные параметрическим ме- |
дельная относительная погрешность испытанных в этом случае может |
|
тодом, оказались следующими: ED50=48.3 мг/кг, SED50=10.9 мг/кг, |
достигать 9%, а значение среднеэффективной дозы составит 45.1±7.9 |
|
SXED50=2.7 мг/кг. Вычисленные по функции эффективности категории |
(26.4÷63.8) мг/кг. При больших значения погрешности доз среднеэф- |
|
эффективных доз равны: ED5=22.8 мг/кг, ED16=33.3 мг/кг, ED84=64.6 |
фективная доза не определяется. Но в указанных примерах среднеэф- |
|
мг/кг, ED95=75.3 мг/кг и т.д. |
фективная доза не имеет устойчивости, так как в испытаниях прослежи- |
|
Отметим, что идея использования метода максимального прав- |
вается резкий переход эффектов с 0 (доза 44.0 мг/кг) на 1 (доза (46.0 |
|
доподобия для построения функции эффективности ранее уже вы- |
мг/кг), и инвертность эффекта приводит к значимому изменению сред- |
|
сказывалась отдельными авторами (Володин В.П., 1986; Cornfield J., |
неэффективной дозы, что и регистрируется как ее неустойчивость. При |
|
Mantel N., 1950). |
дополнении испытаний (см. табл. 3.1) среднеэффективная доза оказа- |
|
Таким образом, для построения функции эффективности по ре- |
лась устойчивой при инвертности эффектов, что можно расценивать как |
|
зультатам независимых единичных испытаний можно использовать два |
ее надежность. |
|
подхода: непараметрический, когда распределение функции эффектив- |
Сравним возможности непараметрического метода с методом Прозо- |
|
ности отличается от нормального и параметрический — при нормаль- |
ровского. Возьмем исходные данные, приведенные в примере 1 раздела |
|
ном распределении функции эффективности. Но не следует забывать, |
2.8.1: |
|
что адекватное применение метода максимального правдоподобия |
200 мг/кг - 0/2; |
|
предполагает использование исходных данных, измеренных без оши- |
250 мг/кг - 1/2; |
|
бок. Ясно, что этот факт не позволяет рассматривать данный метод как |
316 мг/кг- 1/2; |
|
универсальный. |
398 мг/кг - 2/2. |
|
3.7. Возможности непараметрического метода вычисления категорий |
Значение среднеэффективной дозы, вычисленное по табл.5 при- |
|
ложения, составило 282 (160÷418) мг/кг для модели логарифмически |
||
эффективных доз |
||
нормального распределения функции эффективности и стандартных |
||
Для практического применения непараметрического метода вы- |
||
ошибках среднего значения 52 и 58 при Р=0.05. Непараметрический ме- |
||
числения категорий эффективных доз мы постарались показать его воз- |
тод при использовании тех же исходных данных дал следующий ре- |
|
можности в сравнении с известными методами, приведенными во вто- |
зультат среднеэффективной дозы при условии ее нормального распре- |
|
рой главе. |
деления — 299±58 (161÷437) мг/кг. Как видно, результаты вычислений |
|
Первым является вопрос о минимальном количестве испытаний для |
оказались весьма близкими. Однако, среднеэффективная доза в этом |
|
определения достоверной среднеэффективной дозы и других |
случае не является устойчивой по соответствующему критерию. |
|
категорий эффективных доз. Уже при 8 испытаниях, если предельная |
В примере 2 метода Прозоровского для случая: |
|
относительная погрешность доз не превышает 1%, можно определить |
1.6 мг/кг - 1/2; |
|
значение и доверительные интервалы среднеэффективной дозы. Так, |
2.0 мг/кг - 1/2; |
|
например, по результатам эксперимента: |
2.5 мг/кг - 1/2; |
3.2 мг/кг-2/2
не прослеживается значимая зависимость «доза-эффект», так как вычисленное число инверсий по критерию Вилкоксона-Манна-Уитни составило 3, а критическое – 1 для Р=0.05. Поэтому вычисление значения среднеэффективной дозы по приведенным исходным данным нельзя рассматривать как корректное. При увеличении числа испытаний:
1.6 мг/кг - 1/3;
2.0мг/кг - 1/3;
2.5мг/кг-2/3;
3.2мг/кг-3/3
вычисленное число инверсий по критерию Вилкоксона-Манна-Уитни составило 4, а критическое — 6 для Р=0.05. Вычисление среднеэффективной дозы в этом случае допустимо. По методу Прозоровского оно составило 2.08 (1.8÷2.4) мг/кг, а по непараметрическому методу — 2.3±0.4 (1.4÷3.2) мг/кг. При этом среднеэффективная доза также является неустойчивой. Для повышения ее устойчивости и надежности необходимо дополнить испытания в середине диапазона.
Особый интерес представляет анализ ситуации применения указанных методов для случая тестирования веществ с низкой биологической активностью в плане того, что конечный результат в большей степени зависит от полноты и качества исходных данных, нежели от метода расчета. Так, по исходным данным
20.0 мг/кг - 0/2;
40.0 мг/кг - 1/2;
80.0 мг/кг - 1/2;
160.0 мг/кг - 2/2
среднеэффективная доза, вычисленная по методу Прозоровского при помощи табл. 7 приложения, оказалась равной 56 (21÷106) мг/кг. Непараметрический метод не позволяет вычислить значение среднеэффективной дозы, так как для данного случая не прослеживается нормального распределения среднеэффективной дозы. По этой же причине результаты вычислений по методу Прозоровского нельзя рассматривать как надежные. После проведения дополнительных испытаний
20.0мг/кг-0/3;
40.0мг/кг- 1/3;
80.0мг/кг-2/3; 160.0 мг/кг -3/3,
вычисленная по методу Прозоровского при помощи табл. 7 приложения среднеэффективная доза составила 56 (34÷85) мг/кг. Непараметрический метод дал значение нормально распределенной средне-
эффективной дозы равное 87.4±26.9 (28.1÷146.7) мг/кг. Причиной такого значения среднеэффективной дозы и широкого доверительного интервала является неопределенность исходных данных, что и обусловило большое значение среднеэффективной дозы и широкий доверительный (вероятностный) интервал, так как диапазон между дозами 80.0 мг/кг и 160,0 мг/кг, который по сути является определяющим, оказался не испытанным. Увеличение числа испытания на тех же дозах:
20.0 мг/кг - 0/4;
40.0 мг/кг - 1/2;
80.0 мг/кг - 3/4;
160.0 мг/кг - 4/4
позволило вычислить по методу Прозоровского при помощи табл. 7 приложения среднеэффективную дозу равную 56 (39÷72) мг/кг. При использовании непараметрического метода результат остался практически тем же 86.2±21.5 (40.4÷132.2) мг/кг. Если теоретически можно было бы дополнить испытания в диапазоне доз 80.0-160.0 мг/кг и получить следующие результаты
20.0 мг/кг - 0/4;
40.0 мг/кг - 1/4;
80 0 мг/кг - 3/4;
100.0 мг/кг - 3/4;
120.0мг/кг - 4/4;
160.0мг/кг - 4/4,
то среднеэффективная доза, вычисленная при помощи непараметрического методы составила бы 60.8±11.9 (36.2÷85.4) мг/кг. В этом случае произошла стабилизация функции эффективности, а найденная среднеэффективная доза наиболее правдоподобно соответствует полученным результатам испытаний. Из приведенных примеров можно сделать тот простой вывод, что при нормальном распределении функции эффективности разные методы дают сходные результаты. Но если распределение функции эффективной отклоняется от нормального, что совершенно очевидно для случая тестирования веществ с низкой биологической активностью, то предпочтение необходимо отдавать адекватным методам, в которых либо заложены механизмы оценки вида распределения функции эффективности, либо они относятся к категории непараметрических и их точность определяется качеством исходных данных.
Непараметрический метод позволяет успешно решать задачи вычисления среднеэффективной дозы по двум точкам. Так, например, по результатам испытаний:
8.0 мг/кг - 3/10;
12.0 мг/кг - 8/10
значение среднеэффективной дозы оказалось равным 9.8±0.8 (8.1÷11.5) мг/кг.
Непараметрический метод может хорошо работать и в асимптотической области, где находятся категории эффективных доз (ED1, ED5, ED10, ED90, ED95, ED99 и т.д.). Кроме того, программными средствами нами реализован алгоритм поиска достоверных диапазонов определения категорий эффективных доз. Обратимся еще раз к результатам испытаний, приведенным в табл. 3.1. Для вычисления крайних категорий эффективных доз находящихся в асимптотической области, необходимо проведение дополнительных испытаний в этих областях. Так, по полученным исходным данным определяются крайние значения категорий эффективных доз ED36,8=42.7±3.0 (36.4÷49.0) мг/кг и ED87,5=61.8±3.4 (54.8÷68.9) мг/кг. При дополнительном испытании доз с результатами:
16.0 мг/кг - 0/1;
18.0 мг/кг - 0/1;
20.0 мг/кг - 0/1;
22.0 мг/кг - 0/1;
24.0 мг/кг - 0/1;
26.0 мг/кг - 0/1;
28.0 мг/кг - 0/1;
30.0 мг/кг - 0/1;
72.0 мг/кг - 1/1;
74.0 мг/кг - 1/1;
76.0 мг/кг - 1/1;
78.0мг/кг - 1/1;
80.0мг/кг - 1/1
стало возможным определить все категории эффективных доз: ED1=30.0±2.7 (24.5÷35.4) мг/кг;
ED5 = 32.1±3.7 (25.3÷39.0) мг/кг;
ED16= 38.4±3.1 (32.2÷44.7) мг/кг;
ED84= 61.5±5.4 (50.5÷72.5) мг/кг;
ED95 = 66.0±4.6 (56 7÷75.3) мг/кг;
ED99= 67.7±3.7 (60.2÷75.2) мг/кг.
Если по тем же исходным данным методом максимального правдоподобия Фишера построить функцию эффективности, имеющую нормальное распределение, и вычислить из нее те же категории эффективных доз, то получим следующие результаты:
ED1 = 14.9 мг/кг
ED84 = 64.6 мг/кг
ED5 = 22.8 мг/кг
ED95 = 75.3 мг/кг
ED16 = 32.3 мг/кг
ED99 = 86.4 мг/кг.
Их анализ показывает, что дозы ED16 и ED84 не очень сильно отличаются от таковых, вычисленных непараметрическим методом, в то время как остальные категории эффективных доз явно смещены на края нормального распределения. Это явление можно объяснить тем, что линейная функция нормального распределения хорошо аппроксимирует категории эффективных доз в средней ее части, а асимптотическая область функции эффективности имеет большую крутизну по сравнению с функцией нормального распределения. Поэтому краевые эффективные дозы более предпочтительно и статистически адекватно определять при помощи непараметрического метода.
Непараметрический метод работает не только с исходными данными, представленными в виде независимых единичных испытаний, но и может определять значения категорий эффективных доз для сгруппированных данных, используемых в традиционных методах вычисления среднеэффективной дозы (Литчфилда-Вилкоксона и Финни). Так, например, среднеэффективная доза, вычисленная при помощи непараметрического метода по обычным исходным данным:
8.0 мг/кг - 1/6;
10.0мг/кг-3/6;
12.0мг/кг-5/6
оказалась равной 10.00±0.95 (7.99÷12.01) мг/кг. Метод ЛитчфилдаВилкоксона, примененный с учетом логарифмически нормального распределения, дал следующие результаты — 9.86 (8.58÷11.35) мг/кг, а ме-
тод Финни — 9.88 (7,39÷2.92) мг/кг Анализируя полученные среднеэффективные дозы, можно отметить,
что они не только достоверно не различаются, но и имеют практически равные доверительные интервалы, хотя и были определены принципиально разными методами. Подобное сходство объясняется тем, что для сравнения мы умышленно использовали исходные данные с оптимальным соотношением эффектов и функция эффективности близка к нормальному распределению. В других ситуация подобного сходства может и не наблюдаться. При этом не следует забывать, что эффективность метода определяется не близостью получаемых оценок в сравнении с другими методами, а его статистической адекватностью.
Таким образом, на сравнительных примерах показаны возможности
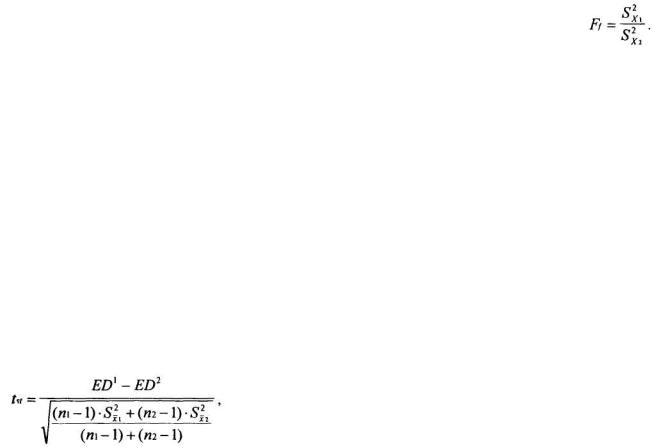
и преимущества непараметрического метода для самых разных исходных данных, что еще раз доказывает его универсальность, которая наряду со статистической адекватностью составляет основу для широкого практического использования в токсикометрии.
Глава 4 - Методы сравнения эффективных доз
Вычисление категорий эффективных доз по экспериментальным данным преследует конечную цель их сравнения для формулировки выводов о фармакологических и токсикологических особенностях тестируемых веществ. При этом, в основном, решаются две задачи. Первая включает оценку достоверности различий двух эффективных доз, а вторая предполагает вычисление относительных показателей (коэффициентов), представляющих собой отношение эффективных доз. К примеру, такие показатели как защитный индекс (коэффициент защиты), фармакологический индекс, показатель безопасности и другие широко применяются при фармакологической, токсикологической и гигиенической оценке лекарственных препаратов и опасных химических веществ. Отдельные методы сравнения эффективных доз на основе применения пробит-анализа подробно приведены в книге М.Л.Беленького (1963). Но поскольку мы рассматриваем эту проблему с позиций современных требований математической статистики и теории вероятностей, то представляется необходимым детальнее рассмотреть статистические предпосылки для ее решения.
4.1. Методы сравнения двух эффективных доз
В данном разделе будут рассмотрены два вопроса: оценка достоверности различий и способ вычисления ошибки отношений двух эффективных доз.
Оценку достоверности различий двух эффективных доз, найденных в соответствии с порядком, приведенным в разделе 3.3, целесообразно проводить при помощи t-критерия Стьюдента:
(4.1)
где ED1, ED2 — категории эффективных доз; Sx — ошибки эффективных доз.
Если вычисленное значение t-критерия Стьюдента окажется больше критического значения для заданного уровня вероятности Р (0.05, 0.01 и т д.), приведенного в табл. 1 приложения при числе степеней свободы f=(ni-1)+(n2-1)=ni+n2-2, то различие между двумя дозами можно считать статистически достоверным, и наоборот
Однако, прежде чем проводить оценку достоверности различий двух эффективных доз по t-критерию Стьюдента, необходимо проверить статистическую гипотезу о равенстве дисперсий при помощи критерия Фишера (Лакин Г Ф., 1990).
Критерий Фишера определяется как отношение большей дисперсии эффективных доз к меньшей:
(4.2)
Если вычисленное значение критерия Фишера превышает критическое значение для заданного уровня вероятности Р (0.05, 0 01 и т.д.) для степеней свободы f1=n1-1 и f2=n2-1, приведенное в табл. 2 приложения, то дисперсии эффективных доз следует признать различными (т.е. принадлежащими к разным генеральным совокупностям). В таком случае проводить оценку достоверности различий самих эффективных доз не имеет смысла, так как уже доказано, что они не принадлежат к одной генеральной совокупности (т е достоверно различаются).
Отметим, что применение критерия Фишера нашло отражение в известной книге М.Л.Беленького (1963) и других работах, как процедура оценки параллельности прямых «доза-эффект» для двух сравниваемых веществ, по той причине, что угол наклона прямых к оси абсцисс является производной величиной показателя среднего квадратичного отклонения (или дисперсии). В этом случае параллельность прямых «дозаэффект» отражает равенство дисперсий двух эффективных доз.
Для вычисления относительных показателей производится деление двух эффективных доз. Так как эффективные дозы сами являются случайными величинами, то частное от деления выборочных средних также имеет собственную ошибку, количественное выражение которой можно найти при помощи соответствующих статистических процедур. Ошибка отношения двух эффективных доз в математической статистике рассматривается как ошибка частного от деления выборочных средних с их ошибками:
