4 курс / Общая токсикология (доп.) / Токсикометрия эффективных доз

В дальнейшем оказалось, что даже пробитное смещение эффектов по оси ординат не всегда приводит к желаемому результату — линеаризации кривой «доза-эффект» (функции эффективности). Поэтому некоторые авторы предложили пользоваться различными преобразованиями значений испытанных доз на оси абсцисс. Так, Гэддэм предложил вместо абсолютных значений доз использовать их десятичные логарифмы (Беленький М.Л., 1963), Г.Н.Першин (1950) обосновал применение ряда Фульда при исследовании возрастающих доз.

Таким образом, в обобщенном виде пробит-анализ предназначен для определения линейной зависимости между дозами (или их логарифмами) и эффектами, выраженными в пробитах:

где а — свободный член уравнения, определяющий расстояние до точки пересечения прямой с осью абсцисс; b — коэффициент, численно равный тангенсу угла наклона, образованного прямой и осью абсцисс.

Тривиально считается, что доказательство линейности модели (2.15) является одновременно и отражением ее соответствия нормальному или логарифмически нормальному распределению. Условность этого допущения вытекает из следующих фактов.

Обратная величина коэффициента b из уравнения (2.15) является оценкой среднего квадратического отклонения SED50. Эту же оценку, согласно закону нормального распределения, можно получить из следующего соотношения:

(2.16)

В токсикометрии коэффициенту b придается особое значение, как показателю токсичности ядов. В случае логарифмически нормального распределения, величина равная 105 получила тривиальное название «функция токсичности» (5). По нашему мнению, эту величину правильнее называть показателем токсичности, а в общем случае — показателем эффективности, о чем уже было сказано выше. Считается, что чем меньше значение показателя токсичности, тем вещество более токсично, и наоборот. Однако, не следует забывать и тот факт, что при нормальном или логарифмически нормальном распределении значение среднего квадратического отклонения (показателя эффективности) может колебаться в строго определенном диапазоне, заданным плотностью нормального распределения. При слишком малых значениях среднего квадратического отклонения, в сравнении со средним значением выборочной совокупности, наблюдается острогорбый эксцесс, а при больших значениях - плоскогорбый. Нормальное распределение по показателю эксцесса имеет строгие ограничения. Поэтому, показатель эффективности, а следовательно и угол наклона функции эффективности к оси абсцисс, в случае нормального распределения не может принимать любые значения, а находится в строго установленных допустимых границах. В пробит-анализе данный факт остается без внимания, что, по нашему мнению, является одним из его скрытых недостатков.

На определенном этапе развития токсикометрии в виду отсутствия средств вычислительной техники для практического применения про- бит-анализа была разработана специальная логарифмически-пробитная сетка. На ней по оси абсцисс откладывались дозы в логарифмическом измерении, а по оси ординат — эффекты, выраженные в процентах и преобразованные в пробиты. Логарифмически-пробитная сетка позволяет визуально строить линейную зависимость «доза-эффект».

На недостатки пробит-анализа обращали внимание ряд авторов (Прозоровский В.Б., 1962; Урбах В.Ю., 1963, 1975; Куликов М.А., Ма-

лашенко Ю.Р., 1966; Bass R., Gunzel P., 1982; Balls M, 1991 и др.). На-

пример, О.Н.Елизарова (1971) откровенно указывает, что «кривые летальности, наблюдаемые в опыте, чаще не подчиняются этому (нормальному) закону распределения, поэтому кажущаяся точность пробитанализа является лишь иллюзорной, так как все выводы основываются на весьма недостоверной гипотезе о нормальности кривой эффекта». В.Ю.Урбах (1975) также считает, что слабым пунктом пробит-анализа является допущение о нормальности кривой «доза-эффект». Главными положениями пробит-анализа являются:

•подбор исходных данных для их включения в линейную модель

(2.15);

•оценка точности проведения прямой «доза-эффект», т.е. значимости этой модели;

•выбор способа расчета среднеэффективной дозы и ее ошибки, исходя из вычисленных параметров линейной модели.

Именно способ решения указанных проблем и положен в основу разных методов пробит-анализа. Рассмотрим и проанализируем их особенности с учетом совокупных сведений об основах пробит-анализа.

2.6.2. Метод Миллера и Тейнтера

В 1947 году Миллер и Тейнтер опубликовали работу, в которой было предложено оригинальное и по тем временам передовое решение проблемы расчета среднеэффективной дозы. Этот метод и положил начало классическому пробит-анализу. В отличие от предыдущих методов, он не устанавливал ограничений ни со стороны равномерности интервалов испытанных доз, ни со стороны равенства числа тест-объектов в группах.

Расчет среднеэффективной дозы по методу Миллера и Тейнтер проводится следующим образом (Miller L.S., Tainter M.L., 1944). Вначале на логарифмически-пробитную сетку наносятся экспериментальные точки, соответствующие логарифмам доз и пробитам эффектов. Для доз, вызвавших 0 и 100% эффекты, используется преобразование, по которому рассчитываются так называемые «рабочие пробиты» для нулевых частот

(2.17)

где N—число тест-объектов в группе.

Для 100% частот эффектов «рабочие пробиты» рассчитываются формуле:

(2.18)

Прямая между экспериментальными точками проводится визуально с помощью прозрачной линейки. При этом рекомендуется учитывать расположение экспериментальных точек. Так, точки имеют тем больший «вес», чем ближе они расположены к пробиту 5. Точки, расположенные на уровне пробитое 4 и 6, имеют «вес» равный 2/3, а точки, соответствующие пробитам 3 и 7, имеют «вес» равный 1/5 «веса» точки с пробитам 5. Из графика определяются значения величин ED50, ED16 и ED84, соответствующие пробитам 5, 4 и 6, и вычисляется среднее квад-

ратическое отклонение по формуле (2.16).

Стандартная ошибка среднеэффективной дозы вычисляется по формуле:

(2.19)

где N' — общее число тест-объектов в группах, для которых значения пробитое на оси ординат находятся между 3.50 и 6.50.

Доверительный интервал для среднеэффективной дозы вычисляется из t-распределения Стьюдента со степенью свободы f = N’ - 1 и заданным уровне вероятности p (см. табл.1 приложения).

(2.20)

Анализируя метод Миллера и Тейнтера можно отметить некоторые вызывающие сомнения методические подходы.

Во-первых, это субъективность проведения прямой между экспериментальными точками. Но этот недостаток метода не является главным, и со временем он был довольно просто устранен другими исследователями. Так, в работе М.А.Куликова и Ю.Р.Малашенко (1966) предложено проводить объективную оценку точности проведения прямой «дозаэффект» с использованием формулы Вебера:

(2.21)

где w — коэффициент значимости; Р — эмпирическая частота появления эффекта в группе тест-объектов при данной дозе; Q — эмпирическая частота отсутствия эффекта в группе при той же дозе (Q=1-Р); Z— значение функции плотности нормального распределения.

При расчете предполагается находить сумму квадратов отклонений эмпирических точек от исследуемой прямой по формуле:

(2.22)

где w— коэффициент значимости для каждой точки из формулы (2.21); n — число тест-объектов в группе; yt — эмпирическая доля положительных эффектов при данной дозе; Yi — ожидаемая доля положительных эффектов, найденная по теоретической прямой.

Меньшая величина V определяет наиболее точную прямую в серии визуально проведенных прямых.

Во-вторых, использование Миллером и Тейнтером так называемых «рабочих пробитов» для 0 и 100% эффектов не согласуется с представлением о фиксированной средней частоте появления эффекта в каждой экспериментальной точке, которая согласно биномиальному распределению должна оставаться постоянной и стремиться к среднему значению по мере увеличения числа наблюдений. Преобразование же частот по формулам (2.17) и (2.18) приводит к тому, что при увеличении числа наблюдений частоты эффектов стремятся к 0 и 100% соответственно.

В-третьих, формулу (2.19), предложенную Миллером и Тейнтером для вычисления стандартной ошибки среднеэффективной дозы, следует отнести к эмпирическим, так как она не отражает свойств нормального распределения.

2.6.3. Метод Литчфилда-Вилкоксона

Дальнейшее совершенствование пробит-анализ получил в работах J.T.Litchfield, F.H.Wilcoxon (1949) и других авторов. Было предложено вычислять стандартную ошибку логарифма среднеэффективной дозы по следующей формуле (Беленький М.Л., 1963):

(2.23)

где N’ — число тест-объектов, использованных при испытаниях доз соответствующих пробитам от 4 до 6; 1/b — оценка среднего квадратического отклонения SED50, которое вычисляется по формуле (2.16).

Оценку ошибки коэффициента b модели (2.15) предложено находить по следующей формуле:

(2.24)

где L — разность логарифмов большей и меньшей из испытанных доз; k — число испытанных доз.

J.T.Litchfield, F.H.Wilcoxon (1949) предложили проводить проверку точности визуально проводимой прямой по критерию хи-квадрат и использовать номограммы для выполнения вычислительных операций. С этого времени данный метод и получил название метода ЛитчфилдаВилкоксона. В дальнейшем он претерпел ряд усовершенствований уже другими авторами, что, однако, не коснулось его названия. В модифика-

ции З.Рота применение в номограмном варианте метода ЛитчфилдаВилкоксона с оценкой адекватности визуального проведения прямой по критерию хи-квадрат детально изложено в работе М.Л.Беленького

(1963).

В настоящее время с появлением вычислительных средств эта модификация метода Литчфилда-Вилкоксона имеет только историческое значение, хотя иногда и используется отдельными исследователями.

Дальнейшее развитие метода Литчфилда-Вилкоксона шло по пути применения процедуры регрессионного анализа для построения линейной модели «доза-эффект».

Итак, определим, что метод Литчфилда-Вилкоксона содержит следующие принципиальные положения:

•построение линейной модели «доза-эффект» (2.15) и оценка ее адекватности (статистической значимости) любым из методов, приведенных в следующем разделе;

•определение из этой модели логарифмов эффективных доз ED50,

ED16 и ED84;

• последующий расчет по формуле (2.25) оценки среднего квадратического отклонения S для случая нормального распределения функции эффективности:

(2.25)

Если же предполагается логарифмически нормальное распределение, то показатель эффективности находится по формуле:

(2.26)

Расчет так называемого «фактора fED50», отражающего значение стандартной ошибки среднеэффективной дозы умноженной на квантиль функции нормального распределения ( SED50· tα), проводится по формуле:

(2.27)

где N` — общее число тест-объектов в группах, в которых «ожидаемый» эффект от испытанных доз находится между пробитами 4 и 6.

Нетрудно заметить, что формула (2.27) является результатом логарифмически нормального преобразования выражения (2.23), умноженного на значение аргумента функции нормального распределения (1.96)

при Р=0.05.

Доверительный интервал среднеэффективной дозы при логарифмически нормальном распределении функции эффективности определяется путем деления и умножения ED50 на значение фактора fED50, т.е. из соотношения:

Для случая нормального распределения функции эффективности знаки деления и умножения в формуле (2.28) заменяются соответственно на знаки разности и сложения.

Формула (2.29) для расчета ошибки fED50 также является результатом преобразования выражения (2.24) с тем лишь отличием, что значение показателя A находится по номограммам (Беленький М.Л., 1963):

Все остальные усовершенствования не затрагивают основной сути метода Литчфилда-Вилкоксона.

2.6.4. Построение одномерной линейной регрессионной модели «до- за-эффект» и оценка ее адекватности

Задача построения одномерной линейной регрессионной модели «доза-эффект» (функции эффективности) сводится к вычислению значений коэффициентов уравнения (2.15). Впервые в отечественной литературе для решения этой задачи В.Б.Прозоровским и соавт. (1962) было предложено использование метода наименьших квадратов. Для последующего анализа его достоинств и недостатков, мы сочли необходимым показать его применение в алгоритмическом виде, удобном для статистической обработки и программной реализации.

Регрессией называется зависимость среднего значения (непостоянная функция) какой-либо величины от значений некоторой другой величины или от значений нескольких величин. Регрессионная модель показывает насколько в среднем изменяется у при изменении х.

Параметры линейной регрессионной модели x ˆ ˆ , опреде- y a bx

ляющей значение y x при использовании п пар значения х и у, рассчитываются по следующим рабочим формулам:

(2.30)

(2.31)

Эмпирические показатели регрессии величины случайные и сопровождаются статистическими ошибками. Стандартная ошибка коэффициента b может быть определена по формуле:

(2.32)

Величина Н носит название фактора гетерогенности. Если величины х неслучайны, а у — нормально распределены

имеет хи-квадрат распределение с (n-2) степенями свободы, а H/(n-2) может служить несмещенной оценкой σ2.

Считается, что линейная регрессионная модель является достоверной в том случае, если вычисленное значение H/ σ2 находится в границах

(2.33)

где 2 — квантиль порядка О < γ < 1, т.е. Р(χ2< 2 ) = γ и находит-

ся по таблицам распределения хи-квадрат.

Значение Н может быть вычислено по следующей рабочей формуле:

(2.34)

Значимость коэффициента b можно определить по t-критерию Стьюдента:

Если tS (вычисленное значение) больше t (табличное, оно же крити-

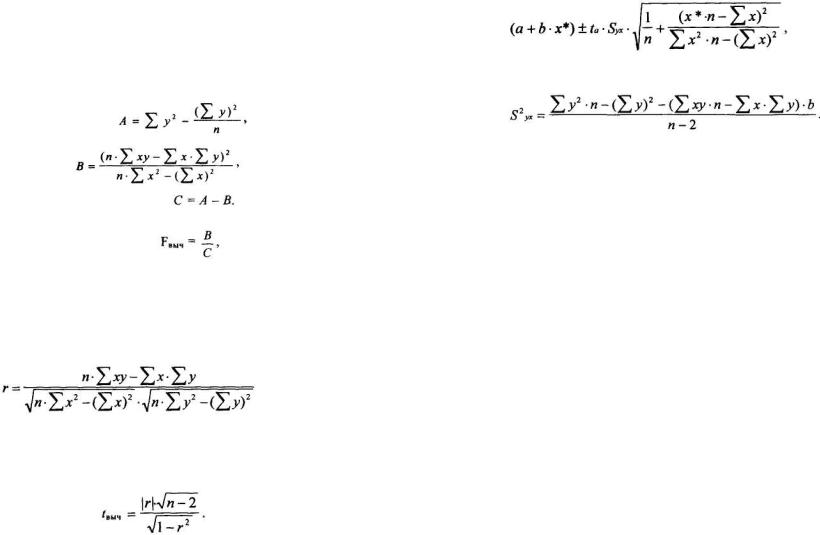
ческое) при степени свободы f=n-2 и вероятности ошибки Р=0.05 (см. табл.1 приложения), то коэффициент b признается значимым.

В случае, когда дисперсия σ2 неизвестна, оценку адекватности (достоверности) модели «доза-эффект» можно провести по однофакторному дисперсионному анализу.

Вычисляется значение показателей общей дисперсии (А), регрессионной дисперсии (В) и остаточной дисперсии (С):

(2.36)

(2.37)

(2.38)

Вычисляется эмпирическое значение критерия Фишера Fрасч.:

(2.39)

которое сравнивается с критическим (табличным) значением Fтабл при степенях свободы fв = 1 и fc = п-2 и заданном уровне вероятности ошиб-

ки Р=0.05 (см. табл.2 приложения). Если Fрасч > Fтабл, то линейная регрессионная модель признается достоверной.

В случае нормального распределения такая оценка может быть проведена по значимости коэффициента корреляции:

. (2.40)

Оценка адекватности линейной регрессионной модели проводится путем вычисления эмпирического значения t-критерия Стьюдента (tвыч) и сравнения его с критическим (табличным) значением (tтабл) при f=n–2, приведенным в табл.1 приложения.

(2.41)

Если tвыч > tтабл при степени свободы f=n–2 и уровне вероятности ошибки Р=0.10, то модель признается достоверной.

Последующее использование линейной регрессионной модели «дозаэффект» для расчета категорий эффективных доз ED50, ED16 и ED84 возможно только в том случае, если доказана ее адекватность.

Доверительные интервалы для любого значения у, найденного из линейной регрессионной модели «доза-эффект», рассчитываются по фор-

муле (2.42) (Львовский Е.Н., 1982):

(2.42)

где Syx — дисперсия, обусловленная линейной регрессией. Она рассчитывается по формуле (2.43):

(2.43)

Из формулы (2.42) следует, что самый узкий доверительный интервал имеют значения, находящиеся в середине исследуемого диапазона доз, т.е. близкие к ED50. По мере удаления от среднего значения доверительный интервал искомой величины увеличивается.

Сравнивая формулы (2.33), (2.34) и (2.43), нетрудно заметить, что величина S2yx является фактором гетерогенности Н.

В отдельных работах (Маненко А.К., Иванова О.П., 1988) приводятся иные толкования доверительных границ категорий эффективных доз, которые не согласуются с законами математической статистики.

При необходимости можно вычислить не только значение среднеэффективной дозы, но значения других категорий эффективных доз, на-

пример ED5, ED95 и т.д.

Таким образом, применение метода наименьших квадратов для построения линейной регрессионной модели «доза-эффект» явилось значительным усовершенствованием пробит-анализа, по сравнению с визуальным построением прямой «доза-эффект» по экспериментальным точкам на графике.

Однако применение метода наименьших квадратов для решения задач пробит-анализа в свою очередь привело к возникновению ряда новых проблем. Так, классическая схема линейного регрессионного анализа основана на предположении о том, что все исходные данные, содержащиеся в матрице переменной х (дозы), соответствуют истинным значениям и не содержат ошибок.

В экспериментальной практике дозы, как правило, измеряются с ошибками, иногда весьма значительными. Так, еще в работах М.А. Великанова (1962) и В.П. Бородюк (1970) показано, что ошибки независимых переменных приводят к существенному уменьшению коэффициента корреляции, коэффициента b (т.е. к возрастанию показателя эффективности) и, в конечном итоге, — к снижению достоверности самой линейной регрессионной модели «доза-эффект».

Кроме того, классическая схема пробит-анализа предполагает обрат-

ное определение средних значений эффективных доз (т.е. независимой

переменной x ) по той же модели «доза-эффект», предназначенной для определения средних значений пробитов (т.е. зависимой переменной

y ). Свойство ортогональности линейных регрессионных моделей ис-

ключает эту возможность (Федоров В.В., Успенский А.Б., 1975; Львовский Е.Н., 1982). Указанное действие возможно производить только при условии функциональной связи между переменными, когда коэффициент корреляции равен 1. Непрогнозируемые ошибки вычислений эффективных доз при игнорировании ортогональных свойств модели (2.15) будут увеличиваться по мере уменьшения коэффициента корреляции между переменными.

В таких случаях обоснованным было бы применение для построения функции эффективности сложного конфлюентного анализа (Николаева Л С, Федоров В.В., 1970). Но этот путь решения проблемы «дозаэффект» не следует рассматривать как оптимальный с учетом недостатков самого пробит-анализа.

Для устранения несоответствий, возникающих по причине ортогональности линейной регрессионной модели, можно было бы использовать в качестве независимой переменной величины пробитов и строить модель вида:

(2.44)

Однако, в этом случае частоты эффектов, а следовательно и сами пробиты, будут иметь еще большую неопределенность при малых числах тест-объектов в группах, что было показано в предыдущей главе.

Кроме того, для адекватного применения регрессионного анализа необходимо, чтобы оба признака в равной мере обладали случайной вариацией. Как отмечено в работе П.Ф.Рокицкого (1973), в биологических исследованиях возможны случаи, когда из двух изучаемых признаков только один свободно варьирует, значения же второго признака являются строго фиксированными. В таких ситуациях возможна только односторонняя регрессия. В случае зависимости «доза-эффект» свободно варьируют только значения эффектов, а значения доз являются строго фиксированными. Поэтому по рассмотренным причинам применение для расчета среднеэффективных доз моделей вида (2.44) является невозможным.

Нельзя обойти вниманием и тот факт, что статистическая оценка линейности регрессионной модели не является одновременно оценкой нормальности зависимости «доза-эффект», как это ошибочно предпола-

гают некоторые исследователи. Напомним, что функция эффективности

икоэффициент о модели (2.15) при нормальном распределении эффективных доз может находится в строго определенном диапазоне числовых значений. При этом критерии оценки линейности модели «дозаэффект» (2.15) ни каким образом не связаны с критериями оценки нормальности, так как в первом случае определяется точность линейной аппроксимации по экспериментальным точкам, а во втором — соответствие этих точек плотностям нормального распределения. Например, при малом угле наклона прямой «доза-эффект» к оси абсцисс даже в случае абсолютно линейного расположения точек на графике, нормальности функции эффективности может и не наблюдаться по критерию эксцесса или по причине большого значения коэффициента вариации. Покажем обоснованность данного положения на следующем гипотетическом примере.

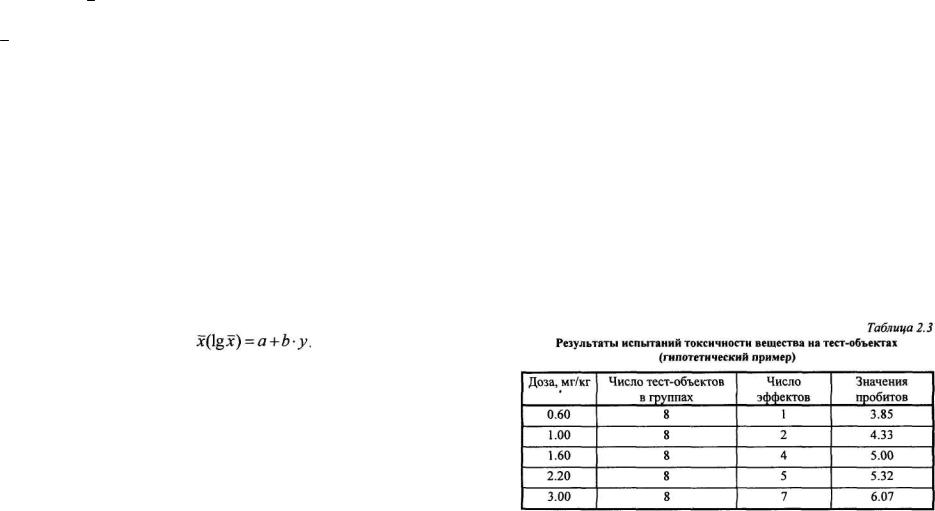
Допустим, что при испытании токсичности какого-либо вещества на тест-объектах получены исходные данные, приведенные в табл. 2.3. По методу наименьших квадратов построена линейная регрессионная модель «доза-эффект», определены значения показателей ее адекватности

ивеличины среднеэффективных доз, вычисленные по пробит-методу Литчфилда-Вилкоксона по дозам и логарифмам доз (см. табл. 2.3 и 2.4).

Анализ данных, приведенных в табл. 2.4, показывает, что несмотря на статистически подтверждаемое наличие линейной зависимости «до- за-эффект», интерпретировать результаты расчета среднеэффективной дозы как надежные нельзя, по причине больших значений коэффициентов вариаций. Они значительно превышают критическое значение коэффициента вариации, равное 33% для нормального и логарифмически нормального распределения.

Чтобы не нарушить последовательности изложения материала, рассмотрим проблему связи между линейностью пробитой модели «дозаэффект» и нормальностью распределения функции эффективности в следующей главе.

2.6.5. Метод Финни

Развитием пробит-анализа можно считать предложение Фйнни использовать для построения зависимости «доза-эффект» взвешенные значения эффектов, выраженные в пробитах, с учетом числа тестобъектов в группах. Метод Финни получил широкое распространение среди исследователей и алгоритм его применения опубликован во мно-

гих работах (Finney D.J., 1979, 1985; Debanne S.M., Haller H.S., 1985 и

др.). Включение данного метода в Государственную фармакопею СССР

в 1987 году можно считать его официальным признанием. Приведем краткое изложение метода Финни в работе S.M.Debanne, H.S.Haller (1985).

По методу наименьших квадратов (см.раздел 2.6.4.) или по методу последовательных приближений (итераций) строится линейная регрессионная модель (2.45.), определяющая зависимость между дозами (xi) или логарифмами доз (lgxi) и «весами» эффектов (zi), заданными в каждой экспериментальной точке (i):

Значение zi задано числом тест-объектов в группе (ki) и весовым ко-

Весовой коэффициент определяется ординатой плотности нормального распределения пробитов (fi), соответствующей вероятности эф-

фекта (Fi) в каждой экспериментальной точке

(2.47)

где

(2.48)

Адекватность модели (2.45) оценивается по t-критерию Стьюдента (см. 2.35) и по критерию хи-квадрат (см. 2.33). В случае признания модели адекватной, вычисляется значение среднеэффективной дозы на оси абсцисс, соответствующее средневзвешенному значению преобразованных по формуле (2.46) эффектов на оси ординат.

Доверительные интервалы рассчитываются по формуле Драйпера и Смитта:

(2.49)

где

(2.50)

(2.51)

(2.52)

(2.53)

где S — стандартная ошибка линейной регрессионной модели (2.45); t — значение t-распределения Стьюдента при степени свободы f=n-1 (n- число точек, использованных для построения модели).

Величина g отражает значимость ˆi угла наклона модели (2.45) и b

увеличивается, если абсолютное значение уменьшается. Линейная регрессионная модель «доза-эффект» (2.45) не может быть использована

для обратного нахождения эффективных доз до тех пор, пока не установлена значимость угла наклона. Считается, что модель (2.45) является адекватной в том случае, если значение g не превышает 1.

Способ вычисления среднеэффективной дозы по методу Финни изложен в виде алгоритмов в Государственной фармакопее СССР (1987).

ты, wi — весовые коэффициенты. Преобразование процентов в пробиты, и определение весовых коэффициентов проводится по табл. 3 и 4 приложения.

2. Вычисляются промежуточные показатели:

3. Вычисляются конечные показатели:

(2.54)

(2.55)

(2.56)

где X50 — среднеэффективная доза ED50; X50(н,в) — нижняя и верхняя границы ED50.

При использовании логарифмов доз, для вычисления конечных показателей производится обратное преобразование показателей X50 и

X50(н,в).

Анализ пробит-метода Финни показывает, что в нем реализован частный случай построения линейной регрессионной модели по взвешенным значениям независимой переменной. Сопоставление метода Финни с другими методами пробит-анализа позволяет сделать вывод об их принципиальных различиях. Эти различия касаются не только применения в методе Финни весовых коэффициентов, но и подходов к расчету доверительных интервалов среднеэффективной дозы. Применяемая в методе Финни для расчета доверительных интервалов формула (2.49) предполагает их вычисление на основе ошибки линейной регрессионной модели (2.45). Сравнивая формулы (2.42) и (2.49), можно отметить их идентичность. А это означает, что доверительный интервал среднеэффективной дозы по методу Финни вычисляется на основе линейной модели «доза-эффект», а не на основе среднего значения функции эффективности и показателя эффективности, как это принято в других методах пробит-анализа Функция эффективности, как таковая, в методе Финни не определяется, и даже искажается вследствие использования весовых коэффициентов, которые предназначены в статистических методах для более точного нахождения средних значений. По этим причинам метод Финни не пригоден для определения других категорий эффективных доз, кроме среднеэффективной. Другие же методы пробитанализа (Миллера и Тейнтера, Литчфилда-Вилкоксона) предполагают расчет доверительных интервалов среднеэффективной дозы на основе среднего квадратического отклонения с учетом числа испытаний в заданном интервале доз. В этих случаях линеаризованная функция эффективности определена на всем протяжении (кроме асимптотических участков) и не имеет искажений, что принципиально допускает возможность вычисления других категорий эффективных доз.

При использовании метода Финни особенно повышаются требования к качеству исходных данных. Если исходные данные (испытанные дозы) измерены с ошибками, то после выполнения процедуры «взвешивания» ошибка конечного результата становится непредсказуемой.

С биологической точки зрения подход к использованию весовых коэффициентов в методе Финни вызывает некоторые сомнения. В математической статистике весовые коэффициенты предназначены для уменьшения влияния на вычисляемое среднее значение показателя малоинформативных отдаленных от середины распределения значений. В методе же Финни в структуру весовых коэффициентов введены значения числа тест-объектов в группах, что сомнительно с биологической точки зрения, так как в этом случае имеет место не только связь «дозаэффект», но и связь числа тест-объектов в группе с эффективными доза-

Применение данного метода основано на линейной зависимости «до- за-эффект» и предположении о нормальном распределении функции эффективности, и в случае нарушения этих требований результаты вычислений могут быть ошибочными.

2.6.7. Экономичный метод определения среднеэффективной дозы и угла наклона (показателя эффективности)

На основе пробит-анализа разработаны многие методы расчета среднеэффективной дозы и угла наклона (показателя эффективности) линейной модели «доза-эффект», направленные на экономичное, хотя и менее точное, вычисление конечного результата. К этим методам можно отнести метод «одной точки» Ван-дер-Вардена, изложенный выше метод «двух точек» и другие. По нашему мнению, наибольшего внимания заслуживает метод, приведенный в работе C.S.Weil (1983), сущность которого мы излагаем.

Угол наклона b линии «доза-эффект» (см.формулу 2.15) может быть вычислен по формуле (2.64):

(2.64)

где Pr84 и Pr16 – пробиты для 84% и 16% эффектов. Показатели logED84 и logED16 вычисляются по формуле:

logEDP = D' + d·Φ, (2.65)

где р — процент эффективности для ED84 соответствующий Р=0.84; d — логарифм геометрического фактора (шага) между уровнями доз; Ф — показатель, вычисляемый по формуле (2.66);

D' — показатель, вычисляемый по формуле (2.67).

(2.66)

где п — постоянное число тест-объектов в группах;

r — число регистрируемых эффектов в заданных группах; К — число дозовых уровней, использованных для расчета.

(2.67)

Правильное применение данного метода предполагает соблюдение граничных условий. Уровни испытанных доз должны соответствовать логарифмической шкале с равномерным шагом, число тест-объектов в группах должно быть одинаковым.

Рассмотрим применение данного метода на следующем простом

примере (Weil C.S., 1983). Допустим в результате эксперимента были получены исходные данные, по которым произведен расчет искомых показателей.

В результате вычислений получены данные, по которым можно рассчитать среднеэффективную дозу (ED50) и среднее квадратическое отклонение (SED50). Для этих целей может быть использована формула (2.16), по которой вычисляется среднее квадратическое отклонение на основании свойства нормального распределения, согласно которому среднеэффективная доза определяется как среднее значение между

logED84 и logED16. В данном примере ED50= 46.7 мг/кг, logSED50= 0.511 и SED50 = 3.25.

Анализируя изложенный метод можно отметить, что в его основу положен принцип линейной интерполяции. Это придает ему сходство с методом «двух точек». Недостатки данного метода очевидны, они те же, что и в других методах пробит-анализа.

Кроме методов вычисления среднеэффективных доз на основе про- бит-анализа многими авторами были предложены и другие математические подходы для решения этой проблемы (Прозоровский В.Б. и соавт., 1978, 1980, 1983; Буслович С.Ю., Ашельрод А.А., 1989; Molinengo L., Orsetti M, 1986; Carlos S, 1987; Sevcik C, 1987; Sheftel V.O., Sova R,