
4 курс / Общая токсикология (доп.) / Токсикометрия эффективных доз
.pdf
1992; Schaper M.H. et al., 1994).
Таким образом, на примере рассмотренных методов построения функции эффективности и вычисления категорий эффективных доз определены основы пробит-анализа, его достоинства и недостатки. Основным недостатком пробит-анализа является априорное допущение о том, что частоты наблюдавшихся эффектов сразу же принимаются в качестве вероятностей (квантилей) нормально распределенной функции эффективности испытанных доз. Причем, статистическими методами это допущение не доказывается. Вид функции эффективности определяется механизмами действия тестируемого вещества, которые реализуются в чувствительности тест-объектов. Выполненные эксперименталь- но-теоретические оценки позволили определиться в том убеждении, что пробит-анализ в его разных модификациях с точки зрения математической статистики не является совершенным методом построения функции эффективности и решения проблемы расчета категорий эффективных доз. Кроме того, очевиден тот факт, что дальнейшая разработка проблемы «доза-эффект» на основе пробит-анализа не может рассматриваться как перспективная и требует иных методических подходов.
2.7. Метод расчета среднеэффективной дозы при помощи арксинусного преобразования Фишера
Линеаризация кривой «доза-эффект» возможна не только посредством пробитного преобразования частот эффектов, но и путем использования преобразований других типов. Примером такого преобразования частот эффектов может быть арксинусное преобразование Фишера (Гублер Е.В., 1978). В результате такого преобразования появляется возможность использования линейной регрессионной модели вида (2.68) для построения функции эффективности (Debanne S.M., Haller H.S., 1985).
(2.68)
где z – преобразованные по формуле (1.10) в радианы значения частот эффектов в группах.
Правильное использование данного метода предполагает наличие одинакового числа тест-объектов в группах. Определение параметров и адекватности модели (2.68) проводится по методу наименьших квадратов (см. раздел 2.6.4.). Среднеэффективная доза вычисляется по формуле:
(2.69)
Доверительные интервалы среднеэффективной дозы вычисляются по формуле (2.70) с учетом величины t-критерия Стьюдента (ta) со степенью свободы f = п–2 (п — количество испытанных доз) при заданном значении Р (см. табл. 1 приложения).
(2.70)
(2.71)
(2.72)
(2.73)
Анализ метода расчета среднеэффективной дозы при помощи арксинусного преобразования Фишера позволяет выявить его недостатки, связанные с неопределенностью частот эффектов в группах при малых числах тест-объектов, с обратным вычислением значений категорий эффективных доз по модели «доза-эффект», с неконтролируемыми погрешностями испытываемых доз и т.д. Подобные недостатки уже были проанализированы ранее. Ясно, что метод вычисления среднеэффективной дозы при помощи арксинусного преобразования Фишера, также как и пробит-метод, принимает за основу первоначальное построение нормальной функции эффективности, что нельзя считать оптимальным решением проблемы «доза-эффект».
2.8. Экспресс-методы определения среднеэффективной дозы и ее ошибки
2.8.1. Метод Прозоровского
Понимая практические трудности в реализации классических методов пробит-анализа, многие авторы направляли усилия на разработку простых, удобных в экспериментальной практике методов оценки среднеэффективной дозы и ее доверительных интервалов. Так, в 1978 году коллективом авторов (Прозоровский В.Б. и соавт.) предложен экспрессметод определения среднеэффективной дозы и ее доверительных интервалов по 8-12 наблюдениям. Нахождение дозы и ее ошибки проводится

по таблицам и не требует расчетов. Изложим с некоторыми сокращениями обоснование и сущность данного метода согласно работе В.Б.Прозоровского и соавт. (1978).
Регистрируя в нескольких группах опытов частоту возникновения определенного эффекта в ответ на какое-либо воздействие, интенсивность которого нарастает от группы к группе, можно построить кривую «доза-эффект», основным параметром которой является средняя эффективная доза — ED50.
Поскольку речь идет о малом числе наблюдений, то для определения достоверности результатов можно использовать формулу, приведенную
в руководствах П.Ф.Рокицкого (1961, 1973 ). Если ED50= X , то она достоверна при
Поскольку
(где N — общее число животных) и учитывая, что ED84 – ED16 = 2S, находим:
 . (2.74)
. (2.74)
Отсюда следует, что при малом угле наклона кривой «доза-эффект», когда величина ED84 – ED16 близка к нулю, то
(2.75)
может быть достаточно большой, даже при N =2.
Согласно формуле, приведенной П.Ф.Рокицким (1973), число опытов, необходимых для получения достоверной средней, равно:
(2.76)
Если для исходных данных использовать указание Н.А.Плохинского (1970) на то, что при нормальном распределении даже при большом разбросе наблюдений величина редко превышает 20% от средней, то, приняв, что ED50 = 1,0, имеем σ = 0.2.
Исходя из необходимости использовать малое число наблюдений, примем N=9. При этом число степеней свободы f = N-1 = 8, а t, найденное по таблице Стьюдента, равно 2.31. Из руководства П.Ф.Рокицкого
(1973) следует, что возможная ошибка опыта составит:
Поскольку
то = 0.067·2.31 = 0.115. Тогда
 .
.
Это значит, что 9 есть то количество наблюдений (опытов, животных), которое достаточно для получения достоверной средней в большинстве экспериментов.
Поскольку кривая «доза-эффект» может быть разной крутизны, в части опытов потребуется использовать меньшее, а в части — большее число наблюдений. Для того и другого случая составлены специальные таблицы.
Расчет ED50 в табл. 5 и 6 приложения произведен на основе предложенной авторами методики с использованием метода наименьших квадратов и пробит-анализа. Ошибки вычислены по методу Миллера и Тейнтера. По Бартлетту, отсутствие эффекта у 2 животных из 2 принято равным 12%, а наличие — 88%, отсутствие эффекта у 3 животных из 3
— равным 8%, а наличие — 92%. Для получения доверительных границ ошибки должны быть умножены на t, равное при уровне вероятности 0,95 и 8 опытах 2.36 (при 12 опытах — 2.2). В первом случае при 8 наблюдениях для выполнения эксперимента необходимы 4 группы по 2 наблюдения в каждой.
После предварительного ориентировочного определения эффективной дозы, исследуемые объекты подвергаются воздействию, численно равному 4 последовательным дозам из числа приведенных в первой строке табл. 6 приложения. Эти дозы соответствуют логарифмам 1.0, 1.1, 1.2,...,1.9. Данная школа взята только потому, что с величинами такого порядка чаще приходится сталкиваться в практической деятельности. Реальные дозы могут отличаться от предлагаемых в 10, 100, 1000 раз и т.д., т.е. дозы 10.0, 12.6, 15.8... и т.д. могут быть прочитаны как
1.00, 1.26, 1.58... или 100, 126, 158... При этом соответственно будет ме-
няться и порядок определяемой величины. На пересечении горизонтальной строки, соответствующей полученным результатам, и вертикальной колонки, соответствующей первой из испытанных доз, находим величину ED50 и размах ее отклонений в пределах ошибки. Для практического использования данного метода приведем примеры, взятые из
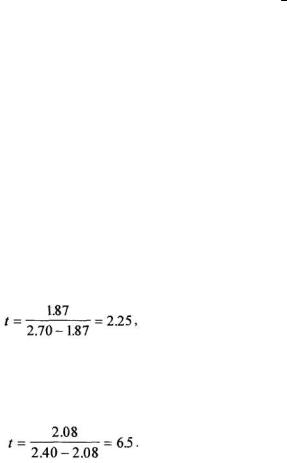
работы В.Б.Прозоровского и соавт. (1978).
Пример 1. Испытаны 4 дозы яда: 200, 250, 316 и 398 мг на кг массы тела. В 1-й группе от дозы 200 мг/кг не погибло ни одно животное — результат равен 0, во 2-й группе погибло 1 животное из 2 — результат равен 1, в 3-й — тоже 1, в 4-й группе погибло 2 животных из 2 — результат равен 2. Последовательность результатов 0, 1, 1, 2 (из 2). Находим эти цифры в 5-й строке табл. 6 приложения. На пересечении этой строки с колонкой, соответствующей первой из испытанных доз — 200
(в табл. 5 приложения — 20.0), получаем искомую величину ED50± S x
(в данном случае LD50), которая равна 282(230÷340) мг/кг. Для получения доверительных границ умножаем 340-282=58 и 282—230=52 на 2.36 (t0,05 при числе степеней свободы n–1 = 7). Полученные результаты (132 и 122) относим к среднему и получаем доверительные границы с 95% вероятностью (160÷418). Смещение среднего от центра между доверительными границами определяется использованием логарифмической шкалы.
Поскольку дозы отложены на логарифмической шкале, правильней было бы находить доверительный интервал через логарифм ошибки: lg58 + lg2.36 = 2.1363. Обратный логарифм, найденный путем потенцирования, равен 137. Вторая ошибка соответственно равна 123. Нетрудно убедиться, что уточнение незначительно и практически им можно пренебречь.
Пример 2. При определении токсичности яда в дозах 1.6, 2.0, 2.5 и 3.2 мг/кг получен эффект в 1, 1, 1, 2 случаев из 2. По табл. 5 приложения находим ED50=1.87(1.30÷2.70). Делением средней на большую из ошибок определяем:
что меньше, чем tO,05=2.36 при 8 наблюдениях. Поскольку средняя недостоверна, дополняем каждую дозу по 1 животному. Получаем результат: 0, 0, 1, 1. Общий итог из трех животных: 1, 1, 2, 3. По табл. 6 приложения уточненная средняя равна 2.08(1.8÷2.4). Делением ее на ошибку находим:
Следовательно, уточненная средняя достоверна, а конечный результат среднеэффективной дозы с учетом t0,05=2.20 при 12 наблюдениях составил 2.08 (1.5÷2.8) мг/кг.
Такова сущность экспресс-метода определения средней эффективной
дозы и ее ошибки в изложении его авторов. В процессе использования данного метода авторы установили, что составленные таблицы позволяют оценивать среднеэффективную дозу лишь по кривым, расположенным круто, с коэффициентом вариации меньше 17%. Для веществ с пологими кривыми «доза-эффект» авторы предлагают использовать новый табличный метод определения среднеэффективной дозы веществ с низкой биологической активностью, который мы и цитируем по работе (Прозоровский В.Б., Прозоровская М.П., 1980).
Как и прежде, для определения ED50 рекомендуется использовать 4 дозы, но их логарифмы должны различаться на 0.3. Характеристики логарифмов могут быть любыми целыми отрицательными или положительными числами.
Практически, для определения ED50 необходимо, исходя из какихлибо теоретических соображений, аналогий или предварительных экспериментов, ориентировочно наметить порядок ожидаемых доз: десятые доли, единицы, десятки, сотни и т.д. мг/кг, мг/л, г/м3 и т.п. Числовые значения доз берутся из первой строки табл. 7 приложения с соответствующей коррекцией (в таблице приведены десятки). Избранные дозы могут лежать в пределах одного порядка или переходить с одного порядка в другой
Если кривая расположена относительно круто, то может оказаться, что для получения достоверной средней достаточно испытаний только двух объектов на дозу. Например, при введении вещества в дозах 20, 40, 80, 160 мг/кг из каждых двух животных на дозу погибло 0/2, 1/2, 1/2, 2/2. Для нахождения средней летальной дозы по табл. 7 приложения в столбце «Последовательность реакций» находят полученный результат: 0, 1, 1, 2. На этой строке против первой из испытанных доз (в данном случае в столбце под дозой 20) отыскивают величину DL50=56 мг/кг.
Поскольку дозы расположены в логарифмической шкале и ошибки исчислены в логарифмах, то при переходе к числовым значениям ошибок они оказываются разновеликими. Ошибка, откладываемая в сторону больших доз, превышает ошибку, откладываемую в сторону меньших доз. Обе ошибки приведены в табл. 7 приложения под значениями средних. Для определения доверительных границ ED50 каждую из ошибок необходимо умножить на коэффициент t, найденный по таблице Стьюдента (см. табл.1 приложения). При 8 наблюдениях (7 степеней свободы) и вероятности ошибки Р=0.05 этот коэффициент равен 2.36, при 12 наблюдениях — 2.2 и при 16 наблюдениях — 2.13. В приведенном выше примере доверительные границы будут равны (56 - 15·2.36) ÷ (56 + 21·2.36), т.е. ED50 = 56(21÷106) мг/кг. При необходимости сузить дове-
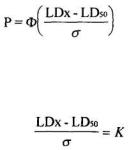
рительные границы опыты могут быть дополнены испытанием Зяго и 4- го животного на дозу. Например, при использовании 3 животных в разбираемом опыте можно ожидать результат 0, 1, 2, 3 и LD50 = 56(34÷85)
мг/кг, 4 животных — 0, 1, 3, 4 и LD50 = 56(39÷72) мг/кг. Таблица составлена таким образом, чтобы проводить оценку последовательно увеличи-
ваемых групп. Попытки испытать сразу группы по 4 наблюдения могут привести к получению таких результатов, которых нет в таблице.
Анализ табличных методов определения среднеэффективной дозы показывает, что в их основу положены эмпирические допущения, не имеющие строгого статистического обоснования. Так, для расчета ошибки среднеэффективной дозы использована эмпирическая формула (2.19) из пробит-метода Миллера и Тейнтера, а преобразования 0 и 100% частот эффектов осуществляется по условному допущению Бартлетта. Нельзя расценивать как корректное принятие частот эффектов 0 из 2 за 12%, а 2 из 2 — за 88%. В данном случае совершенно очевидна неопределенность и неустойчивость показателей частот эффектов, а следовательно, обоснованность вычисления по ним доверительных интервалов ED50, имеющих строго определенное статистическое выражение при Р=0.05, вызывает явные сомнения.
Табличный метод определения среднеэффективной дозы веществ с низкой биологической активностью, предназначенный для доз с коэффициентами вариаций 17...48%, не в полной мере согласуется с основным положением математической статистики о том, что при нормальном распределении коэффициент вариации не может превышать 33%. Это несоответствие становится понятным из следующего примера.
Допустим, что нижняя и верхняя границы доверительного интервала для дозы 13 и последовательности реакций 0, 0, 2, 2 (из 2) при Р=0.05 согласно табл.8 приложения соответственно равны:
36–11·2.36 = 10, 36+15·2.36 = 71.
Но если появится необходимость вычислить по тем же исходным данным доверительный интервал при уровне вероятности Р=0.01, то окажется, что нижняя граница попадает в область отрицательных значений:
36–11·3.50 = –2.5, 36+15·3.50 = 78.5.
Такие же исходы можно получить и для других значений доз, приведенных в табл. 8 приложения. Это стало возможным по причине несоответствия распределения среднеэффективной дозы как нормальному закону, так и распределению Стьюдента.
Из указанных соображений табличные методы определения среднеэффективной дозы не следует считать оптимальным решением проблемы расчета среднеэффективной дозы по малым выборкам. Данный метод можно использовать только для приближенной оценки диапазона колебаний среднеэффективной дозы. При этом не следует применять строго установленные статистические понятия вероятностей попадания значений среднеэффективной дозы в вычисленные доверительные интервалы. Кроме того, в основе этих методов лежат положения пробитанализа с присущими ему недостатками.
2.8.2. Метод Фрумина
Продолжением развития экспресс-методов определения среднеэффективной дозы явился метод, предложенный Г.Т.Фруминым (1991). Представим сущность метода в изложении автора.
Предполагается, что кумулятивная кривая (кривая зависимости накопленных частот особей, имеющих данный признак, от дозы) для большинства химических веществ аппроксимируется функцией нормального распределения. Правомерность этого предположения подтверждена анализом опытных данных различных авторов, в ходе которых определяли значения коэффициентов вариации. В результате проведенного анализа для 319 веществ было установлено, что асимметричные распределения имеют место лишь для 30 веществ, что составляет 9.4%. Таким образом, предположение о нормальности распределения с учетом указанного ограничения приблизительно для 10% веществ имеет право на признание.
В связи с этим наблюдаемые в эксперименте кривые эффекта, соответствующие графикам функции нормального распределения, будем описывать следующим уравнением:
, |
(2.77) |
где Р — вероятность эффекта, соответствующая дозе LDx; σ — средне квадратическое отклонение; Ф(х) — номинальная функция распределения.
Обозначим
(2.78)
Тогда после несложных преобразований получим:
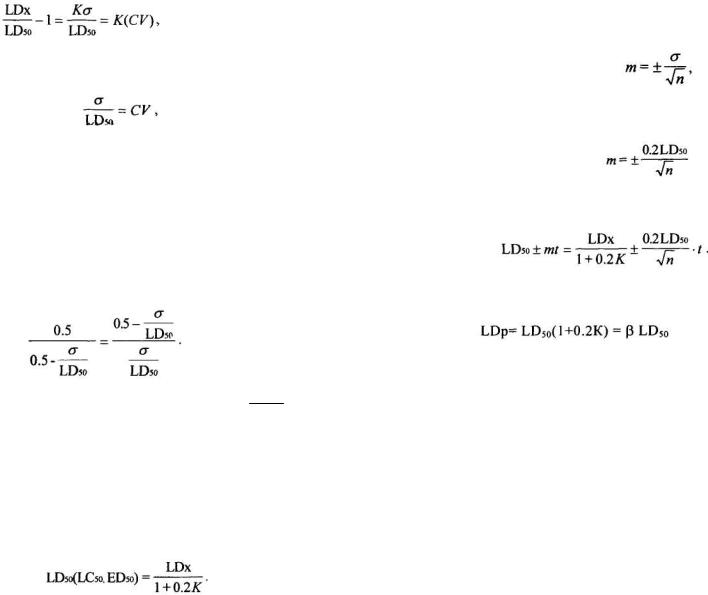
(2.79)
Для эффекта (Р), наблюдаемого в эксперименте для дозы LD, величина К однозначно определена. Поэтому в уравнении 2.79 два неизвестных: а и LD50. Однако отношение
(2.80)
т.е. коэффициент вариации, также может быть определено, исходя из следующих соображений.
По данным литературы (автор ссылается на Г.Ф.Лакина (1990)), максимальное значение коэффициента вариации для нормального распределения величин равно 0.5. Однако в реальных экспериментах CV часто бывает ниже этого уровня. Для оценки числового значения CV — используем правило «золотого сечения» отрезка протяженностью 0.5, раз-
бив его на два неравных отрезка: |
|
(меньший); (0.5 — |
|
) |
|
LD50 |
|
LD50 |
|
(больший). Тогда в соответствии с правилом «золотого сечения»:
(2.81)
Из этого условия получается, что меньшее значение , соответ-
LD50
ствующее принимаемому коэффициенту вариации, равно 0.19. Помимо указанной теоретически обоснованной величины (CV=0.19),
была проведена обработка опытных данных различных авторов. Были проанализированы значения CV для 289 веществ и установлено, что среднее значение равно 0.22. Выбирая среднее из двух выявленных значений (CV=0.19 и CV=0.22), примем для дальнейшего CV=0.20.
Введя CV=0.2 в уравнение 2.75, после преобразований получим окончательное уравнение для расчета LD50:
(2.82)
Уравнение (2.82) позволяет проводить расчет средних доз методом одной точки, определяя в эксперименте вероятность Р при дозе LDx (LCx, EDx). Для облегчения расчетов приводим табл. 8 приложения, содержащую значения К в зависимости от числа животных в группе и ко-
личества животных, у которых наблюдался изучаемый эффект.
Для расчета стандартной ошибки (т) величины LD50 (LC50, ED50) воспользуемся следующим соотношением:
(2.83)
где n — число животных в группе.
Так как в соответствии с установленным выше CV=0.2, то (2.79) преобразуется к виду:
. |
(2.84) |
Для расчета доверительных границ LD50(LC50, ED50) используем коэффициенты Стьюдента для уровня значимости 0.05 и числа степеней свободы f= п–1. Тогда получим:
(2.85)
Добавим к изложенному, что предложенный метод позволяет оценивать не только средние дозы, но и любые другие категории доз (LDp, LCp, EDp, EСp). Для этой цели уравнение (2.78) преобразуем к виду:
. |
(2.86) |
Для вероятностей эффекта (Р), равных 0.05, 0.16, 0.84, 0.95 и 0.99, числовые значения Р равны соответственно 0.67, 0.80, 1.20, 1.33 и 1.466.
Мы изложили данный метод в редакции, максимально приближенной к работе Г.Т.Фрумина (1991). В связи с этим, внимательные читатели смогли заметить некоторое несовпадение формулировок и понятий, что не затрагивает сущность данного метода. В этой же работе автор приводит доказательства точности метода на основе сравнения показателей токсичности, вычисленных по тем же исходным данным другими методами.
Исходя из канонов строгости, принятой в теории вероятностей, можно сразу же отметить недостатки метода Фрумина. Так, стержневым его моментом является максимальное значение коэффициента вариации для доказательства нормальности распределения функции эффективности. Но при этом не стоит забывать, что при нормальном распределении коэффициент вариации имеет не только критическое максимальное значение равное 0.33, вытекающее из уже приводимого выше правила «трех сигм», но и критическое минимальное значение, отражающее такой показатель как положительный эксцесс нормального распределения выборки. Для функции эффективности это свойство выражается в боль-
шом угле наклона к оси абсцисс. Кроме того, вызывает обоснованные |
Глава 3. Токсикометрические модели построения функции |
сомнения возможность применения вероятностного распределения |
эффективности и вычисления категорий эффективных доз |
Стьюдента как жесткой статистической характеристики к вычислению |
|
доверительных интервалов категорий эффективных доз по формулам |
В предыдущих главах были даны основные представления функции |
(2.85) и (2.86), в которых применено эмпирически найденное фиксиро- |
эффективности, приведены и проанализированы существующие (тради- |
ванное значение коэффициента вариации. Из приведенных доводов сле- |
ционные) методы ее построения и вычисления категорий эффективных |
дует, что метода Фрумина, так же как и другие методы, не решает про- |
доз. Единым принципом всех этих методов является первичное по- |
блемы «доза-эффект» для малого числа наблюдений. |
строение нормальной функции эффективности и вторичное вычисление |
Подводя итог анализу существующих методов расчета среднеэффек- |
категорий эффективных доз. При этом необходимо использовать опре- |
тивной дозы, отметим следующее. |
деленный способ планирования экспериментов, имеющий в своей осно- |
1. Все существующие методы расчета среднеэффективной дозы ис- |
ве оценку частоты эффекта в однородных группах тест-объектов, что не |
пользуют в качестве исходных данных значения частот эффектов, на- |
всегда оптимально, оправдано и допустимо в экспериментальной прак- |
блюдавшихся в однородных группах тест-объектов после испытания на |
тике. Современное развитие токсикометрии выдвигает практическую |
них заданных доз исследуемых веществ. Это предполагает предвари- |
необходимость разработки таких моделей вычисления категорий эф- |
тельное планирование токсикологического эксперимента для формиро- |
фективных доз и построения функции эффективности, которые бы не |
вания исходных данных. В практике часто встречаются случаи, когда |
предъявляли граничных условий к планированию токсикологического |
провести подбор однородных групп тест-объектов технически невоз- |
эксперимента, были бы статистически адекватными и позволяли бы по- |
можно в силу особенностей эксперимента. Поэтому на данном этапе пе- |
лучать надежные результаты с использованием минимально возможно- |
ред исследователями стоит проблема разработки таких статистических |
го числа тест-объектов. |
методов построения функции эффективности, которые могли бы ис- |
Оптимальным было бы создание таких моделей, которые позволяли |
пользовать а качестве исходных данных результаты независимых еди- |
бы строить функцию эффективности и вычислять категории эффектив- |
ничных испытаний, исключающих необходимость формирования од- |
ных доз непосредственно по исходным данным токсикологического |
нородных групп тест-объектов и вычисления в них частот проявления |
эксперимента без формирования каких-либо групп тест-объектов и без |
заданного признака. |
ограничения интервалов испытанных доз. Потребности токсикологиче- |
2. Существующие методы расчета среднеэффективной дозы основы- |
ского эксперимента устанавливают, чтобы в качестве исходных данных |
ваются на гипотезе о нормальном распределении функции эффективно- |
могли быть использованы результаты независимых единичных испыта- |
сти. Вместе с тем, способы статистического подтверждения этой гипо- |
ний. Поэтому целью данной главы и является решение указанных про- |
тезы для конкретных экспериментальных ситуаций до настоящего вре- |
блем. |
мени не разработаны. Поэтому требуется решить частную задачу оцен- |
Глава сформирована следующим образом. В первом разделе оп- |
ки вида распределения функции эффективности. |
ределяется алгоритм построения функции эффективности и вычисления |
3. При расчете среднеэффективной дозы до настоящего времени не |
категорий эффективных доз по результатам независимых единичных |
учитывается влияние погрешности исходных данных на результаты вы- |
испытаний в виде последовательного выполнения определенных этапов |
числений, что ставит их качество под сомнение. |
и статистических процедур, направленных на оценку достоверности и |
|
качества промежуточных и конечных результатов. Во втором разделе |
|
приведены методы оценки качества и пригодности полученных исход- |
|
ных данных для построения функции эффективности и вычисления ка- |
|
тегорий эффективных доз. Третий раздел посвящен разработке метода |
|
непараметрического вычисления категорий эффективных доз по резуль- |
|
татам независимых единичных испытаний. В нем заложен принцип не- |
|
зависимого вычисления отдельных категорий эффективных доз без |
предварительного построения и оценки вида распределения функции эффективности. В четвертом разделе приведен метод и критерии оценки нормальности распределения функции эффективности. В пятом разделе предложен метод оценки устойчивости среднеэффективной дозы, полученной по результатам независимых единичных испытаний на минимально возможном числе тест-объектов. В шестом разделе показана возможность параметрического построения нормальной функции эффективности при помощи метода максимального правдоподобия Фишера. В седьмом разделе определены в сравнительном плане возможности предлагаемого непараметрического метода вычисления категорий эффективных доз по результатам независимых единичных испытаний, в ходе которых заданные дозы измеряются с известной погрешностью
В целом, приведенные методы основываются на современных представлениях математической статистики и отвечают требованиям токсикометрии, что и послужило причиной их определения как токсикометрических.
3.1. Алгоритм построения функции эффективности и вычисления категорий эффективных доз по результатам независимых единичных испытаний
Для решения поставленной задачи проведем некоторые уточнения статистических и биологических понятий, касающихся зависимости «доза-эффект».
Результаты независимых единичных испытаний в токсикологическом эксперименте представлены в виде пар показателей «дозаэффект»: испытанной дозы и эффекта, проявившегося у тест-объекта и выраженного в альтернативной форме. Независимыми они являются потому, что при последующих вычислениях не включаются в состав ка- ких-либо однородных групп, а единичными — потому, что каждое наблюдение выступает как самостоятельный представитель экспериментальной выборки даже в случаях повторных испытаний.
Пусть X обозначает случайную величину или гипотетическую минимальную дозу, при воздействии которой у тест-объекта с полной вероятностью (абсолютно точно) проявился бы положительный эффект, например, летальный исход. Назовем эту дозу гипотетической минимальной абсолютно эффективной (летальной) дозой.
Обозначим через Y экспериментально испытанную дозу, а через W
— наблюдавшийся у тест-объекта эффект. С точки зрения теории вероятностей результаты токсикологического эксперимента состоят в том, что после испытания заданной дозы (Y) у тест-объекта проявится либо
положительный (W=l), либо отрицательный (W=0) эффект. При этом, если испытанная доза больше гипотетической (Y>Х), то регистрируется положительный эффект, и наоборот. Таким образом, показатель эффекта W служит индикатором событий (Y>X)
Биологическая сущность сказанного становится более понятной из следующих пояснений. Например, для каждого яда теоретически существует такая минимальная доза, которая вызывает у конкретного тестобъекта (животного) летальный эффект. Экспериментально определить эту дозу для каждого животного невозможно. Если животное в эксперименте выжило, то оно получило дозу яда заведомо меньшую минимальной абсолютно летальной дозы. И наоборот, в случае гибели, животное получило дозу яда заведомо большую минимальной абсолютно летальной дозы. Понятно, что для каждого животного эта доза будет различной, что определяется индивидуальной чувствительностью особей биологического вида к тестируемому препарату.
С точки зрения теории вероятностей минимальная абсолютно эффективная доза представляет собой случайную величину с функцией распределения:

Основываясь на принципах и критериях токсикометрических моделей, нами был разработан алгоритм построения функции эффективности исследуемых веществ по результатам независимых единичных испытаний (см. рис. 3.1).
Этот алгоритм включает последовательность выполнения математических операций в ходе построения функции эффективности токсичных веществ по результатам независимых единичных испытаний. Переход к каждому последующему шагу возможен только при условии выполнения предыдущего, что исключает возможность появления оши-
|
бок в конечных результатах вычисления категорий эффективных доз. |
|
3.2. Оценка зависимости «доза-эффект» |
|
На первом этапе решения задачи вычисления среднеэффективной до- |
|
зы мы сразу же сталкиваемся с проблемой определения минимального |
|
объема экспериментальной выборки, которая обеспечила бы необходи- |
|
мую надежность результатов вычислений. Рассмотрим теоретические |
|
положения, на основании которых возможен обоснованный выбор ми- |
|
нимального числа наблюдений для построения функции эффективности |
|
и вычисления надежных категорий эффективных доз. |
|
Так как функция эффективности задана в определенном диапазоне |
|
доз, то для ее построения необходимо произвести экспериментальную |
|
выборку именно из этого диапазона. Несомненно, что в таком диапазо- |
«парадоксальности», увеличение вводимой дозы приводит к |
не при увеличении доз у тест-объектов должно наблюдаться достовер- |
уменьшению эффекта. |
ное увеличение эффекта, т.е. необходимо доказать статистическую зна- |
чимость влияния испытанных доз на результативный признак. Применять параметрические методы статистического анализа для решения поставленной задачи не представляется возможным, по той причине, что на данном этапе построения функции эффективности ее распределение неизвестно.
Проведенный анализ непараметрических методов позволил установить, что для оценки значимости зависимости «доза-эффект» оптимальным является критерий U Вилкоксона-Манна-Уитни (Гублер Е.В., Генкин А.А., 1973; Тарасенко Ф.П., 1976; Гублер Е.В., 1978). Этот критерий является мощным непараметрическим критерием, позволяющим выявлять различия в средних для независимых выборок, что подходит для решения задачи оценки достоверности смещения в средних тенденциях доз, вызвавших положительные или отрицательные эффекты.
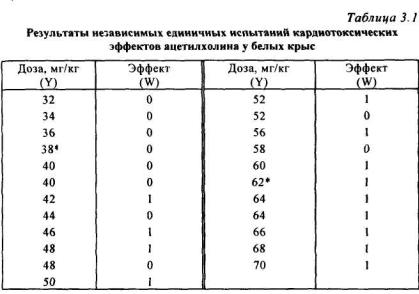
Сущность применения критерия U Вилкоксона-Манна-Уитни заключается в составлении общего упорядоченного ряда данных двух выборок. Возьмем в качестве примера независимых единичных испытаний результаты собственных исследований на белых крысах кардиотоксических эффектов ацетилхолина (см.табл.3.1). Совершенно очевидно, что такого типа исходные данные непригодны для расчета среднеэффективной дозы ни по одному из общепринятых методов.
превышают дозы, не вызвавшие эффекта. В приведенном примере в роли первой выборки выступают значения доз, вызвавшие отрицательные эффекты, а в роли второй выборки — значения доз, вызвавших положительные эффекты. Пример формирования двух таких выборок приведен в табл. 3.2. Далее подсчитывается число нарушений расположения чисел одного ряда по сравнению с числами другого ряда (инверсии). Одним нарушением, или инверсией, считается такое расположение числа, при котором перед каким-либо числом первого столбца стоит одно число второго столбца. Если перед каким-либо числом первого столбца стоят два числа второго столбца, то это считается как две инверсии и т.д. Число инверсий обозначается через U. Если в упорядоченном ряду встречаются повторяющиеся цифры, то подсчет инверсий следует соотносить с задачами эксперимента и формулировкой статистической гипотезы.
В данном случае необходимо проверить гипотезу о том, что в средних тенденциях дозы, вызвавшие положительные эффекты достоверно
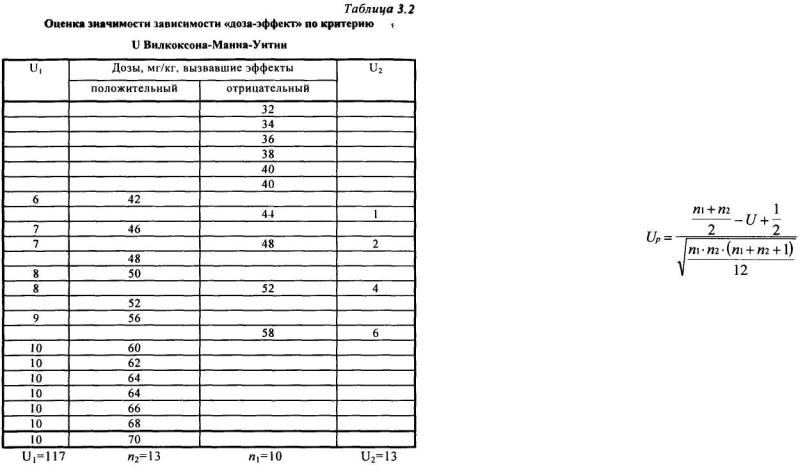
Так, в данном случае требуется проверить гипотезу о том, что в средних тенденциях дозы, вызвавшие положительный эффект, достоверно отличаются от доз, не вызвавших эффекта, то целесообразно и статистически обосновано будет применение двухстороннего критерия, а повторяющиеся значения в двух выборках необходимо располагать таким образом, чтобы получалось минимальное число инверсий.
В упорядоченном ряду инверсии могут быть подсчитаны двумя способами: относительно первой и относительно второй выборки (столбца). Следует выбрать тот способ, который дает меньшую сумму инверсий. В приведенном примере U1=117, U2=13. Поэтому в качестве показателя числа инверсий выбирается значение 13. Дальнейшая работа состоит в сравнении полученного числа инверсий с табличными данными.
В табл. 9 приложения приведены максимальные значения числа инверсий U, при которых различие между двумя выборками следует считать значимым с вероятностью Рu=0.05. Для выбранного примера вычисленное число инверсий составило 13 при n1=10 и п2=13, что не меньше критического значения, взятого из табл. 9 приложения при Р=0.05 (Uтабл=37) (Гублер Е.В., 1978). Следовательно, гипотеза о значимости зависимости «доза-эффект» в исследованном диапазоне доз считается статистически доказанной.
В том случае, если число наблюдений в одной или в двух группах превышает 20, то после подсчета числа инверсий можно вычислить вероятность различий двух выборок Up по формуле 3.3, используя свойства нормального распределения:
(3.3)
Если Up≥1.96, то с вероятностью ошибки Р≤0.05 можно утверждать о различиях эффектов в двух сравниваемых выборках.
Анализируя критическое значение числа инверсий, можно заметить, что оно значительно превышает вычисленное значение. Кроме того, крайние значения выборки не влияют на результаты подсчета числа инверсий, а имеют значение только для поиска критического числа наблюдений. Поэтому, исключая крайние значения, можно выбрать минимальный диапазон испытанных доз, в котором сохраняется заданная значимость различий числа инверсий, т.е. сохраняется зависимость «до- за-эффект». При исключении крайних значений необходимо придерживаться приблизительного равенства доз, при испытании которых наблюдались как положительные, так и отрицательные эффекты, т.е. п1≈п2. Для приведенного в табл. 3.1 случая, минимальный диапазон испытанных доз, в котором наблюдается значимая зависимость «доза-
эффект», ограничивается дозами 38...62 мг/кг (n1=7, n2=8, Uтабл=13 при Р=0.05). Этот минимально значимый диапазон включает 15 испытанных
доз. Тем самым проведено доказательство того факта, что при возрастании испытанных доз достоверно увеличиваются наблюдаемые эффекты. Это является основанием для построения функции эффективности по полученным исходным данным.
Предлагаемый нами методический подход имеет логический смысл и статистическое обоснование. Кроме того, он применим и в тех случаев, когда повторно испытываются одинаковые дозы и формируются одно-
