
4 курс / Общая токсикология (доп.) / Токсикометрия эффективных доз
.pdf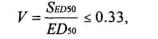
вестными распределениями, имеющими S-образный вид или приводящимися к линейному виду путем соответствующих преобразований (Антомонов М.Ю., Русаков Л.Т., 1988; Антомонов М.Ю., 1991; Антомо-
нов М.Ю., Богорад B.C., 1992).
В некоторых случаях кривая «доза-эффект» вообще не может быть аппроксимирована ни одним из распределений. Экспериментально установлены бимодальные и даже полимодальные кривые «доза-эффект». Такого рода эффекты получили название парадоксальных и были выделены в отдельную общебиологическую проблему (Саркисов Д.С. и соавт., 1969). Многие авторы полагают и доказывают, что парадоксальные эффекты не являются случайными, а имеют широкое распространение в биохимии и физиологии многих живых систем в самых разнообразных условиях и что их практическая и теоретическая значимость не была еще полностью осознана и оценена.
Статистические методы доказательства парадоксальности функции эффективности до настоящего времени не предложены.
Рассмотрим еще один вопрос, относящийся к оценке вида распределения функции эффективности. Согласно закону нормального распределения, соотношение величин ED50 и SED50 имеют строго определенные границы. Так, например, коэффициент вариации, найденный по формуле:
не может превышать 0.33 (33%). В противном случае нарушается правило «трех сигм», как одно из фундаментальных положений теории вероятностей. Правило «трех сигм» вытекает из того положения, что трехсигмовые границы принимаются за границы практически предельных возможных значений нормально распределенной случайной величины. Если случайная величина имеет нормальное распределение, то отклонение этой величины от математического ожидания по абсолютной величине не превосходит утроенного среднего квадратического отклонения с вероятностью Р = 0,0025 (Герасимович А.И., 1983). На этом основании по данному критерию можно косвенно определить соответствие любой случайной величины, и, в частности, функции эффективности, нормальному закону. Так, в работе Е.Н.Львовского (1982) прямо указывается, что если коэффициент вариации превосходит значение 33%, то распределение случайной величины, определенное по совокупности экспериментальных наблюдений, отличается от нормального закона.
Следует различать два понятия: распределение категорий эффектив-
ных доз и распределение функции эффективности. Распределение отдельных категорий эффективных доз от ED1 до ED99 всегда соответствует нормальному закону, исходя из центральной предельной теоремы (Венецкий И.Г., Венецкая В.И., 1979), поскольку они отражают частоту появления эффекта в отдельной точке. Например, если при испытании какой-либо дозы яда на группе тест-объектов наблюдался эффект в 2 случаях из 10, то явно такая доза будет иметь категорию ED20, так как частота появления эффекта в экспериментальной группе составляет 20%. Совершенно очевидно, что количественное выражение эффекта имеет биномиальное распределение, которое переходит в нормальное при увеличении числа наблюдений, если число эффектов в группе пропорционально увеличивается (Венецкий И.Г., Венецкая В.И., 1979).
Поэтому есть основания считать, что в данном случае распределение ED20 близко к нормальному распределению.
Вид распределения функции эффективности, как уже было сказано, имеет принципиальное значение и должен быть установлен в каждом конкретном случае. Однако, удовлетворительных критериев оценки нормальности функции эффективности до настоящего времени не предложено. Этот факт затрудняет решение главного вопроса о возможности и корректности построения функции эффективности и вычислении значений среднеэффективной дозы и других категорий эффективных доз при помощи традиционных методов. При их использовании нормальное распределение функции эффективности предполагается априори, что не исключает возможности ошибок.
1.3. Исходные данные для построения функции эффективности
Каждый метод построения функции эффективности предъявляет определенные требования к виду исходных данных, а, соответственно, и к способу планирования биологического эксперимента. Существующие статистические методы позволяют вычислять значение среднеэффективной дозы и доверительные интервалы для нее с заданным уровнем вероятности. Проведем статистический анализ традиционных способов планирования экспериментов и требований к исходным данным для расчета среднеэффективной дозы.
Разработанные к настоящему времени методы расчета среднеэффективной дозы предполагают первоначальное формирование по результатам эксперимента матрицы исходных данных в виде пар показателей, включающих воздействовавшие на однородные группы тест-объектов дозы и наблюдавшиеся в этих группах частоты эффектов. Вопрос о вы-
полнении минимального числа экспериментов для построения надежных статистически обоснованных оценок конечных показателей является предметом научных дискуссий до настоящего времени. Считается, что для нахождения среднеэффективной дозы следует поставить опыты с несколькими (не менее трех) группами тест-объектов (как правило, не менее шести в каждой группе) при разных дозах (Беленький М.Л., 1963). При этом некоторые авторы рекомендуют (Finney D.J., 1979), а другие предлагают вообще не использовать 0 и 100% эффекты (Miller L.S., Tainter M.L., 1944) и доказывают, что достаточным условием для расчета ED50 является наличие не более трех испытанных доз по шесть тест-объектов в группах. Кроме того, испытуемые дозы должны соответствовать логарифмической шкале измерений, что является необходимым условием для последующего применения некоторых методов расчета среднеэффективной дозы. Из этого следует, что существующие (традиционные) методы расчета среднеэффективной дозы выдвигают граничные условия не только в отношении количества исходных данных, но и в отношении их структуры.
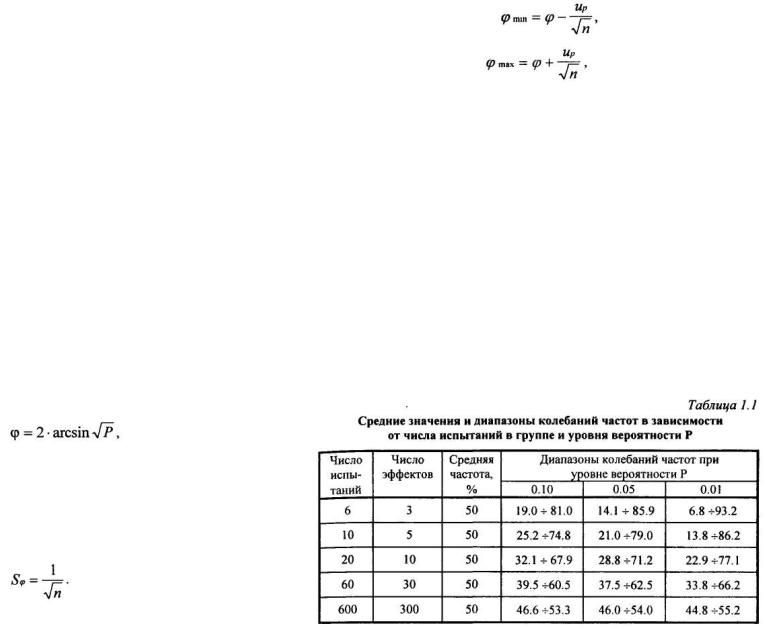
Рассмотрим обоснованность указанных граничных условий с точки зрения теории вероятностей. Известно, что частоты эффектов, выраженные в процентах, имеют погрешность, зависящую от числа наблюдений. Количественно определить значения погрешностей частот эффектов возможно только после их предварительного преобразования, так как сами проценты имеют распределение, далекое от нормального. При любом числе наблюдений вычислить доверительные интервалы процентов возможно по методу углового преобразования Фишера:
(1.10)
где Р — частота, выражаемая в долях единицы.
Величина φ выражается в радианах и ее распределение близко к нормальному (Гублер Е.В., 1978). Поэтому угловое преобразование процентов эффектов по методу Фишера позволяет применять параметрические методы для вычисления доверительных интервалов. Если величина φ вычисляется в радианах, то она при n→∞ имеет среднеквадратическое отклонение, которое зависит только от числа наблюдений:
(1.11)
Доверительные интервалы для процентов при заданных уровнях вероятности Р вычисляются путем преобразования процентов в радианы по формуле (1.10) с последующим вычислением верхней и нижней границ по формулам (1.12) и (1.13):
(1.12)
(1.13)
где иp — квантиль функции нормального распределения.
Обратное преобразование радиан в проценты приводит к значениям границ искомого доверительного интервала.
В табл. 1.1 приведены вычисленные нами средние значения и доверительные интервалы частот при разных уровнях вероятности Р, в зависимости от числа испытаний в группе.
Анализ результатов вычислений показывает, что сходимость к среднему значению частот с увеличением числа наблюдений в группах происходит довольно медленно. Так, при числе наблюдений в группе равном 20 и уровне вероятности Р = 0.05 колебания от среднего значения в большую и меньшую сторону составляют более 20%. Очевидно, что в подобных случаях имеет место большая неопределенность показателей, которая существенно сказывается на точности конечного результата. Следует отметить, что погрешность вычислений, возникающая по указанной причине, никак не учитывается в существующих в настоящее время методах расчета среднеэффективной дозы. На проблему величины выборки для оценки динамики частотных показателей обращают внимание некоторые авторы (Минченко В.А. и соавт., 1986 и др.).
Рассмотрим еще одну проблему, имеющую отношение к планированию токсикологического эксперимента, на существования которой исследователи часто не обращают внимание. Это проблема статистиче-

ской оценки значимости влияния изучаемого фактора (дозы) на результативный признак (эффект). Не вызывает сомнения тот очевидный факт, что проводить какие-либо количественные оценки зависимости «дозаэффект» возможно только в том случае, если статистически доказана значимость влияния испытанных в эксперименте доз на результативный признак. Отметим, что исследование зависимости «доза-эффект» может рассматриваться как частный случай факторного анализа. Так как в зависимости «доза-эффект» результативный признак выражен в альтернативной форме, то количественно оценить силу и значимость влияния испытанных доз на проявившиеся эффекты позволяет однофакторный дисперсионный анализ для качественных (альтернативных) признаков.
Оценим адекватность приведенных в начале данного раздела общепринятых требований к планированию эксперимента для определения среднеэффективной дозы с позиций однофакторного дисперсионного анализа для альтернативных признаков. Сущность этого статистического метода заключается в следующем (Мерков A.M., Поляков Л.Е., 1974).

Показатели fx и fZ представляют собой степени свободы для соответствующих дисперсий и используются при сравнении вычисленного значения Fx с критическим (табличным) значением при заданном уровне вероятности (см. табл. 2 приложения). Они рассчитываются по формулам:
(1.25 и 1.26)
где r х — число градаций фактора.
Проведем по методу однофакторного дисперсионного анализа оценку значимости влияния испытанных доз на результативный признак при общепринятом планировании эксперимента и получении после его выполнения оптимальных исходных данных в виде трех групп наблюдений (см.табл. 1.2). Вычисленные значения показателей однофакторного дисперсионного анализа составили: Сγ = 4.50; Сх = 1.33; Cz = 3.17; η2x=29,6%; η2z= 70.4 Fx=3.14. Критическое значение критерия Фишера для уровня вероятности Р = 0.05 и степеней свободы fх = 2, fz=15 согласно таблиц распределения Фишера равно 3.68 (см. табл.2 приложения). Так как вычисленное значение Fx оказалось меньше критического, то при указанном уровне вероятности Р влияние испытанных доз на результативный признак статистически не доказано. Формально, построение функции эффективности по полученным исходным данным и последующий расчет категорий эффективных доз по сгруппированным исходным данным с использованием традиционных методов нельзя считать статистически обоснованным.
Таким образом, с позиций однофакторного дисперсионного анализа для данного случая показано, что общепринятое планирование эксперимента по определению среднеэффективной дозы, согласно которому считается достаточным получение исходных данных на трех группах численностью по 6 тест-объектов в каждой, нельзя признать статистически обоснованным. Даже при оптимальных результатах испытаний в группах тест-объектов гипотеза о значимости влияния испытанных доз на результативный признак не имеет статистического подтверждения. Определять вероятности эффектов в группах, и строить на их основе модели оценки функции эффективности при помощи регрессионного анализа весьма сомнительно. В данном и в подобных случаях необходимо увеличивать число испытаний в группах. Например, при увеличении числа тест-объектов в группах до 7, и при исходе испытаний в группах 1/7, 3/7 и 6/7 соответственно, вычисленные значения показателей однофакторного дисперсионного анализа составили: Сγ=5.24; Сх=1.81; CZ=3.43; η2X =34.55%; η2z =65.45%, Fx=4.75. Критическое значение ста-
тистики Фишера для уровня вероятности Р=0.05 и степеней свободы fx=2, fz=18 согласно таблиц распределения Фишера равно 3.55. Так как вычисленное значение Fx превышает критическое для заданного уровня вероятности, то вывод о значимости влияния испытанных доз на результативный признак считается статистически обоснованным. Это является основанием для построения функции эффективности и последующего расчета среднеэффективной и других категорий эффективных доз.
В экспериментальной практике часто встречаются ситуации, при которых невозможно осуществить предварительное планирование и последующее выполнение эксперимента для получения исходных данных, пригодных к использованию в традиционных методах расчета средне-
эффективной дозы. Если, например, по каким-либо причинам невозможно сформировать однородные группы с требуемым числом тестобъектов, то для расчета среднеэффективной дозы по такого рода исходным данным в практике приходилось вынужденно пользоваться следующим методическим приемом. Весь диапазон испытанных доз по произвольно выбранным критериям разбивается на поддиапазоны. В каждом поддиапазоне определяется частота появления эффекта. Середины поддиапазонов и вычисленные частоты эффектов принимаются в качестве исходных данных для расчета среднеэффективной дозы
Следует отметить, что при реализации данного методического подхода к расчету среднеэффективной дозы по нестандартным исходным данным имеет место дополнительная погрешность конечного результата, обусловленная группировкой или разбиением испытанных доз на поддиапазоны. Оценить эту погрешность количественно обычно не представляется возможным. Поэтому точность расчетного показателя в таких случаях является иллюзорной и статистически не обоснованной.
Существующие на современном этапе представления о планировании токсикологического эксперимента для определения среднеэффективной дозы можно выразить следующим образом. Эффективная доза представляет собой статистический показатель, вычисляемый по экспериментальным исходным данным, включающим испытанные на тестобъектах дозы и соответствующие им частоты появления в группах регистрируемого эффекта. Характер и структура исходных данных определяется способом последующего статистического вычисления среднеэффективной дозы и других категорий эффективных доз. Традиционные методы расчета среднеэффективной дозы предъявляют к исходным данным определенные требования как в отношении числа тест-объектов в группах, так и в отношении интервалов испытанных доз. Оптимальным следует признать тот способ расчета искомых показателей, который предъявляет минимальные граничные условия к структуре исходных данных.
Проводить статистические вычисления по экспериментальным данным возможно только в том случае, если доказана значимость влияния испытанных доз на проявившиеся у тест-объектов эффекты.
Категории эффективных доз и соответствующие им вероятности эффектов определяют в двумерной системе координат кривую «дозаэффект» или функцию эффективности, отражающую биологическую сущность взаимодействия исследуемого фактора в заданной дозе с тестобъектом. Функция эффективности для большинства известных токсикантов и стандартных условий эксперимента имеет S-образный вид, и
может быть аппроксимирована одним из известных распределений. Расчет среднеэффективной дозы возможен в том случае, если функ-
ция эффективности соответствует известному закону распределения (нормальному или логарифмически нормальному). В некоторых случаях функция эффективности может быть бимодальной и даже полимодальной. Статистический анализ в этом случае затруднен или вообще невозможен по причине отсутствия соответствующих статистических методов.
Таким образом, изложенный в данной главе материал позволяет получить целостное представление об основных аспектах проблемы расчета эффективных доз. Эффективные дозы являются статистическими величинами и подчиняются законам теории вероятностей и математической статистики. Всякое отступление от этих законов может привести к необоснованным и некорректным результатам вычислений.
Имея необходимые представления о функции эффективности и категориях эффективных доз как статистических величинах, проведем анализ существующих (традиционных) методов расчета среднеэффективной дозы с позиций современных представлений теории вероятностей и математической статистики.
2.Анализ методов расчета эффективных доз с позиций теории вероятностей и математической статистики
Методы математического анализа зависимости «доза-эффект» разрабатывались и совершенствовались наряду с развитием методов математической статистики. Отражением определенных этапов этого развития являются различные методы расчета эффективных доз. Без их теоретического анализа и осмысления невозможен дальнейший прогресс в решении данной проблемы Поэтому мы посчитали необходимым привести наиболее известные методы расчета значений среднеэффективной дозы (по возможности в редакции самих авторов) и дать их анализ с позиций современных представлений токсикометрии, математической статистики и теории вероятностей. Сразу отметим, что в редакции некоторых авторов возможны отдельные неточности в формулировках понятий, которые мы умышленно не корректировали. Мы думаем, что это не помешает читателям самим разобраться в сути приведенных методов.
2.1. Метод Беренса Метод Беренса был опубликован в 1929 году и явился по сути первой
серьезной работой по проблеме количественной оценки зависимости
«доза-эффект». Метод основан на приеме «накопления частот», который заключается в том, что к числу положительных исходов испытаний в каждой большей градации (дозы) прибавляется число положительных исходов во всех меньших градациях и, наоборот, к числу отрицательных исходов испытаний в каждой меньшей градации прибавляется число отрицательный исходов во всех больших градациях фактора. Теоретически этот прием имеет определенный смысл. Например, если у тестобъекта учитываемый эффект проявился при малой дозе препарата, то несомненно, этот же эффект у данного тест-объекта проявился бы и при всех больших дозах. И наоборот, если у тест-объекта эффект отсутствовал при больших дозах, то при всех меньших дозах у того же тестобъекта ожидать эффекта не приходится. Конечно, это допущение справедливо только для веществ, не обладающих парадоксальным действием на тест-объекты. На основании испытанных доз и «накопленных частот» графически строится функция, из которой и определяется значение среднеэффективной дозы. Кроме того, рассчитать значение среднеэффективной дозы возможно и не прибегая к построению графика, а используя методы линейной интерполяции.
Применение метода Беренса выдвигает граничные условия равенства интервалов между градациями фактора (дозами) и равенства числа тестобъектов в каждой группе, а также симметричность кривой «дозаэффект» относительно ее середины, что обусловлено нормальностью распределения функции эффективности.
Отношение исследователей к методу Беренса, а точнее к приему «накопления частот» не было однозначным. Так, В.М.Карасик (1944) поддерживал и пропагандировал данный метод. Вместе с тем М.Л.Беленький (1963) отмечал, что в процессе «накопления частот» искусственно преувеличивается «вес» крайних вариантов индивидуальной чувствительности животных к изучаемому веществу, вследствие чего процент смертельных исходов от малых доз оказывается заниженным, а от высоких доз — завышенным. Таким образом, прием «накопления частот» ведет к искажению формы «характеристической кривой» (функции эффективности. Очевидно, однако, что средний участок кривой при этом не искажается и, следовательно, в значение LD50 не вносится большой ошибки. Само собой разумеется, что по изложенной причине метод Беренса не пригоден для нахождения доз, вызывающих другие частоты смертельных исходов (например LD10 и LD9o). Эти доводы вполне убедительны, и поэтому еще раз отметим, что метод Беренса пригоден только для определения значения среднеэффективной дозы, но не других категорий эффективных доз.
Вычисление приближенного значения стандартной ошибки SXED50 при применении метода Беренса предложено позднее Гэддамом в 1933 году. В результате экспериментального изучения распределения минимальных эффективных доз была найдена следующая эмпирическая формула (Беленький М.Л., 1963):
(2.1)
где S — среднее квадратическое отклонение, которое находится из графика «доза-эффект» и равно половине разности ED84 - ED16 ); d — интервал между испытанными дозами; к — постоянный множитель равный 0.66.
Анализируя метод Беренса можно отметить, что он не имеет достаточного статистического обоснования, а основывается на условных эмпирических допущениях. На начальном этапе развития токсикометрии применение метода Беренса было допустимым и оправданным. В настоящее время его можно рассматривать только в историческом и познавательном плане.
2.2. Метод Рида и Менча
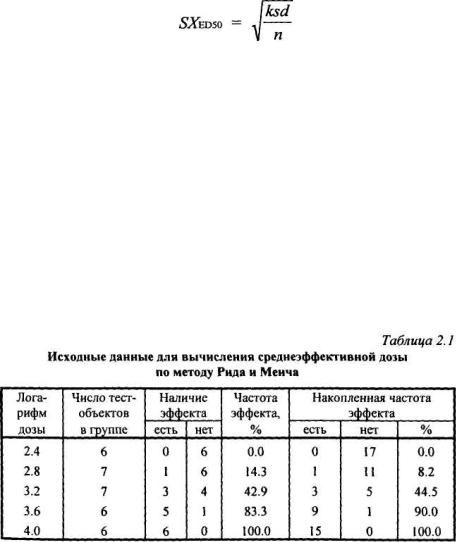
Метод Рида и Менча является одним из простейших методов вычисления среднеэффективной дозы. Порядок его использования приведен в работе В.Ю.Урбаха (1975), по которой мы определим его сущность на конкретном экспериментальном примере табл. 2.1.
Этот метод исходит из того естественного допущения, принятого в методе Беренса, что если некоторый тест-объект дал положительный эффект при какой-либо дозе, то он дал бы такой же эффект и при более

высоких дозах, и наоборот, если тест-объект дал отрицательный эффект при определенной дозе, то он дал бы также отрицательный эффект и при всех меньших дозах. Для правильного использования метода Рида и Менча необходимо, чтобы интервал между испытанными дозами был постоянным (в обычном или логарифмическом масштабе). Среднеэффективная доза применительно к исходным данным, приведенным в табл. 2.1, вычисляется по формуле:
где А — скорректированный процент положительных ответов, ближайший к 50% снизу; В — скорректированный процент положительных ответов, ближайший к 50% сверху; lВ-lА — соответствующие дозы.
Стандартная ошибка среднеэффективной дозы находится из формулы:
где к — число испытанных доз; h — интервал между испытанными
дозами; l75-l25 – дозы ED75 и ED25, которые находятся по методу линейной интерполяции.
Доверительные интервалы среднеэффективной дозы можно найти из соотношения:
(2.4)
Для примера, приведенного в табл. 2.1, логарифм среднеэффектив-
ной дозы равен 3.27 (0.89÷3.54).
Методу Рида и Менча присущи те же недостатки, что и методу Беренса. В нем больше эмпирических допущений, нежели ссылок на законы математической статистики. В этом методе реализуется способ линейной интерполяции внутри заданного диапазона доз.
2.3. Метод Кербера
В 1931 году Кербер предложил вычислять среднеэффективную дозу по формуле (Беленький М.Л., 1963):
(2.5)
где ED100 — доза препарата, которая вызвала эффект у всех тестобъектов в группе; d — интервал между двумя смежными дозами; z — среднее арифметическое из двух значений числа тест-объектов, у кото-
рых проявился положительный эффект при воздействии каждой из двух смежных доз, т — число тест-объектов в группе.
Метод Кербера, также как и метод Беренса, основывается на равенстве сумм площадей, ограниченных кривой «доза-эффект» справа и слева от среднеэффективной дозы, и последующем вычислении сумм площадей прямоугольных трапеций, что реализовано в формуле (2.2). Правильное использование данного метода предполагает одинаковое число тест-объектов в группах, но не менее 6 в каждой Интервал между смежными дозами не обязательно должен быть одинаковым. Кроме того, обязательно наличие дозы, вызвавшей 100% эффект в группе тестобъектов.
Используя формулу Гэддама (2.1) можно вычислить значение стандартной ошибки среднеэффективной дозы, определенной по методу Кербера. При этом значение постоянного множителя к принимается равным 0.564.
Метод Кербера в последствии подвергся серьезной критике. Прежде всего это широкий диапазон доз, включающий 0 и 100% эффекты Замена площади, ограниченной кривой «доза-эффект», на сумму площадей трапеций сказывается на точности вычислений среднеэффективной дозы. Значительно снижает точность вычислений неопределенность значения дозы, вызывающей 100% эффект, так как эта доза не имеет четкого биологического и статистического смысла
Нет сомнения в том, что метод Кербера, также как и метод Беренса, относится к разряду эмпирических методов с присущими ему недостатками, и также имеет только историческое значение.
2.4. Метод Першина
Первое упоминание о новом методе расчета среднеэффективной дозы Г.Н.Першин делает в 1939 году (Першин Г.Н., 1939). И только в 1950 году дается полное изложение метода (Першин Г.Н., 1950).
Смысл метода Першина заключается в вычислении интеграла функции по площадям прямоугольных трапеций, ограниченными смежными дозами и соответствующими частотами эффектов. Если эффекты выразить в процентах, то среднеэффективная доза может быть вычислена по формуле:
где а и b — значения смежных доз; т и п — соответствующие им
проценты эффектов в группах.
При исследовании токсичных веществ Г.Н.Першин впервые предложил использовать дозы, увеличенные в геометрической прогрессии и, в частности, пользоваться рядом Фульда, который представляет собой геометрические прогрессии с начальным членом 10n и знаменателем
m10 , где n — любое целое положительное или отрицательное число; m
–любое положительное число, отличное от нуля. Эти значения подбираются в соответствии с размахом доз.
Метод Першина, также как и предыдущие, предполагает симметричность кривой «доза-эффект», т.е. ее нормальность и определение на всем участке. Существенным недостатком метода является невозможность определения стандартной ошибки среднеэффективной дозы и ее доверительных интервалов.
2.5.Метод Беренса и Шлоссера
Метод Беренса и Шлоссера был предложен в 1957 году. Сущность данного метода и примеры его применения изложены в работе М.Л.Беленького (1963), Проанализируем по данной работе основные положения метода Беренса и Шлоссера.
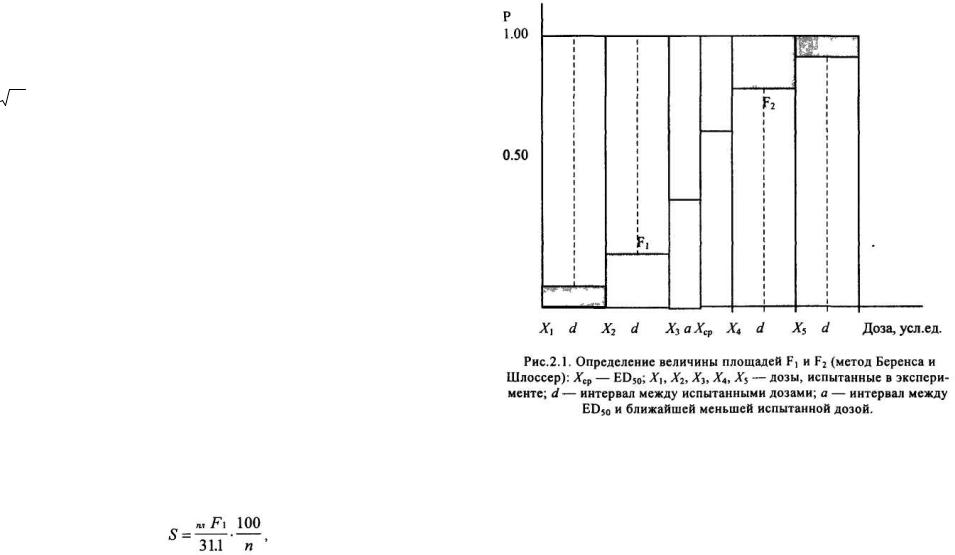
Принципиальным основанием этого метода, также как и описанного в 1929 году метода Беренса, является нахождение такого положения точки х на оси абсцисс, при котором пл.F1 = пл.F2 (см. рис. 2.1). Очевидно, что чем более крутой наклон имеет «характеристическая кривая» (функция эффективности), тем меньшей будет величина пл.F1 = пл.F2. Это обстоятельство позволяет, исходя из величины пл.F1 = пл.F2, вычислить «стандарт распределения S» (среднее квадратическое отклонение), значение которого дает возможность найти величину стандартной ошибки (SED50). Беренс и Шлоссер на основании анализа «характеристической кривой» нашли, что:
(2.7)
где п — количество животных, на которых испытывалась каждая доза изучаемого вещества.
При использовании метода Беренса и Шлоссера предпочтительно так планировать эксперимент, чтобы интервал между дозами сохранялся постоянным. Это значительно упрощает обработку результатов наблюдения.
Теоретически площади F1 и F2 являются пределами, к которым стремятся суммы площадей прямоугольников, имеющих своими основаниями бесконечно малые интервалы между испытываемыми дозами, а высотами — соответствующие этим дозам количества животных, у которых наблюдался (для пл.F2) или не наблюдался (для пл.F1) изучаемый признак.
Первой операцией при обработке экспериментального материала по методу Беренса и Шлоссера является вычисление предположительных эффектов от доз, соответствующих центральному значению интервалов между фактически испытанными дозами. Эти предположительные эффекты вычисляются путем нахождения средних арифметических между
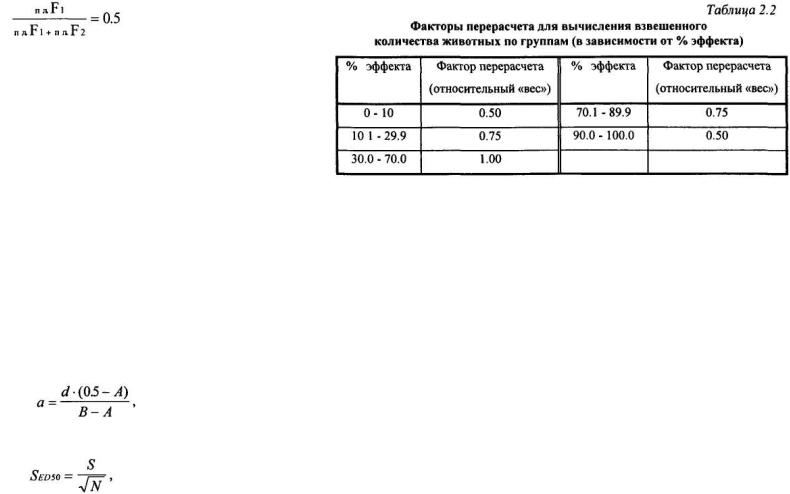
эффектами каждых из двух смежных доз, фактически испытанных в эксперименте. Задачу определения величины ED50 можно свести к задаче нахождения такого положения точки х на оси абсцисс, при котором справедливо соотношение:
(2.8)
На этом основании требуется найти наибольшую из испытанных доз, для которой отношение:
 ,
,
и наименьшую из испытанных доз, для которой отношение:
 .
.
Площадь каждого из прямоугольников, из которых складываются площади F1 и F2, является произведением его основания на высоту. Так как основания всех прямоугольников (интервалы между испытанными дозами) являются одинаковыми и входят в качестве множителей и в числитель, и в знаменатель вычисляемых отношений, то при определении А и В основания прямоугольников можно в расчет не включать.
Так как ED50 находится между величинами А и В, то ее значение можно вычислить из соотношения:
ED50 = А + а, (2.9)
где а — величина, меньшая, чем интервал d между испытанными дозами.
Величину а определяют путем прямолинейного интерполирования:
(2.10)
Для вычисления стандартной ошибки ED50 Беренс и Шлоссер предложили пользоваться формулой:
(2.11)
где N — общее количество животных, использованных в эксперименте, «взвешенное» по группам в зависимости от процента эффекта, наблюдавшегося в каждой группе животных.
Задача «взвешивания» заключается в том, чтобы придать большее значение (больший «вес») тем группам животных, в которых эффект приближается к 50%. Для вычисления величины N суммируют произве-
дения из фактического количества животных в каждой группе на фактор пересчета, соответствующий относительному «весу» животных данной группы. Эти факторы пересчета приведены в табл. 2.2 (Белень-
кий М.Л., 1963).
Относительный «вес» животных, входящих в группы, в которых процент эффекта равен 0 или 100, принимается равным нулю, и, следовательно, в величину N эти животные вовсе не входят.
Доверительные интервалы ED50 можно найти, определив значение t критерия Стьюдента при числе степеней свободы f = N - 1 и при заданном уровне вероятности Р (см. табл. 1 приложения).
Анализируя метод Беренса и Шлоссера становится совершенно ясно, что он основывается в большей степени на законах геометрии, чем на законах математической статистики.
Нет сомнения в том, что метод Беренса и Шлоссера, так же как предыдущие методы, представляет только исторический и познавательный интерес.
2.6. Пробит-анализ
Появление пробит-анализа следует рассматривать как существенный прогресс в решении проблемы расчета среднеэффективных доз. Его принципы используются во многих существующих до настоящего времени методах расчета среднеэффективной дозы.
Пробит-анализ прошел долгий путь совершенствования в работах многих авторов (Бессмертных Б.С., Акатов А.К., 1959; Прозоровский В.Б., 1962; Беленький М.Л., 1963; Лившиц П.З., 1966; Zbinden G., FluryRoversi M., 1981). Его разные модификации реализованы в ряде компьютерных программ для практического применения (Russell R.W. et al., 1977; Robertson J.L., et al., 1981; Schoofs G.M., Willhite C.C., 1984; Abou-
Setta M.M. et al., 1986; Laara E., 1987). Поэтому мы постараемся провес-
ти детальное обсуждение основных статистических положений пробитанализа.
2.6.1. Сущность пробит-анализа
Поиски оптимальных решений проблемы расчета среднеэффективной дозы привели Гэддэма (1933) к идее выравнивания кривой «дозаэффект» и ее преобразования в прямую линию, в основном, с целью визуализации данных и упрощения вычислительных операций. Пройдя определенные этапы совершенствования, этот методический подход является основным и до настоящего времени. В его основу положено предположение о нормальном распределении функции эффективности.
Согласно этому предположению, любое значение эффективной дозы х на оси абсцисс можно выразить через нормированное отклонение t:
(2.12)
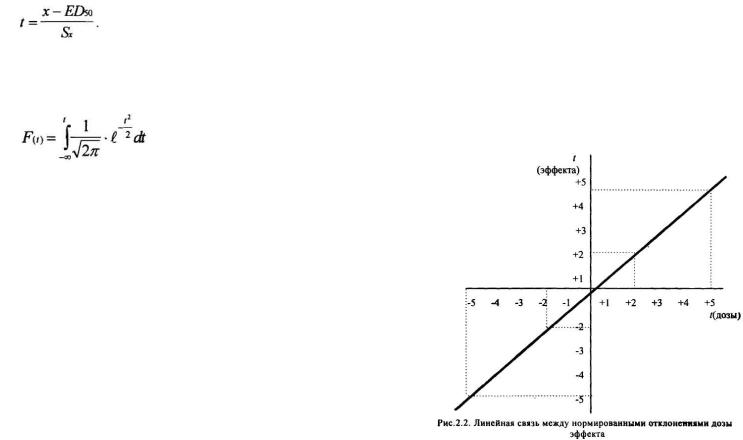
Уравнение (2.12) является уравнением первой степени и имеет графическое выражение в виде прямой линии. Предполагается, что любому значению t, выраженному через интегральную функцию нормального распределения,
(2.13)
соответствует значение вероятности эффекта на оси ординат, выраженное через ту же функцию (см. рис. 2.2). Например, если значение х из формулы (2.12) окажется равным среднеэффективной дозе, то нормированное отклонение t будет равно нулю. Такое же значение должна принять и величина эффекта на оси ординат, что соответствует значению интегральной функции нормального распределения равному 0.5 или 50%. И наоборот, если частота появления эффекта равна 83,3%, то это должно соответствовать нормированному отклонению дозы на оси ординат +1 и т.д. Указанные предположения и положены в основу построения функции эффективности при помощи пробит-анализа. Из этого следует фундаментальное положение о том, что в пробит-анализе в основе вычисления категорий эффективных доз лежит первоначальное построение по исходным данным функции эффективности, имеющей нормальное распределение.
Из рис. 2.2 видно, что нормированные отклонения могут принимать как положительные, так и отрицательные значения. Это вызывало неко-
торые неудобства, и, в ряде случаев, не обеспечивало визуальную линейную зависимость «доза-эффект». Для устранения этих явлений Блисс (Bliss C.I., 1938) предложил сместить значения нормированных отклонений по оси ординат в сторону положительных величин на 5 единиц (см. рис. 2.3). Именно это значение было выбрано, исходя из предположения о том, что вероятность появления нормированного отклонения меньшего -5 при условии нормального распределения функции эффективности не превысит 0.0001%. В регрессионном анализе данный прием называется смещением по оси, а величина смещения в этом случае не имеет значения. Поэтому вместо значения 5 можно было бы с тем же
успехом использовать любое другое значение. Величина, получаемая в результате смещения нормированных отклонений по оси ординат, получила название «пробит» от английского словосочетания «probability unit», т.е. «вероятностная единица».
Значения пробитов у определяют по формуле:
y = t + 5. (2.14)
Например, если частота эффекта (1/6) равна 16.7%, то из формулы (2.13), находим, что значение t = – 0.97. Из формулы (2.14) находим соответствующее значение пробита у=4.03. Для эффекта (5/6) значения показателей соответственно составят t=0.97, у=5.97 и т.д. Быстрый перевод процентов в пробиты можно осуществлять при помощи табл. 3 приложения.
