двумерные решения, которые применимы к преобразователям конечной ширины в одном направлении и бесконечным в другом. Физически эти решения отличаются тем, что эффекты дифракции описываются не jinc- функцией, а так называемой sinc-функцией, которая равна отношению

sinπx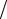πx . Кроме того, амплитуда поля убывает тогда с расстоянием как r−12 ,

поскольку плотность потока энергии в цилиндрически расходящемся пучке в силу закона сохранения полного потока энергии должна убывать как r−1 . Поэтому на одном и том же расстоянии от пре образователя дифракционные потери в цилиндрическом пучке меньше, чем в сферическом. На практике дифракционные потери прямоугольного преобразователя конечной длины h в направлении, перпендикулярном к h , будут приближаться к закону изменения r−12 в дальней зоне r >> h2 λ. Если l представляет собой больший из размеров

преобразователя, то при r >> l2 λ расходимость акустических волн снова будет сферической.

2.4 Поле сферического фокусирующего преобразователя

Пучок волн, излучаемых поршневым преобразователем, вследствие дифракции расходится в радиальном направлении. Поэтому на некотором расстоянии от преобразователя плотность потока энергии может быть очень низкой, тогда как диаметр пучка будет слишком большим для получения хорошего поперечного разрешения при зондировании какого-либо объекта. Поэтому часто используется фокусированный акустический пучок (как в оптике) с тем, чтобы получить хорошее поперечное разрешение и высокую интенсивность в акустическом пучке в интересующей точке.

Для фокусировки акустического пучка, как и в оптике, можно использовать линзы. Но в настоящее время проще оказывается фокусировать акустический пучок посредством преобразователя со сферической поверхностью, либо с помощью антенных решеток с электронным фокусированием. Обычно пучок удается сфокусировать в пятно с размером, меньшим диаметра преобразователя, так что интенсивность в фокальной области пучка может значительно превышать интенсивность на активной поверхности самого преобразователя.

Рассмотрим ультразвуковой преобразователь с диаметром активной поверхности W = 2a , формирующий сходящийся фокусированный волновой фронт с радиусом кривизны R0 . Формула (2.2) для акустического потенциала

преобразователя в абсолютно жестком экране является строго точной только в случае плоского поршневого преобразователя в плоском экране. Чтобы сразу избежать этой трудности, ограничимся рассмотрением плоской фазированной антенной решетки, для которой выражение (2.2) является строгим. Фокусирование поля при помощи фазированной решетки достигается путем электронного формирования различных временных задержек для сигналов возбуждения, подаваемых на различные элементы решетки.

В частности, для сферического фокусирования волн с геометрическим

фокусом в точке z = R0 сигнал возбуждения для элементов решетки с

радиальной координатой r′ подается с задержкой по времени τ ≈(a2 −r′2 )2R0c0

относительно краевых элементов с координатой a . Это означает, что к моменту начала работы центрального элемента решетки волны от элементов с ненулевой

сферическому. В результате эффективная акустическая длина хода для волн, излучаемых элементом с координатой r′, описывается теперь выражением

R = r2 + r′2 − 2rr′ sinθ cos(ψ′−ψ) − r′2 2R0 .

Из вида этого выражения следует, что для описания эффектов фокусирования необходимо использовать параксиальное приближение, или приближение Френеля, в котором при рассмотрении свойств пучка, излучаемого преобразователем, принимается, что a << z и, кроме того, в фазовых членах (в отличие от амплитудных) удерживаются квадратичные по малым величинам члены разложений. В параксиальном приближении имеем

слагаемых правой части, так как это величины второго порядка малости по r z , которые в итоге внесли бы вклад только в члены четвертого порядка по r

и r′. Следовательно, в параксиальном приближении предполагается малость не только величины r′, но и радиальной координаты точек наблюдения r , что

поясняет название этого приближения (параксиальный – близкий к оси). Из выражения (2.17) видно, что при z = R0 члены второго порядка по r′ взаимно

уничтожаются благодаря сферическому искривлению волнового фронта. Пренебрегая, как и ранее, изменением амплитуды волн с расстоянием, из (2.2) при подстановке в него (2.17) получаем

Интегрируя по угловой переменной, приходим к общему выражению вида

Рассмотрим теперь форму потенциала в плоскости z = R0 , которую в

приближении геометрической акустики следует считать фокальной плоскостью. На самом деле дифракционные эффекты приводят к смещению точки максимума интенсивности пучка на его оси ближе к поверхности фокусирующего ультразвукового преобразователя. В результате этого действительный фокус всегда находится в плоскости с координатой z < R0 . В

геометрической же фокальной плоскости потенциал на оси равен

eikR0

ϕ(0, R0 ) = v0a2 2R0 .

Отсюда находим амплитуду колебательной скорости и акустического давления

Тогда несложно вычислить интенсивность излучения в точке геометрического фокуса

последнее условие означает, что эффект от фокусирования волн наступает в этом случае в той области распространения пучка, где еще нет его большого дифракционного уширения, приводящего к сферической расходимости волн. Отношение γ = lF R0 называют степенью фокусирования волн, причем

фокусирующий преобразователь будет нормально работать только при достаточно большой степени фокусирования γ >1.

Как и ранее, исследуем сперва изменение акустического потенциала и, следовательно, давления и смещения вдоль оси рассмотренной фокусирующей системы. Точно так же, как и в случае плоского поршневого преобразователя, поле вдоль оси фокусирующего преобразователя изменяются очень быстро. В

пределе при R0 << a2 λ или S0 <<1 (т.е. глубоко в зоне Френеля) можно использовать эти результаты для определения глубины резкости dz (3дБ) как

расстояния между точками, где поля на оси меньше на 3дБ, чем в точке действительного фокуса. Для этого вернемся к формуле (2.19) и положим в ней r = 0 . Тогда это выражение может быть непосредственно проинтегрировано с

результатом

ϕ(0, z) =ϕ(0, R0 )F(z)eik ( z−R0 )e(i2S0 )( R0 z−1) ,

где

Из выражения (2.21) следует, что расстояние между точками, где поля на оси меньше на 3дБ, чем в фокусе можно найти, определив условия, при

которых функция F(z) становится равной 1/ 2 . Таким способом можно

определить величину глубины резкости, которая прямо связана со степенью фокусирования системы. Если имеется достаточно сильное фокусирование, то

Это выражение весьма удобно для оценки интенсивности пучка вдоль оси

Изменение интенсивности пучка в фокальной плоскости является точно таким же по форме, как и в зоне Фраунгофера плоского поршневого преобразователя. Однако теперь интенсивность пучка можно выбрать по желанию, и она может намного превышать интенсивность на самом излучателе, что меняет масштабы изменения поля как в осевом, так и в радиальном направлениях.

3. ОСНОВЫ НЕЛИНЕЙНОЙ АКУСТИКИ

3.1Кумулятивные эффекты нелинейного взаимодействия

Вобщем случае нелинейные механизмы взаимодействия ультразвука с биологическими средами включают в себя не только кавитацию и ассоциированные с ней процессы. Они определяют также: 1) изменение формы ультразвуковых волн с расстоянием, 2) генерацию гармоник основной частоты излучения и формирование пилообразных волн, 3) возрастание поглощения ультразвука в тканях из-за передачи энергии гармоникам и их более эффективным поглощением. При изучении этих механизмов различают кумулятивные и локальные нелинейные эффекты взаимодействия, поскольку в зависимости от конкретных биомедицинских приложений и те и другие могут играть важную роль и приводить к различным биоэффектам.

Под кумулятивными понимают эффекты, связанные с накоплением результата действия нелинейности биологической среды. В частности, кумулятивным (накапливающимся) является искажение формы синусоидальной волны при ее распространении в биологической среде с однородным распределением нелинейных свойств. Отклонения же от некоторого среднего уровня нелинейности приведут к локальным эффектам взаимодействия волн с неоднородностью по параметру нелинейности. Тепловыделение при поглощении волн по смыслу кумулятивно, но при сильном фокусировании пучка волн возрастание их поглощения тканью в фокальной области из-за усиленной генерации гармоник будет иметь локальный характер.

Наиболее фундаментальным для понимания всех кумулятивных эффектов взаимодействия с нелинейными средами, к которым относятся и биологические ткани, является полученное Риманом еще в 1860г. нелинейное решение уравнений Эйлера. Из него следует, что волновые возмущения – области сжатия и разрежения, движутся с разной фазовой скоростью:

для конденсированных сред эмпирическими константами, описывают квадратичную нелинейность в функции зависимости давления от плотности:

нелинейности ε обусловлена, как правило, не конвективным движением частиц среды, а отношением B2A , характеризующим ее нелинейные свойства.

В плоской гармонической волне акустическое давление достигает своего амплитудного значения в те же моменты времени, что и колебательная скорость. Это вытекает из определения (1.13)-(1.14) этих величин через акустический потенциал. Выражение (3.1) показывает, что области сжатия, где vx > 0, движутся со скоростями большими, чем области разрежения (vx < 0 ),

скорость которых, кроме того, меньше c0 . В результате с увеличением

расстояния синусоидальные волны деформируются – области сжатия догоняют области разрежения, придавая волне пилообразный профиль. Характерное расстояние, на котором в плоской гармонической волне образуется разрыв давления, дается выражением:

где M = v0 c0 - акустическое число Маха, v0 и PA - амплитуда колебательной

скорости и акустического давления.

Пройденное волной расстояние принято выражать в безразмерном виде

Вблизи излучателя, где σ < 0,1, распространение волн с хорошей точностью

можно считать линейным. При σ =1 начинается формирование разрыва акустического давления в точке перехода от области сжатия к области разрежения, который представляет собой фронт ударной волны. Наконец, при σ = 3 формируется нелинейная пилообразная волна, показанная на рис.3.1. Важно, что для частот и интенсивностей излучения диагностического ультразвука диапазон расстояний σ зависит от режима визуализации и расположен в интервале значений от долей единицы до 3. Это означает, что практически рассматриваемым кумулятивным эффектом нелинейного взаимодействия никогда нельзя пренебречь не только для терапевтических, но и диагностических приложений.

Особенностью решения для интервала значений 1 <σ < 3 , показанного на рис.3.1 является то, что уже при относительно небольшом увеличении любого из параметров, фигурирующих в выражении (3.4), например ε , форма волны, соотношение гармонических составляющих и величина разрывов давления на

Рис.3.1. Изменение профиля синусоидального возмущения в нелинейной среде при характерных для медицинских приложений значениях σ .

ударных волновых фронтах могут изменяться весьма значительно. Увеличение в 2-3 раза амплитуды акустического давления излучаемых пучков волн является совершенно естественным для разных режимов визуализации и может приводить к переходу от формирования разрывов давления к установившейся ударной пилообразной волне с высоким уровнем гармоник.

Для плоской волны при σ <<1 амплитуда n -й гармоники пропорциональна PAn . С увеличением σ относительный уровень амплитуды гармоник возрастает

и при σ = 3, когда волна становится пилообразной, их амплитуда обратно пропорциональна номеру гармоники. В табл.3.1 показаны уровни амплитуды гармонических составляющих в плоской волне при двух значениях безразмерного расстояния σ .

Таблица 3.1 Приближенные значения величины амплитуды гармоник Pn относительно

амплитуды акустического давления PA фундаментальной частоты

Приведенные в табл.3.1 данные лишь качественно описывают ситуацию для ультразвуковых полей, используемых в терапии и диагностике, поскольку не учитывают релаксационные процессы в биологических тканях, дифракцию волн, их фокусирование и импульсный характер излучения, что является обычным для диагностических устройств. Из-за дифракции волн в ближней зоне ультразвуковое поле сильно изменяется от точки к точке, при этом минимумы в распределении поля основной частоты оказываются заполненными гармониками. Поэтому отношение гармонических амплитуд для каждой точки среды отнюдь не следует простым соотношениям табл.3.1. Кроме того, появляются сдвиги по фазам между основной частотой и гармониками, что проявляется в асимметрии величины давления в фазах сжатия и разрежения (рис.3.2а). Искажения профиля волны в центральной части импульса, где высока амплитуда колебаний, проявляются раньше и выражены сильнее. Иной тип возможных искажений профиля пилообразной волны, показанный на рис.3.2б, связан с влиянием дисперсии скорости звука среды. В отсутствие диссипации энергии дисперсия привела бы к распаду начального возмущения на ряд слабо взаимодействующих солитонов. В среде с диссипацией этот процесс сглажен и приводит к слабым пульсациям давления в фазе сжатия, которые можно заметить и на рис.3.2а.

Даже слабое фокусирование волн, характерное для диагностических приложений, существенно изменяет параметры нелинейного распространения. В префокальной области безразмерное расстояние (3.4) растет нелинейно из-за увеличивающейся с расстоянием амплитуды волн. Поэтому по сравнению с