1.1 Примеры решения задач и контрольное задание по разделу кинематика материальной точки Методические указания

1. Прямая задача кинематики: по известному закону движения определить характеристики движения (скорость, ускорение, траекторию). Задача решается путем дифференцирования уравнения, выражающего закон движения, а также с помощью формул связи одних характеристик движение с другими.

2. Обратная задача: по известным характеристикам движения найти закон изменений координат и радиус-вектора во времени. Задача решается интегрированием уравнения движения.

Для нахождения траектории движения, т.е. для установления связи между координатами у = f(х), следует исключить время из системы уравнений, выражающих законы движения вдоль координатных осей.

Пример 1.

Уравнение движения материальной точки вдоль оси x имеет вид х = A+Bt+Ct², где A = 3 м, B = 2 м/с, C = - 0,5 м/c². Найти координату х, скорость V, ускорение a точки в момент времени t = 4 с.

Решение

Координату x найдем, подставив в уравнение движения числовые значения коэффициентов A, B, C и времени t:

x = (3+2 4+(- 0,5) 4²) = 3 м.

Мгновенная скорость есть первая производная от координаты по времени:

V = dx/dt = B+2Ct.

В момент времени t = 4 с имеем V = 2+2 (-0,5) 4 = - 2м/с.

Ускорение точки найдем, взяв первую производную от скорости по времени:

a = dV/dt = 2C.

В момент времени t = 4 с получаем a = 2(-0,5) = -1 м/с².

Пример 2.

Пуля выпущена с начальной скоростью V_о= 200 м/с под углом α = 60° к горизонту. Определить максимальную высоту H_max подъема, дальность S полета и радиус R кривизны траектории пули в её наивысшей точке. Сопротивлением воздуха пренебречь.

Решение

Выберем систему координат так, как показано на рисунке. В любой точке траектории на тело будет действовать только сила тяжести, направленная вертикально вниз. Следовательно, вдоль оси x движение будет равномерным, а вдоль оси y - равноускоренным. Так как в начальный момент в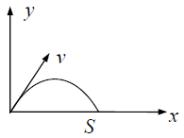 ремени координаты тела равны нулю, то уравнения движения тела могут быть записаны следующим образом:

x = V_0x t , y = V_0y t - gt²/2 ,

где обозначено V_x = V₀cosα и V_y= V₀sinα - проекции скорости в момент времени t на оси x и y. Когда тело достигнет максимальной высоты, то V_y= 0. Следовательно, V₀sinα = =gt_max, откуда находим время t_max, за которое пуля достигнет верхней точки: t_max= V₀sinα/g. В верхней точке y = H_max. Подставляя в уравнение движения вдоль оси y найденное значение t_max, получаем: .

В точке падения пули на землю у = 0. Подставляя в уравнение движения вдоль оси у значение y = 0 и сокращая на t, получаем: ,

где t_s – полное время движения пули.

Отсюда находим .

Подставляя найденное значение в уравнение движения вдоль x, получаем: .

Для определения радиуса кривизны траектории в наивысшей точке заметим, что в каждой точке траектории полное ускорение равно ускорению силы тяжести. В верхней точке траектории оно равно центростремительному ускорению, то есть: ,

откуда следует, что .

Подставляя численные значения в выражения для R, S и H_max, получим R = 1,02 км, S = 3,53 км, H_max= 1,53 км.

Пример 3.

Колесо вращается с постоянным угловым ускорением ε = 2 рад/с². Через t = 0,5 с после начала движения полное ускорение колеса стало равно a = 13,6 см/с². Найти радиус колеса R.

Решение

Так как угловое ускорение постоянно, а начальная угловая скорость равна нулю, угловую скорость ω в зависимости от времени можно вычислить следующим образом: ω = εt. Линейная скорость точек на краю колеса будет равна: V = ωR = εRt.

Полное ускорение точек на ободе колеса будет равно: .

Откуда получаем: .

Подставляя численные значения, находим: R = 0,061 м.