
І рівень складності
Альтернативні тести
Оберіть номер правильної відповіді
Середня арифметична зважена обчислюється за формулою:
а)
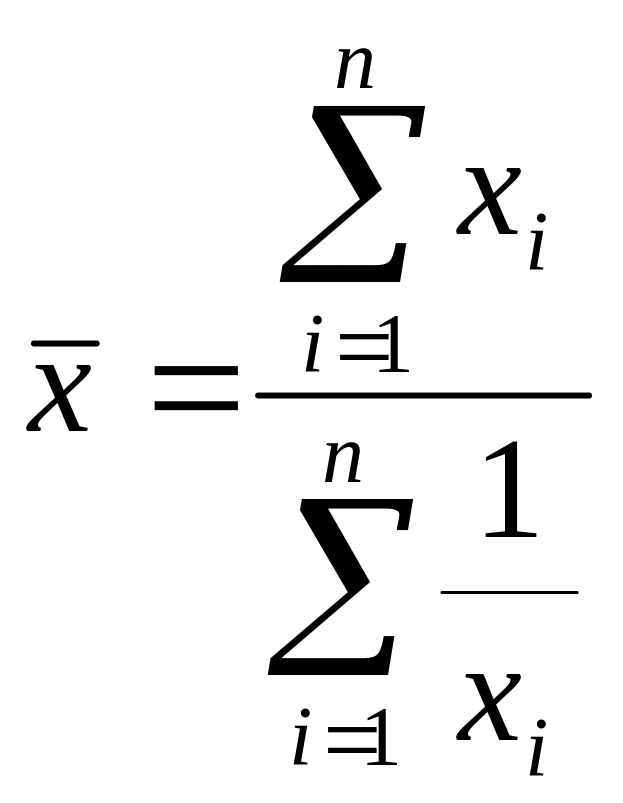 ;
б)
;
б)
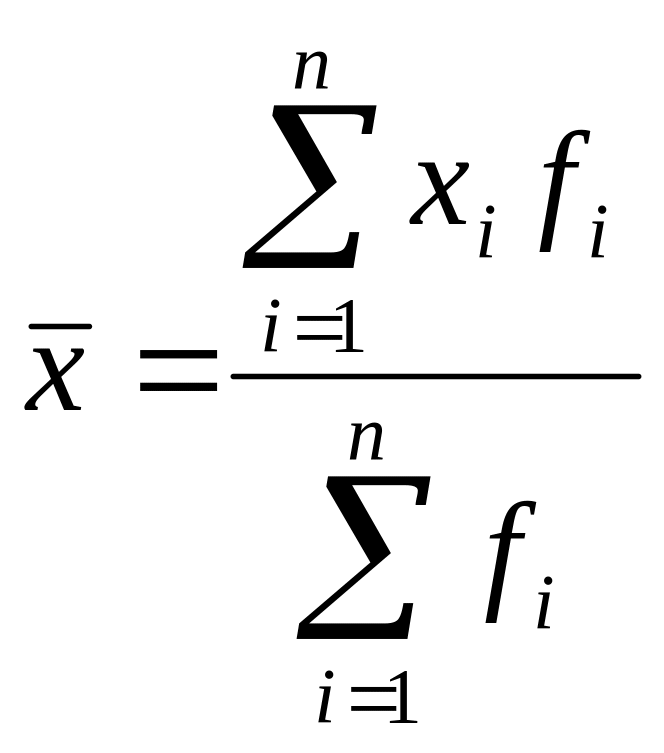 ;
в)
;
в)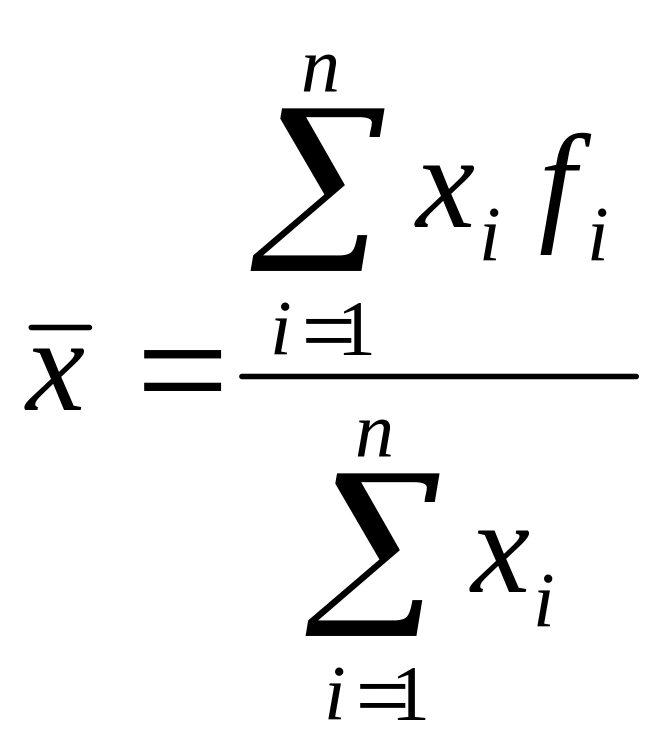 ;
г)
;
г)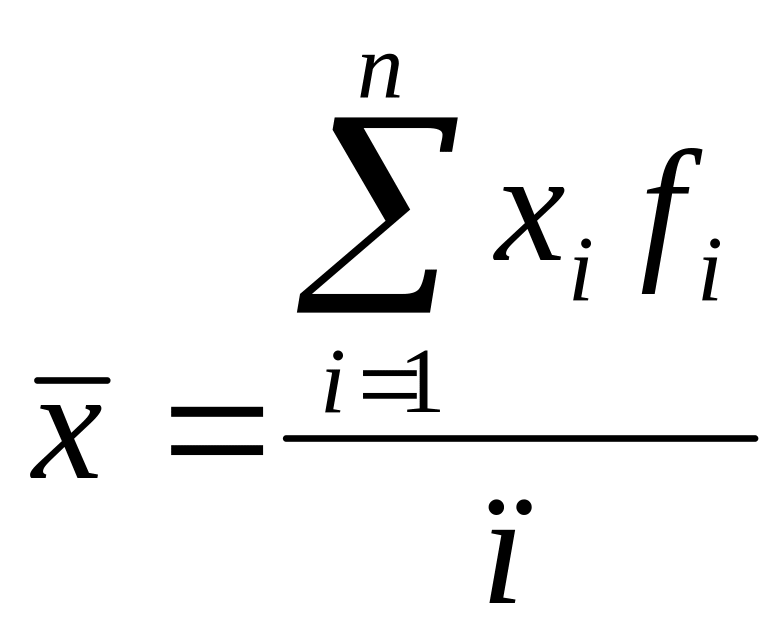 .
.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Якщо вихідні дані представлені у вигляді інтервального ряду розподілу, середину інтервалу обчислюють як:
різницю між максимальним і мінімальними значення ознаки;
різницю між верхньою та нижньою межею інтервалу;
суму між верхньою та нижньою межею інтервалу;
півсуму верхньої та нижньої межі інтервалу.
Відповіді: 1) а; 2) б; 3) в; 4) г
Середню гармонійну просту обчислюємо за формулою:
а)
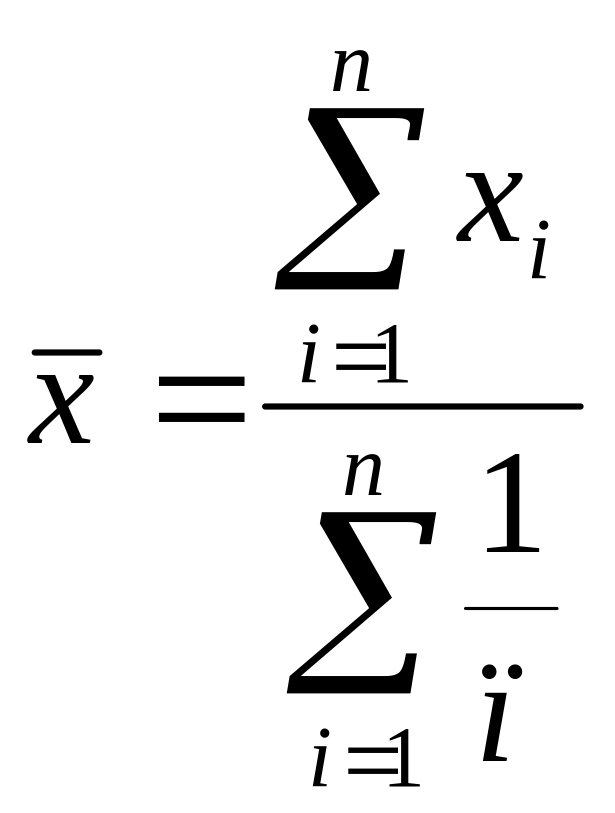 ;
б)
;
б)
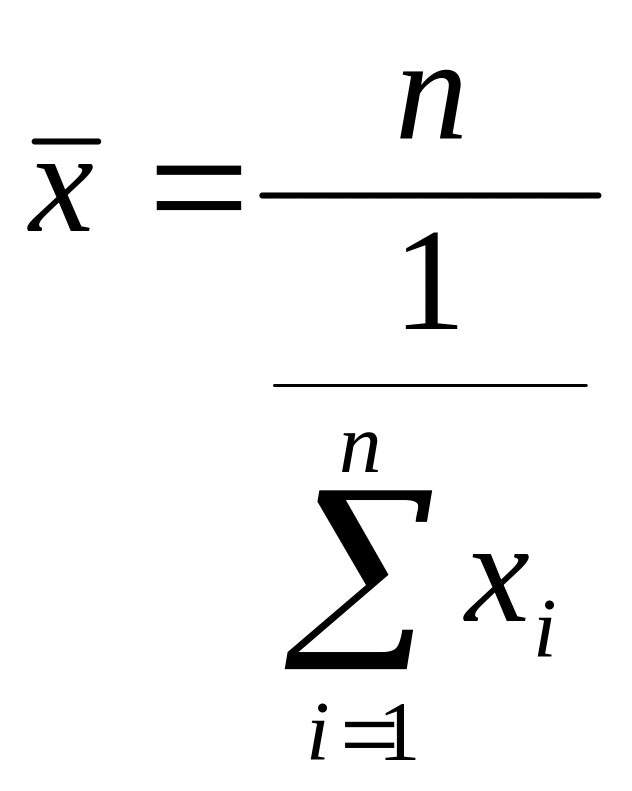 ;
в)
;
в)
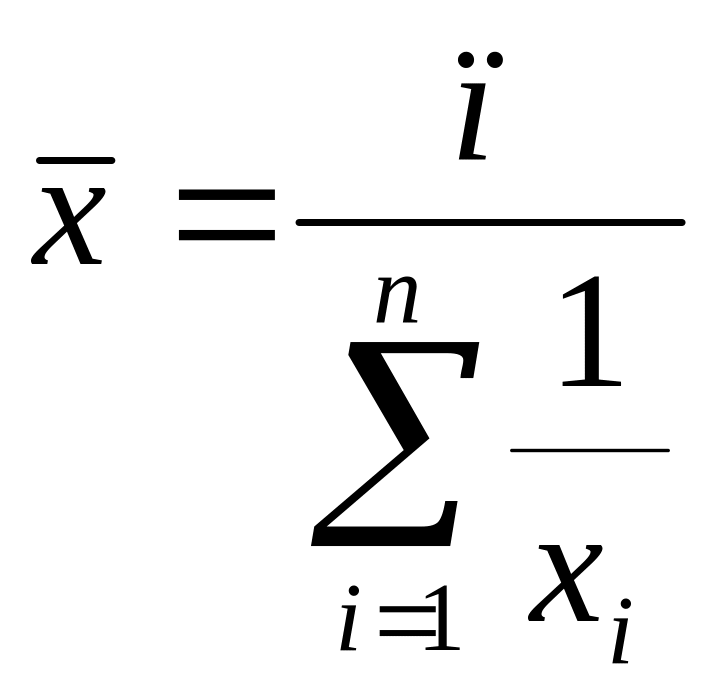 ;
г)
;
г)
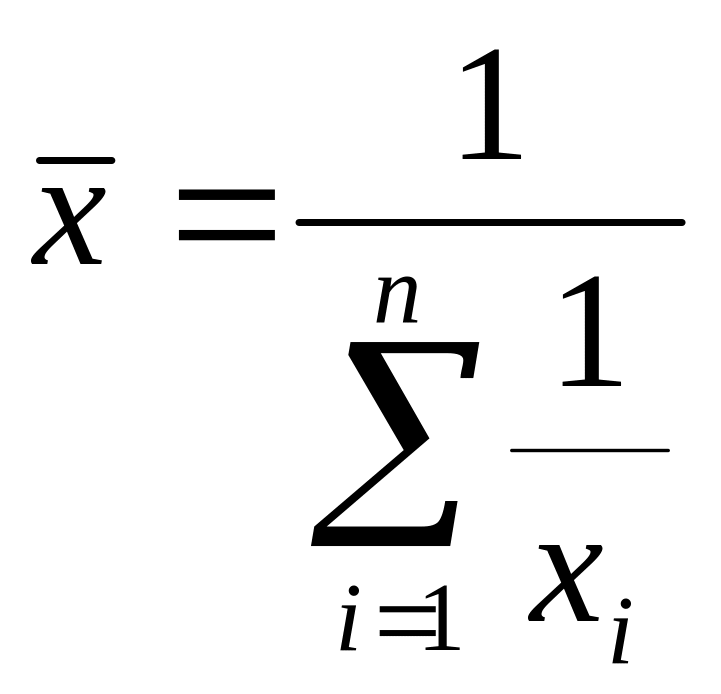 .
.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Середня гармонійна – це:
величина, що завжди знаходиться в середині варіаційного ряду;
величина ознаки, яка найчастіше зустрічається у сукупності;
величина, обернена арифметичній з обернених (за економічним змістом) значень ознаки;
величина, що ділить ряд розподілу на дві рівні частини.
Відповіді: 1) а; 2) б; 3) в; 4) г.
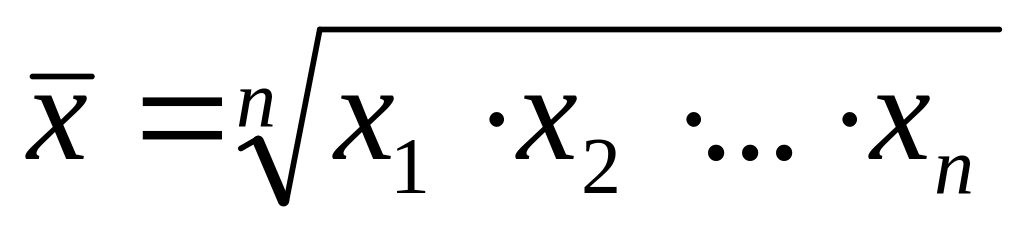 – це
формула середньої:
– це
формула середньої:
гармонійної;
квадратичної;
арифметичної;
геометричної.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Для визначення середнього діаметру циліндричних тіл використовують середню:
а) арифметичну;
б) геометричну;
в) квадратичну;
г) гармонійну.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Згідно з властивостями середньої має місце таке твердження:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Якщо всі варіанти дискретного ряду розподілу зменшити у 3 рази, а частоти залишити без змін, то середнє значення ознаки:
збільшиться на 3;
зменшиться у 3рази;
зменшиться у 9 разів;
залишиться незмінним.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Якщо всі частоти дискретного ряду розподілу зменшити у 4 рази, а індивідуальні значення ознаки залишити без змін, то середнє значення ознаки:
Збільшиться на 4;
зменшиться у 4 рази;
зменшиться у 16 разів;
залишиться незмінним.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Модою дискретного ряду розподілу вважається:
найбільше значення частоти або частки;
найбільше значення ознаки;
значення ознаки, що має найбільшу частоту або частку;
різниця між найбільшим і найменшим значеннями ознаки.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Медіаною дискретного ряду розподілу вважається:
Найбільше значення ознаки;
значення ознаки, кумулятивна частота якого дорівнює половині обсягу сукупності або її перевищує;
найбільше значення кумулятивної частоти;
найбільше значення частоти (частки).
Відповіді: 1) а; 2) б; 3) в; 4) г.
Варіанти, які поділяють сукупність на чотири рівні частини, називають:
децилями;
квартилями;
квінтелями;
перцентелями.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Моду в інтервальному ряді розподілу визначають за формулою:
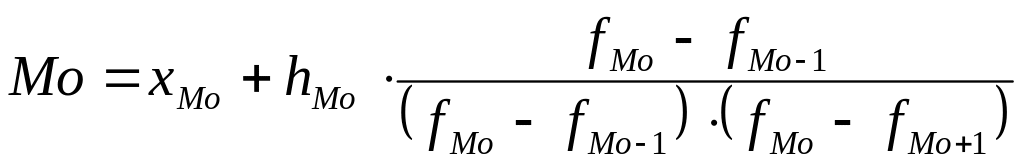 ;
;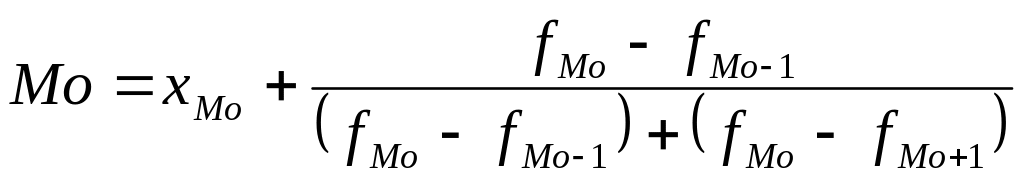 ;
;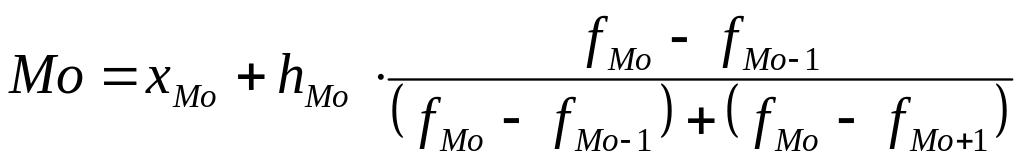 ;
;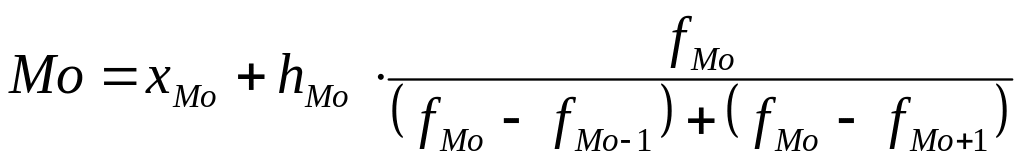 .
.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Згідно з правилом мажорантності, середня арифметична (
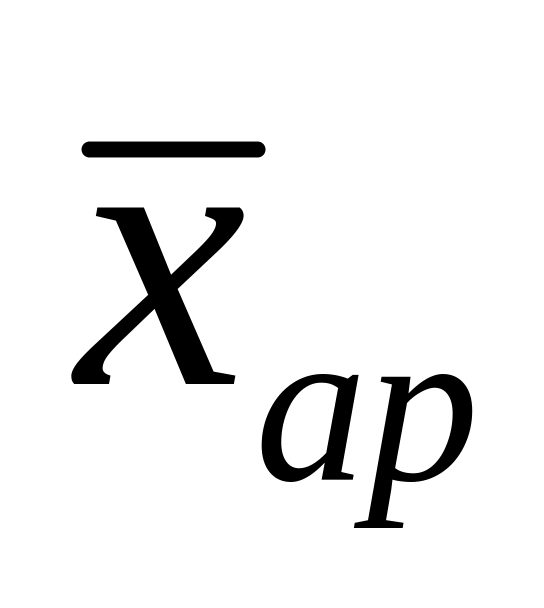 ),
середня гармонійна (
),
середня гармонійна ( ),
середня геометрична (
),
середня геометрична (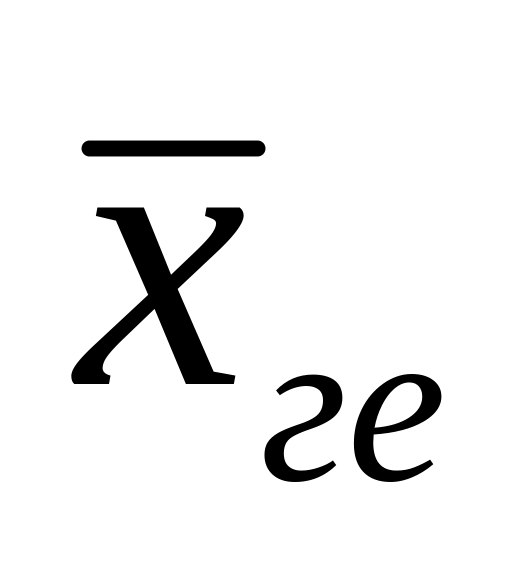 )
і середня квадратична (
)
і середня квадратична (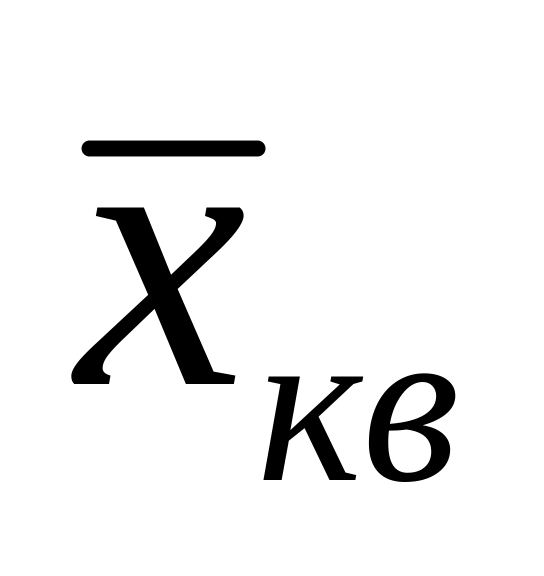 )
перебувають у такому співвідношенні:
)
перебувають у такому співвідношенні:
а)
![]() <
<
![]() <
<
![]() <
<
![]() ;
;
б)
![]() <
<
![]() <
<
![]() <
;
<
;
в) < < < ;
г) < < < .
Відповіді: 1) а; 2) б; 3) в; 4) г.
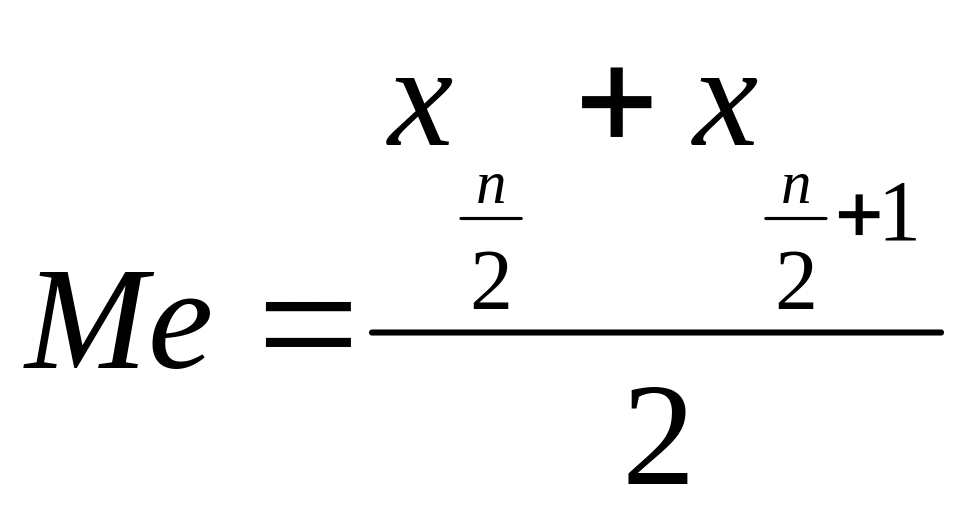 – це
формула, за допомогою якої обчислюють
медіану для:
– це
формула, за допомогою якої обчислюють
медіану для:
згрупованих даних;
незгрупованих даних;
парної кількості одиниць сукупності;
непарної кількості одиниць сукупності.
Відповіді: 1) а, в; 2) б, в; 3) а, г; 4) б, г.
За даними про стаж роботи кожного працівника і кількість працівників підприємства, середній стаж роботи працівників слід визначати за допомогою середньої:
а) арифметичної простої;
б) арифметичної зваженої;
в) гармонійної простої;
г) гармонійної зваженої.
Відповіді: 1) а; 2) б; 3) в; 4) г.
За даними про собівартість одиниці продукції та кількість реалізованої продукції підприємства, середню собівартість слід визначати за допомогою середньої:
а) арифметичної простої;
б) арифметичної зваженої;
в) гармонійної простої;
г) гармонійної зваженої.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Рівень безробіття змінювався відносно попереднього року: у 2008 р. – у 1,3 рази; 2009 р. – у 2 рази; 2010 р. – у 1,5 рази. Середньорічний рівень безробіття можна розрахувати за формулою середньої:
а) арифметичної;
б) геометричної;
в) квадратичної;
г) гармонійної.
Відповіді: 1) а; 2) б; 3) в; 4) г.
За даними про урожайність та валовий збір пшениці, середню урожайність слід визначати за допомогою середньої:
а) арифметичної простої;
б) арифметичної зваженої;
в) гармонійної простої;
г) гармонійної зваженої.
Відповіді: 1) а; 2) б; 3) в; 4) г.
Для варіаційного ряду розподілу справедливі такі твердження:
а) мода – це варіант із найбільшою частотою;
б) другий квартиль дорівнює медіані;
в) п’ятий дециль дорівнює медіані;
г) шостий дециль дорівнює моді.
Відповіді: 1) а; 2) а, в; 3) а, г; 4) а, б, в.
Другий дециль ряду розподілу працівників підприємства за рівнем заробітної плати дорівнює 1,5 тис. грн. Це означає, що:
а) доходи 80% працівників перевищують або рівні 1,5 тис. грн;
б) доходи 20% працівників перевищують або рівні 1,5 тис. грн;
в) доходи 80% працівників не перевищують 1,5 тис. грн;
г) доходи 20% працівників не перевищують 1,5 тис. грн.
Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г.
Третій квартиль ряду розподілу домогосподарств за доходами дорівнює 870 грн. Це означає, що:
а) доходи 75% домогосподарств перевищують або рівні 870 грн;
б) доходи 25% домогосподарств перевищують або рівні 870 грн;
в) доходи 25% домогосподарств не перевищують 870 грн;
г) доходи 75% домогосподарств не перевищують 870 грн.
Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г.
Якщо середній нормований бал більший за нуль, то явище характеризується узагальненою:
а) позитивною оцінкою
б) негативною оцінкою.
Чи залежить значення нормованого середнього балу від розмірностей порядкової шкали?
в) так;
г) ні.
Відповіді: 1) а, в; 2) а, г; 3) б, в; 4) б, г.
