1.Расчет на усталостную прочность

1.2. Расчет детали на усталостную прочность

В данном разделе необходимо определить фактический коэффициент запаса прочности гидроцилиндра, а также проверить условие прочности.

Вероятный вид разрушения – усталостная поломка.

Критерий расчета – усталостная прочность.

Коэффициент запаса прочности может быть определен по формуле

; (1.1)

где S – фактический коэффициент запаса; - предельное напряжение, Н/мм ;

- максимальное фактическое напряжение, Н/мм .

Максимальное фактическое напряжение можно определить по формуле

; (1.2)

где - усилие стойки при растяжении (рис. 1.1), Н; - минимальная площадь, мм .

Минимальную площадь опасного сечения штока найдем по формуле

; (1.3)

где d – диаметр опасного сечения, мм.

Подставив числа в формулу (1.3), найдем минимальную площадь опасного сечения штока

мм

Подставляя численное значение в выражение (1.2), получаем

Н/мм

Найдем по формуле

; (1.4)

Подставляя численные значения в выражение (1.4), получаем

Н/мм

_{Построим график изменения напряжения в штоке (рис. 1.2)}

_{Цикл изменения напряжения}

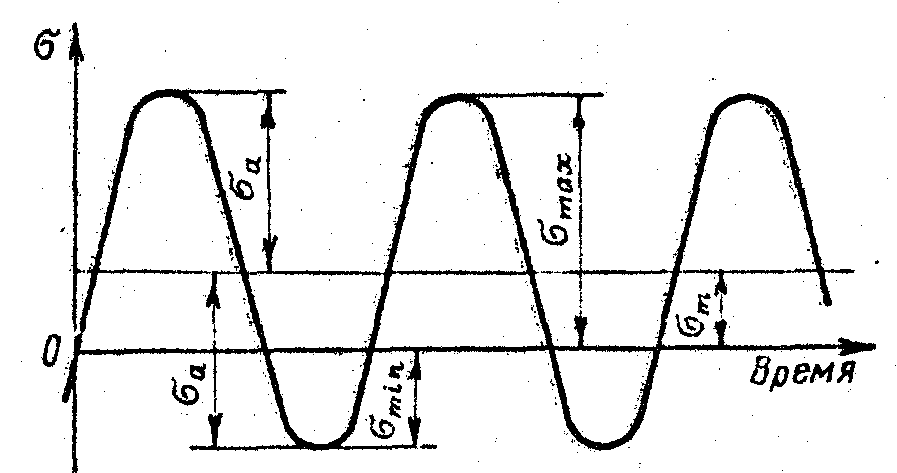
_{Из рассмотрения рис. 1.2 следует, что в качестве предельных напряжений следует выбрать предел усталости при произвольном цикле для детали при ограниченном числе циклов , так как опыт эксплуатации подобных механизмов показывает, что причиной их разрушения является усталостная поломка. определяется по формуле [1, с.33].}

; (1.5)

где – предел усталости при произвольном цикле для детали и ограниченном числе циклов, Н/мм²; – предел усталости при симметричном цикле и ограниченном числе циклов для детали, Н/мм²; R – коэффициент асимметрии цикла; – коэффициент чувствительности детали к асимметрии цикла.

Определим коэффициент асимметрии цикла

; (1.6)

Подставляя численные значения в выражение (1.6), получим

Определим предел усталости при симметричном цикле и ограниченном числе циклов по формуле [1, с.30]

; (1.7)

где К₀ – коэффициент, учитывающий количество циклов; – предел длительной выносливости для детали при симметричном цикле, Н/мм², который определяется по формуле

; (1.8)

где К – коэффициент снижения предела выносливости.

Учитывая материал штока – Сталь 45 и зная, что Н/мм², Н/мм² [1, с.74], найдем предел выносливости гладкого стандартного образца по формуле [1, с.77]

Н/мм² (1.9)

Определим значение коэффициента снижения предела выносливости К, который учитывает влияние различных факторов, по формуле [1, с.21]

; (1.10)

где – коэффициент концентрации напряжений; – коэффициент,

учитывающий масштабный фактор; – коэффициент, учитывающий шероховатость поверхности штока; – коэффициент, учитывающий упрочняющие технологии; – коэффициент, учитывающий анизотропию материалов.

Так как в данном случае деталью является шток, следовательно, заготовка представляет собой прокат, то есть [1, с.29]. Считая, что дополнительное упрочнение не производилось, первоначально принимаем .

Определим по формуле [1, с.22]

; (1.11)

где q – коэффициент чувствительности металла к концентрации напряжений; – теоретический коэффициент концентрации напряжений.

Найдем по графику [1, с.78]. Учитывая, что и получаем .

При коэффициент чувствительности металла к концентрации напряжений [1, с.84].

Подставляя полученные значения в выражение (1.11), получаем

Коэффициент при d = 50 мм будет равен [1, c.85], а коэффициент при Н/мм и мкм будет равен [1, с.85].

Подставляя численные значения в формулу (1.10), получаем

Подставляя численные значения в формулу (1.8) и получаем

Н/мм

Определим по формуле [1, с.30]

; (1.12)

где - базовое число циклов напряжений, соответствующие точке перелома кривой усталости; N – число циклов; m – показатель степени кривой усталости.

принимаем равным циклов [1, с.30].

Считая, что , определяем по формуле [1, с.30]

; (1.13)

Подставляя численные значения в формулу (1.13), получим

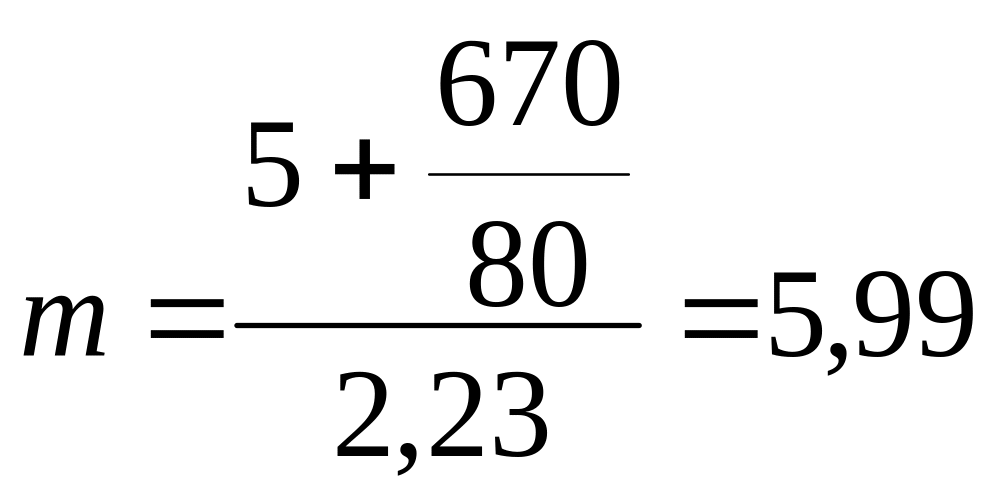
Подставляя значения в выражение (1.12)

Подставляем значения в выражение (1.7), получаем

Н/мм

Определим коэффициент чувствительности детали к асимметрии цикла по формуле [1, c.31].

; (1.14)

где - коэффициент чувствительности к асимметрии цикла, находящийся по эмпирической формуле [1, с.31]

; (1.15)

Подставляя значения в формулу (1.15), получим

Подставляя численные значения в формулу (1.14), получаем

Теперь мы располагаем всеми данными, необходимыми для расчета предела усталости в произвольном цикле для детали при ограниченном числе циклов .Подставляя численные значения в выражение (1.5), получаем

Н/мм

Так как Н/мм < Н/мм , Н/мм .

Вычисляем фактический коэффициент запаса прочности S по формуле (1.1), принимая , получаем

Проверим условие прочности для данного штока

; (1.16)

В данном случае, принимая во внимание то, что исходные данные и результаты расчета имеют пониженную точность, назначаем коэффициент запаса прочности [1, с.87].

Таким образом, видно, что, . То есть, при изготовления штока стали 40Х по указанным в техническом задании размерам, будет обеспечено отсутствие усталостной поломки при заданных нагрузках и ресурсе в двойных ходов без дополнительной обработки поверхности штока в опасном сечении.