Аналогия между электрическим полем постоянного тока и электростатическим полем
Электрическое поле постоянного тока в однородной проводящей среде аналогично электростатическому полю в однородном диэлектрике, если конфигурация рассматриваемых областей в обоих случаях одинакова и, кроме того, одинаковы граничные условия для потенциалов. Эта аналогия позволяет использовать известные решения электростатических задач для нахождения электрического поля постоянного тока и наоборот.
В качестве примера
применения указанной аналогии вычислим
сопротивление
между электродами, находящимися в
однородной проводящей среде. Пусть
потенциалы электродов равны
и
,
причем
.
Согласно закону Ома
, (7.7.7)
где — ток между электродами. Очевидно,
, (7.7.8)
где — замкнутая поверхность, охватывающая один из электродов. Подставляя ф-лу (7.7.8) в (7.7.7) и учитывая, что , получаем
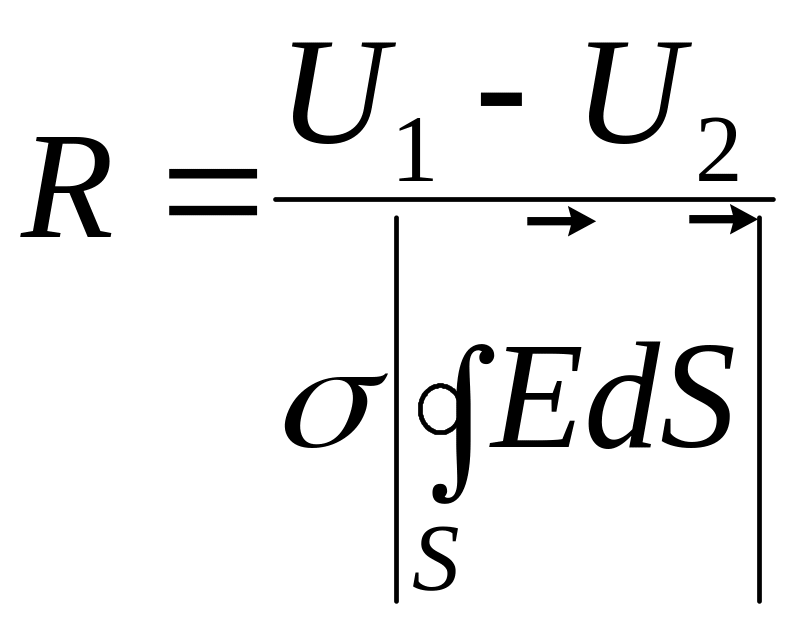. (7.7.9)
Для определения
величины
рассмотрим другую задачу.
Пусть такие же электроды находятся в однородном идеальном диэлектрике, характеризуемом диэлектрической проницаемостью . Поток вектора через поверхность при этом, согласно теореме Гаусса, равен
, (7.7.10)
где
— заряд электрода, находящегося внутри
поверхности
.
Если потенциалы
электродов в этом случае также равны
и
,
то на основе указанной аналогии можно
утверждать, что интеграл
в ф-лах (7.7.9) и (7.7.10) имеет одно и то же
значение. Так как из определения емкости
системы двух проводников следует, что
,
то
. (7.7.11)
Подставляя ф-лу (7.7.11) в (7.7.9), получаем
. (7.712)
Используем ф-лу (7.7.12) для определения сопротивления утечки изоляции коаксиального кабеля. Емкость на единицу длины коаксиального кабеля или, что то же самое, емкость на единицу длины цилиндрического конденсатора определяется ф-лой
.
Подставляя эту ф-лу в (7.7.12), получаем, что сопротивление утечки на единицу длины коаксиального кабеля
, (7.7.13)
где
—удельная
проводимость изоляции кабеля;
— радиус внутреннего провода кабеля,
а
— внутренний радиус оболочки кабеля.