Поле двухпроводной линии
Рассмотрим сначала
поле двух линейных противоположно
направленных токов
и
,
т.е. токов, протекающих по бесконечно
тонким прямолинейным нитям, расположенным
на расстоянии
друг от друга (рис. 3).
Рис. 3
Векторный потенциал имеет только составляющую, параллельную оси , и в силу принципа суперпозиции равен сумме потенциалов каждого из токов:
, (7.6.13)
где
.
Поверхности, на которых векторный потенциал (7.6.13) имеет постоянное значение, определяются из условия
. (7.6.15)
Такому же условию удовлетворяют эквипотенциальные поверхности системы двух параллельных противоположно заряженных нитей. Следовательно, поверхности равного векторного потенциала являются поверхностями круговых цилиндров, параллельных оси , местоположение осей и радиусы которых определяются ф-лами
и
,
а магнитные силовые линии образуют семейство окружностей, возникающих при пересечении этих цилиндрических поверхностей с плоскостями, перпендикулярными оси (рис. 4).
Рис. 4
Вычислим индуктивность
на единицу длины двухпроводной линии.
Для простоты ограничимся случаем тонких
проводов, когда расстояние между осями
проводов
велико по сравнению с их радиусом
.
Воспользуемся ф-лой
.
В рассматриваемом
случае
.
Поэтому магнитный поток, сцепленный с
двухпроводной линией, приходящийся на
единицу ее длины, практически равен
магнитному потоку, пронизывающему
прямоугольный контур
(рис. 5), расположенный в плоскости
,
проходящей через оси проводов. Стороны
и
,
параллельные оси
,
имеют единичную длину и лежат на
поверхности проводов (
на
и
на
соответственно).
Рис. 5
Используя соотношение
для
и учитывая
,
находим значение вектора
в плоскости
. (7.6.16)
Учитывая
,
вычислим магнитный поток, пронизывающий
контур
:
. (7.6.17)
Следовательно, индуктивность на единицу длины двухпроводной линии в случае определяется выражением
. (7.6.18)
Поле кругового контура с током
Вычислим поле линейного тока , образующего круговой виток радиуса (рис.6).
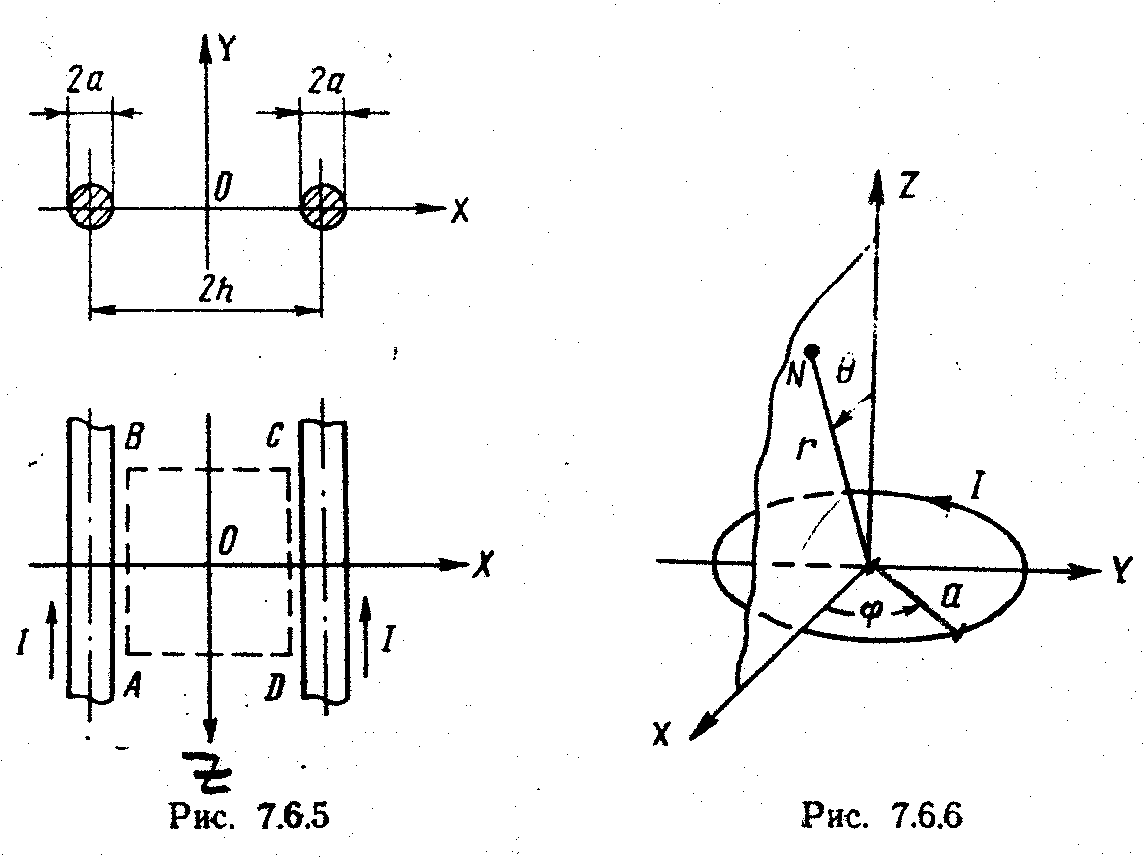
Рис. 6
Введем сферическую
систему координат
,
полярная ось которой совпадает с осью
симметрии, а начало координат — с центром
витка. Благодаря симметрии задачи начало
отсчета угла
можно выбрать произвольно. Будем
отсчитывать его от плоскости, проходящей
через полярную ось и точку наблюдения
,
в которой вычисляется поле.
Для определения
векторного потенциала воспользуемся
выражением
.
Проектируя вектор
на направления
,
соответствующие точке наблюдения
,
получаем
.
Следовательно,
, (7.6.19)
где
.
Переходя в интеграле
(7.6.19) к новой переменной интегрирования
и вводя обозначение
;
,
получаем
, (7.6.20)
где
— полные эллиптические интегралы первого и второго рода соответственно.
Эллиптические
интегралы не выражаются через элементарные
функции, однако они подробно изучены,
и имеются таблицы их значений в зависимости
от величины
,
называемой модулем
этих интегралов.
Для вычисления
вектора
воспользуемся соотношением
.
В сферической системе координат выражение
для
имеет вид:
.(7.6.21)
Так как векторный
потенциал
имеет только одну составляющую
,
не зависящую от угла
,
из ф-лы (7.6.21) следует, что напряженность
магнитного поля имеет две составляющие
и
,
связанные соотношениями:
; (7.6.22)
. (7.6.23)