
3°. Выражение скалярного произведения через компоненты сомножителей. Матрица Грама.
Пусть
в произвольном евклидовом пространстве
задан базис
.
Это позволяет
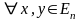 представить в виде
представить в виде
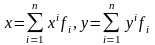 .
Вычислим скалярное произведение
:
.
Вычислим скалярное произведение
:
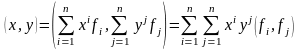 .
.
Отсюда
следует, что если базис
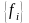 − ортонормированный, то есть
− ортонормированный, то есть
 ,
то
,
то
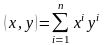 .
.
Теорема 5. В ортонормированном базисе скалярное произведение любых двух векторов равно сумме произведений соответствующих координат этих векторов.
Если
же базис { }
− произвольный, то произведения
}
− произвольный, то произведения
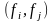 обозначим
обозначим
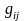 и введем в рассмотрение квадратную
матрицу
и введем в рассмотрение квадратную
матрицу
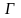 =
=
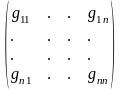 =
=
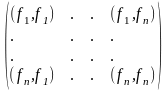 ,
,
называемую
матрицей Грамма базиса {
}.
В силу коммутативности скалярного
произведения
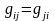 ,
т.е. матрица Грама симметрическая.
,
т.е. матрица Грама симметрическая.
Обозначим
 =
=
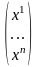 ,
,
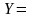
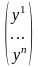 .
Тогда скалярное произведение
.
Тогда скалярное произведение
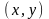 можно переписать в матричном виде:
можно переписать в матричном виде:
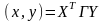 .
.
Если
{
}
− ортонормированный, то
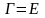 и
и
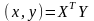 .
.
Рассмотрим
два базиса {
}
и { },
связанные при помощи матрицы перехода
},
связанные при помощи матрицы перехода
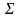 :
если
:
если
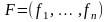 и
и
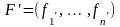
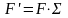 ,
т.е.
,
т.е.
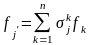 .
Тогда для базиса {
}
матрица Грама имеет вид:
.
Тогда для базиса {
}
матрица Грама имеет вид:
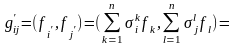
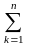
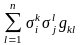 .(5)
.(5)
Эта формула даёт связь между матрицами Грама для двух связанных между собой базисов. Равенство (5) в матричном виде имеет вид:
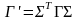
что легко проверить прямыми вычислениями.
Рассмотрим последнюю формулу в частном случае, когда { } – ортонормированный. Тогда и формула (6) имеет вид:
Г =
=
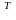
вычисляя определитель в силу теоремы об определителе произведения матриц, имеем:
detГ
=
det(
)
det
= (det
)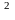 .
.
Так
как {
}
– произвольный базис
// т.к. det
 0
//
0
//
Теорема 6. Определитель матрицы Грама любого базиса положителен.
Эта теорема может быть усилена:
Теорема
7. Пусть
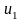 ,…,
,…,
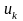 − произвольные (не обязательно линейно
независимые) вектора в евклидовом
пространстве. Тогда определитель матрицы
− произвольные (не обязательно линейно
независимые) вектора в евклидовом
пространстве. Тогда определитель матрицы
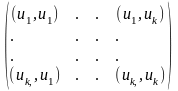 ,
,
составленной из попарных скалярных произведений, положителен, если вектора линейно независимы, и равен нулю, если они линейно зависимы.
Доказательство: Первое утверждение теоремы следует из теоремы 6, т.к. если ,…, − линейно независимы, то они образуют базис в своей линейной оболочке.
Докажем
второе утверждение. Если векторы
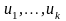 – линейно зависимы, то выполнено
равенство
– линейно зависимы, то выполнено
равенство
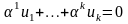 ,
где хотя бы одно
,
где хотя бы одно
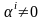 .
Умножая это равенство скалярно на каждый
из векторов
получим систему уравнений
.
Умножая это равенство скалярно на каждый
из векторов
получим систему уравнений
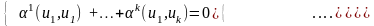 ,
,
которой
удовлетворяет ненулевое решение
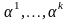 определитель матрицы этой системы равен
нулю.■
определитель матрицы этой системы равен
нулю.■
Замечание.
Доказанная теорема обобщает неравенство
Коши–Буняковского, которое имеет место
при
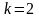 .
.
Ортогональное дополнение к линейному подпространству.
Определение
9. Два множества
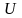 и
векторов евклидова пространства
называются ортогональными, если каждый
вектор первого множества ортогонален
к каждому вектору второго.
и
векторов евклидова пространства
называются ортогональными, если каждый
вектор первого множества ортогонален
к каждому вектору второго.
В
частности, будем говорить, что вектор
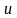 ортогонален к множеству
,
если
ортогонален каждому
ортогонален к множеству
,
если
ортогонален каждому
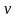 .
.
Ортогональность
и
обозначается
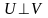 .
.
Лемма 3. Если два множества и ортогональны, то их пересечение либо пусто, либо состоит только из нулевого вектора.
Доказательство:
На самом деле, если
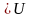 и
и
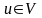
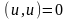
 .
■
.
■
Следствие. Сумма ортогональных подпространств всегда является прямой суммой.
Доказательство:Это следует из того, что их пересечение в силу леммы 3 состоит только из нулевого вектора сумма прямая. ■
Пусть – подпространство евклидового пространства.
Определение
10. Ортогональным дополнением подпространства
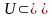 E
E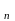 называется множество всех векторов,
перпендикулярных каждому вектору из
.
называется множество всех векторов,
перпендикулярных каждому вектору из
.
Ортогональное
дополнение к
обозначается
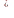 .
.
Очевидно,
что
– линейное подпространство; на самом
деле, если
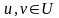 ,
а
,
а
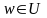 ,
то (
,
то ( u+
u+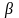 v,w)
=
(u,w)+
(v,w)
= О
u
+
v
U
,что
и требовалось доказать.
v,w)
=
(u,w)+
(v,w)
= О
u
+
v
U
,что
и требовалось доказать.
Теорема 8. Евклидово пространство есть прямая сумма любого своего подпространства U и его ортогонального дополнения U .
Доказательство:
Пусть dimU=k
и пусть e ,…,
e
,…,
e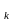 − ортонормированный базис в U.
В силу теоремы 7 из параграфа 11 (Часть
1) эти вектора можно дополнить до базиса
− ортонормированный базис в U.
В силу теоремы 7 из параграфа 11 (Часть
1) эти вектора можно дополнить до базиса
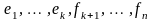 во всём пространстве
.
Применяя к ним процесс ортогонализации
Грама-Шмидта, получим ортонормированный
базис e
,…,
e
евклидова пространства
.
во всём пространстве
.
Применяя к ним процесс ортогонализации
Грама-Шмидта, получим ортонормированный
базис e
,…,
e
евклидова пространства
.
Любой элемент х Е может быть разложен по этому базису:
x
= x e
+…+
x
e
+…+
x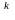 e
+
x
e
+
x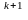 e
e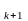 +…
+x
e
,
+…
+x
e
,
т.е.
х=x
+x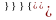 ,
где x
= x
e
+…+
x
e
U,
а x
= x
e
+…
+x
e
U
,
,
где x
= x
e
+…+
x
e
U,
а x
= x
e
+…
+x
e
U
,
в силу ортонормированности базиса. Следовательно, в силу следствия к лемме 3, сумма U и U – прямая сумма. ■
Следствие 1. (U ) = U.
Следствие
2.
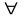 может быть единственным образом
представлен в виде х= x
+x
,
где x
U,
x
U
.
При этом x
называется ортогональной проекцией
вектора
на подпространство U,
а x
− ортогональной составляющей
относительно U.
может быть единственным образом
представлен в виде х= x
+x
,
где x
U,
x
U
.
При этом x
называется ортогональной проекцией
вектора
на подпространство U,
а x
− ортогональной составляющей
относительно U.
Задача.
В Е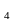 подпространство U
натянуто на векторы
подпространство U
натянуто на векторы
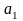 =(1,0,1,1),
и
=(1,0,1,1),
и
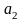 =(0,1,1,–1).
Найти ортогональную проекцию и
ортогональную составляющую вектора
=(1,2,0,1)
на подпространство U.
=(0,1,1,–1).
Найти ортогональную проекцию и
ортогональную составляющую вектора
=(1,2,0,1)
на подпространство U.
Решение. 1 способ. Вектора и − ортогональны. Нормируя их, получаем:
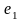 =
=
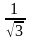 (1;0;1;1);
(1;0;1;1);
 =
(0;1;1;–1).
Если
= x
+x
+
x
=
(0;1;1;–1).
Если
= x
+x
+
x
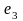 +x
+x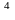
 ,
то
,
то
x
= (
,
)
=
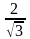 ;
x
= (
,
)
=
Если x
= x
+x
;
x
= (
,
)
=
Если x
= x
+x
x
= x
+x
= ( ;
;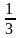 ;1;
).
;1;
).
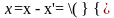 ;
;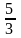 ;–1;
).
;–1;
).
2
способ. Применим процесс ортогонализации
к базису в
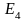 :
:
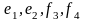 .
.
Выберем
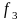 = (0;0;1;0),
= (0;0;1;0),
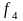 = (0;0;0;1)
ортогонализация даёт:
= (0;0;0;1)
ортогонализация даёт:
=
– (
,e
)e
– (
,e )
e
= (–
;–
;
;0)
)
e
= (–
;–
;
;0)
= (– ;– ; ;0). Аналогично, = (– ; ;0; ).
Решим
систему:
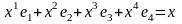
x
=
,
x
=
,
x
=-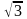 ,
x
=
x
=x
+x
;
x
=x
+x
.
,
x
=
x
=x
+x
;
x
=x
+x
.
