Задачи с решением по оптике

Интерференция света

1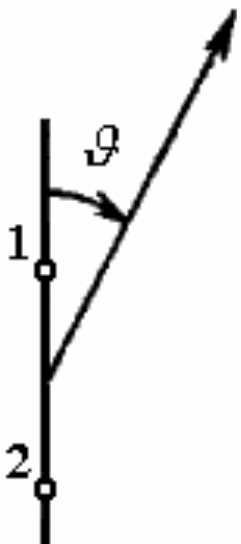 . Система (см. рис.) состоит из двух точечных когерентных излучателей 1 и 2, которые расположены в плоскости P и колеблются в направлении, перпендикулярном к этой плоскости. Расстояние между излучателями равно d, длина волны излучения – λ. Имея в виду, что колебания излучателя 2 отстают по фазе на φ от колебаний излучателя 1, найти:

а) углы , в которых интенсивность излучения максимальна;

б) условия, при которых в направлении  = π интенсивность излучения будет максимальна, а в противоположном направлении – минимальна.

Ответ: а) , k = 0,1,2,…;

б) , k = 0,1,2,…;

в) , k = 1,2,… .

2. В опыте Ллойда (см. рис.) световая волна, исходящая непосредственно из источника S (узкой щели), интерферирует с волной, отраженной от зеркала. В результате на экране Э образуется система интерференционных полос. Расстояние от источника до экрана L = 100 см. При некотором положении источника ширина интерференционной полосы на экране ∆x = 0,25 мм, а после того как источник отодвинули от плоскости зеркала на ∆h = 0,60 мм, ширина полос уменьшилась в η = 1,5 раза. Найти длину волны света.

Ответ:

3. На рис. показана интерференционная схема с бизеркалами Френеля. Угол между зеркалами α = 12', расстояния от линии пересечения зеркал до узкой щели S и экрана Э равны соответственно r = 10,0 см и b = 130 см. Длина волны света λ = 0,55 мкм. Определить:

а) ширину интерференционной полосы на экране и число возможных максимумов;

б) сдвиг интерференционной картины на экране при смещении щели на δl = 1,0 мм по дуге радиуса r с центром в точке O;

в) при какой максимальной ширине щели δ_макс интерференционные полосы на экране будут наблюдаться еще достаточно отчетливо?

О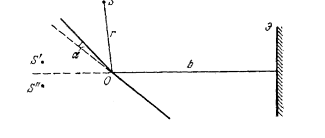 твет: а) ∆x = λ(b + r)/2αr = 1,1мм, N = 2bα/∆x + 1 = 9;

б) сдвиг картины δx = (b/r)δl = 13мм;

в) картина будет еще достаточно отчетлива, если δ≤Δx/2;

отсюда δ_макс = (1 + r/b)λ/4α = 43 мкм.

4. Плоская световая волна падает на бизеркала Френеля, угол между которыми α = 2,0'. Определить длину волны света, если ширина интерференционной полосы на экране Δx = 0,55 мм.

Ответ: λ = 2αΔx = 0,64 мкм.

5. Расстояния от бипризмы Френеля до узкой щели и экрана, равны соответственно а = 25 см и b = 100 см. Бипризма стеклянная с преломляющим углом β = 20'. Найти длину волны света, если ширина интерференционной полосы на экране Δx = 0,55 мм.

Ответ: λ = 2aβ(n – 1)Δx/(a + b) = 0,6 мкм.

6. На рис. показана схема интерферометра, служащего для измерения показателей преломления прозрачных веществ. Здесь S – узкая щель, освещаемая монохроматическим светом λ = 589 нм, 1 и 2 – две одинаковые трубки с воздухом, длина каждой из которых L = 10,0 см, Д – диафрагма с двумя щелями. Когда воздух в трубке 1 заменили аммиаком, то интерференционная картина на экране Э сместилась вверх на N = 17 полос. Показатель преломления воздуха n = 1,000277. Определить показат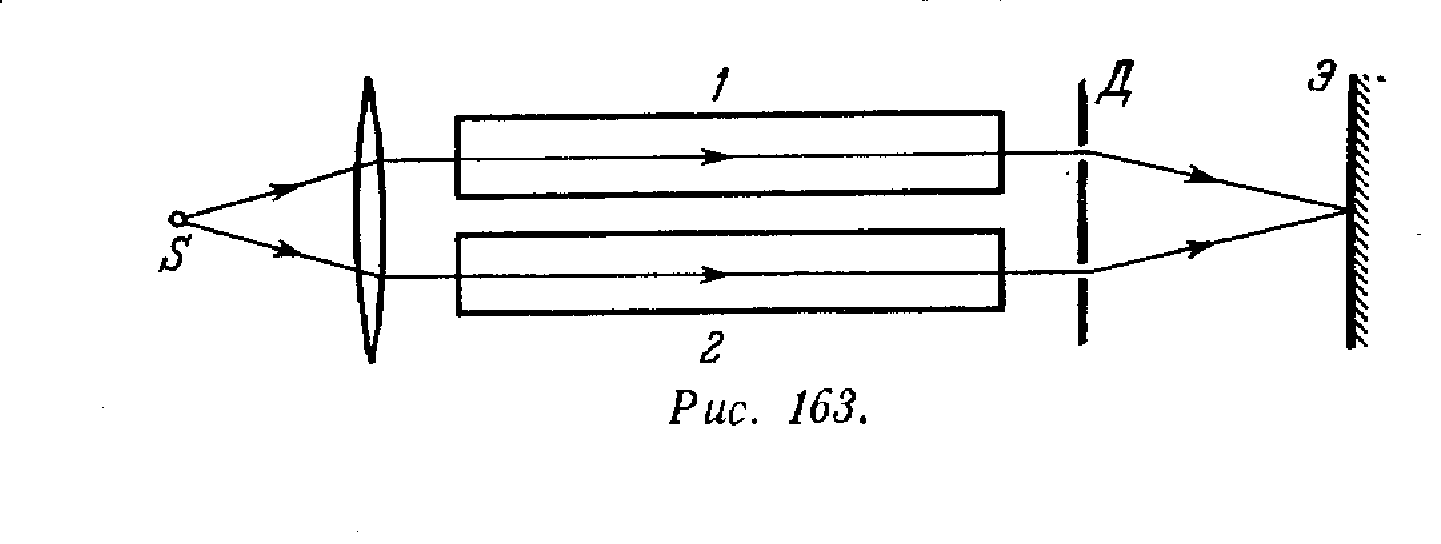 ель преломления аммиака.

Ответ: n΄ = n + Nλ/l = 1,000377.

7. На тонкую пленку (n = 1,33) падает параллельный пучок белого света. Угол падения i = 52°. При какой толщине пленки зеркально отраженный свет будет наиболее сильно окрашен в желтый цвет (λ = 0,60 мкм)?

Ответ: d = (1 + 2k)λ/4  = 0,14(1 + 2k) мкм, где k = 0, 1, 2,… .

8. Найти минимальную толщину пленки с показателем преломления 1,33, при которой свет с длиной волны 0,64 мкм испытывает максимальное отражение, а свет с длиной волны 0,40 мкм не отражается совсем. Угол падения света равен 30°.

Ответ: 0,65 мкм.

9. Рассеянный монохроматический свет с λ = 0,60 мкм падает на тонкую пленку вещества с показателем преломления n = 1,5. Определить толщину пленки, если угловое расстояние между соседними максимумами, наблюдаемыми в отраженном свете под углами с нормалью, близкими к i = 45°, равно δ = 3,0°.

Ответ: d = λ /(sin2i·δi) = 15 мкм.

10. Свет с длиной волны λ = 0,55 мкм падает нормально на поверхность стеклянного клина. В отраженном свете наблюдают систему интерференционных полос, расстояние между соседними максимумами которых Δx = 0,21 мм. Найти:

а) угол между гранями клина;

б) степень монохроматичности света (Δλ/λ), если исчезновение интерференционных полос наблюдается на расстоянии l ≈ 1,5 см от вершины клина.

Ответ: а) α = λ/2nΔx = 3΄; б) Δλ/λ ≈ Δx/l = 0,014.

11. Плосковыпуклая стеклянная линза с радиусом кривизны R = 40 см соприкасается выпуклой поверхностью со стеклянной пластинкой. При этом в отраженном свете радиус некоторого темного кольца r = 2,5 мм. Наблюдая за данным кольцом, линзу осторожно отодвинули от пластинки на Δh = 10 мк. Каким стал радиус этого кольца?

Ответ: r΄ =   = 1,5 мм.

12. На вершине сферической поверхности плосковыпуклой стеклянной линзы имеется сошлифованный плоский участок радиусом r = 3,0 мм, которым она соприкасается со стеклянной пластинкой. Радиус кривизны выпуклой поверхности линзы R = 150 см. Найти радиус шестого светлого кольца при наблюдении в отраженном свете с длиной волны λ = 655 нм

Ответ: r_k =   = 3,8 мм, k = 6.

13. Плосковыпуклая стеклянная линза с радиусом кривизны сферической поверхности R = 12,5 см прижата к стеклянной пластинке. Диаметры десятого и пятнадцатого темных колец Ньютона в отраженном свете равны d₁₀ = 1,00 мм и d₁₅ = 1,50 мм. Определить длину волны света.

Ответ: λ = (d²₁₅ – d²₁₀)/4R(k₁₅ – k₁₀) = 0,50 мкм,

где k₁₀ и k₁₅ – номера темных колец.

14. Две плосковыпуклые тонкие стеклянные линзы соприкасаются своими сферическими поверхностями. Найти оптическую силу такой системы, если в отраженном свете с λ = 0,60 мкм диаметр пятого светлого кольца d = 1,50 мм.

Ответ: Ф = 2(n – 1)(2k – 1)λ/d².

15. Две соприкасающиеся тонкие симметричные стеклянные линзы – одна двояковыпуклая, другая двояковогнутая – образуют систему с оптической силой Ф = 0,50 дп. В свете с λ = 0,61мкм, отраженном от этой системы, наблюдают кольца Ньютона. Определить:

а) радиус десятого темного кольца;

б) как изменится радиус этого кольца, если пространство между линзами заполнить водой?

Ответ: а) r =   = 3,5 мм; б) r' = r/  = 3,0 мм.

16. В двухлучевом интерферометре используется оранжевая линия ртути, состоящая из двух компонент с длинами волн λ = 576,97 нм и λ = 579,03 нм. При каком наименьшем порядке интерференции резкость интерференционной картины будет наихудшей?

Ответ: N = λ₁/2(λ₂ – λ₁) = 140.

17. В интерферометре Майкельсона использовалась желтая линия натрия, состоящая из двух компонент с длинами волн λ = 589,0 нм и λ = 589,6 нм. При поступательном перемещении одного из зеркал интерференционная картина периодически исчезала (почему?). Найти перемещение зеркала между двумя последовательными исчезновениями интерференционной картины.

Ответ: h = λ²/2Δλ = 0,3 мм.