Львівський національний університет імені Івана Франка
«
Н Кафедра механіки
ЛАБОРАТОРНА РОБОТА № 9
СУМІСНА ДІЯ ЗГИНУ З КРУЧЕННЯМ
Виконав(ла) студент(ка) групи Мх___
__________________________________
Перевірив_________________________
Львів – 2010
§1 Вихідні співвідношення
ВИЗНАЧЕННЯ ВЕЛИЧИНИ І НАПРЯМКУ ГОЛОВНИХ НАПРУЖЕНЬ
Визначимо величину
і напрямок головних напружень на поверхні
круглого
стрижня
довжиною
,
один кінець якого затиснутий, а до
другого кінця прикладена сила, яка
знаходиться на деякій
віддалі
від його осі і є перпендикулярною до
неї (рис. 1).
Рис. 1
Якщо силу
паралельно перенести в точку
осі стрижня, то
для того щоб система
сил, що діє на стрижень була еквівалентною,
потрібно додати крутний момент
:
.
Отже, розрахункова схема матиме вигляд (рис.2):
Рис. 2
Розглянемо
поперечний переріз
стрижня з
координатою
,
в
якому
буде виникати згинаючий момент
і крутний момент
,
тобто в цьому перерізі в точці
(рис.
3) діятимуть
максимальні нормальні
напруження
,
від дії
згинаючого моменту
(1)
і максимальні
дотичні напруження
,
від дії крутного моменту. (2)
Рис. 3
У
формулах
(1)
і (2)
– момент
опору при
згині, а
– момент опору при крученні,
які пов’язані
залежністю: 
.
(3)
Виділимо поблизу
точки
призматичний елемент і вкажемо, які
напруження будуть діяти на його гранях,
причому ребро
є паралельне осі стрижня (рис.4).
Рис.4
На гранях
і
будуть діяти як нормальні напруження
,
так і дотичні напруження
.
На гранях
і
будуть діяти тільки дотичні напруження
(закон парності дотичних напружень).
Грані
і
є вільні від напружень. Отже,виділений
елемент знаходиться в умовах плоского
напруженого стану
(рис.5):
Рис.5
Зауважимо, що на рис.5 вказаний додатній напрямок дотичних напружень.
Згідно [1,2], за допомогою круга Мора можемо знайти величину і напрямок головних напружень (рис.6):
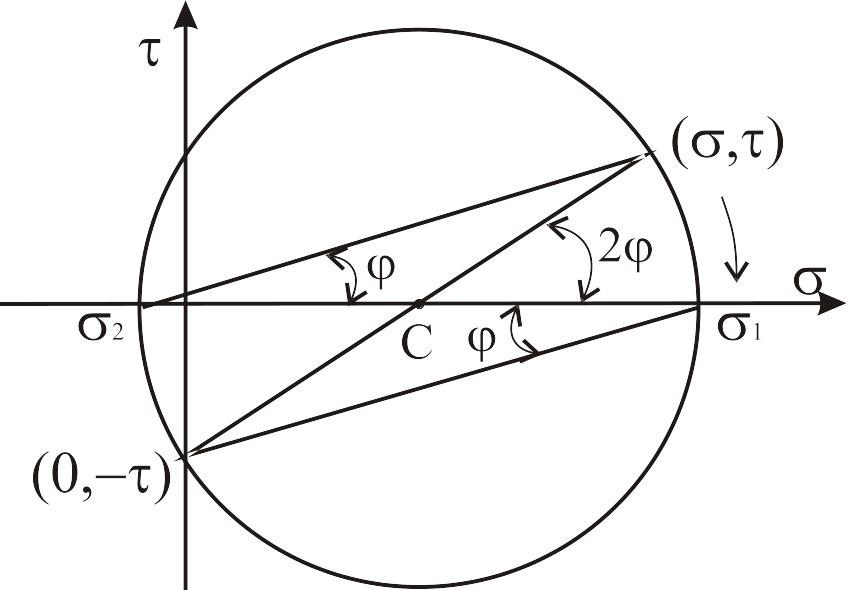
Рис.6
Як видно з рис. 6:
,
,
тому
величина і напрямок головних напружень,
тобто кут
знайдемо
за формулами:
,
,
(4)
.
Якщо врахувати залежності (1) – (3), то формули (4) можемо записати у такому вигляді:
,
,
(5)
.
Величину
і напрямок головних напружень,
також можемо знайти
експериментально за допомогою прямокутної
розетки тензодатчиків
(рис.7а):
Рис. 7а
(6)
чи дельта
(
)-розетки
(рис.7б):
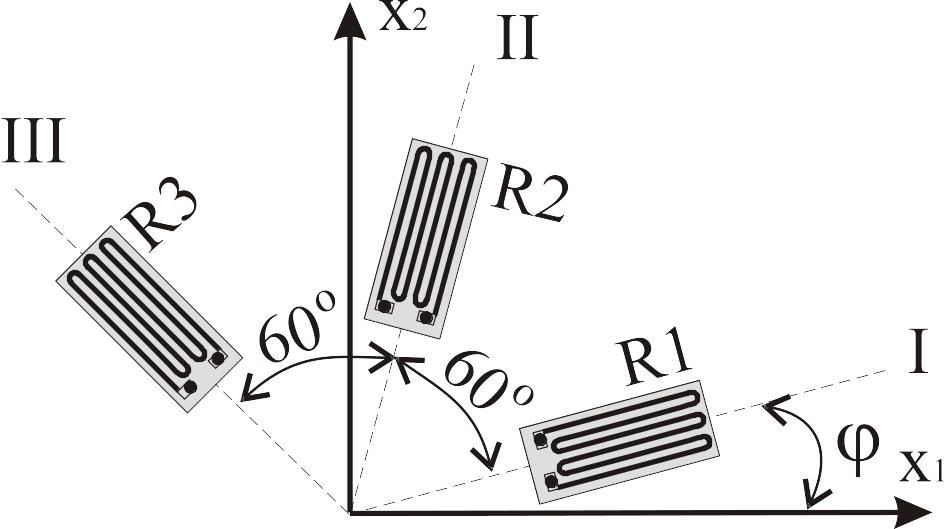
Рис. 7б
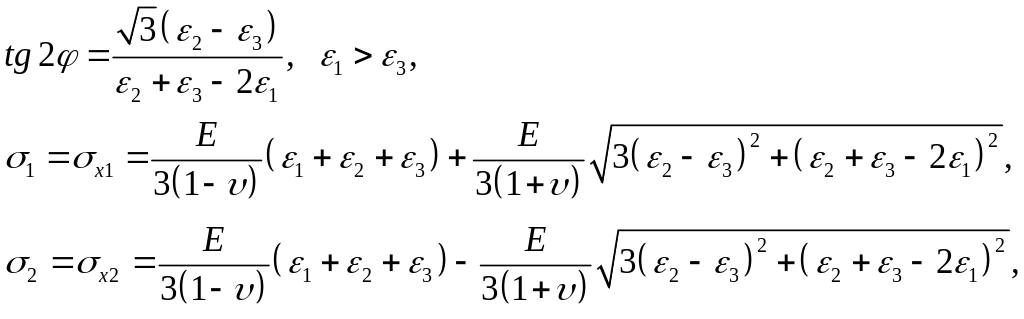(7)
де
–
відповідно
модуль Юнга
і коефіцієнт
Пуасона
матеріалу,
з якого виготовлений стрижень,
–
деформація
у
відповідному
напрямку,
яка
визначається
за допомогою
-тензодатчика,
кут
характеризує
напрямок
головного напруження
по відношенню до напрямку першого
тензодатчика розетки.
Формули (5), (6), (7) є вихідними при виконанні даної роботи, відповідно при теоретичному і експериментальному знаходженні величини і напрямку головних напружень.
Зауважимо, шо якщо реалізувати відповідне закріплення в точці ,тобто, щоб стрижень працював тільки на кручення, то згідно (4), (2) будемо мати:
,
.
(8)
Отримані тереотичні результати (5) можна перевірити за допомогою експериментальних даних використовуючи формули (6) чи (7).