Кубическая парабола

Кубическая парабола задается функцией  . Вот знакомый со школы чертеж:

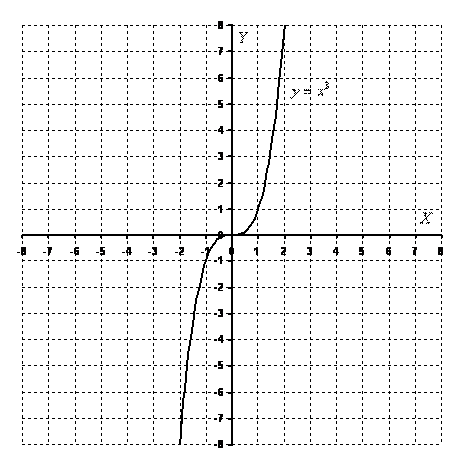Перечислим основные свойства функции 

Область определения – любое действительное число: .

Область значений – любое действительное число: .

Функция   является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием  . Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»:  , значит, функция   является нечетной.

Функция   не ограничена. На языке пределов функции это можно записать так:  ,  Кубическую параболу тоже эффективнее строить с помощью Анфисы Чеховой алгоритма «челнока»:

Наверняка, вы заметили, в чем ещё проявляется нечетность функции. Если мы нашли, что  , то при вычислении   уже не нужно ничего считать, автоматом записываем, что  . Эта особенность справедлива для любой нечетной функции.

Теперь немного поговорим о графиках многочленов.

График любого многочлена третьей степени   ( ) принципиально имеет следующий вид:

В этом примере коэффициент при старшей степени  , поэтому график развёрнут «наоборот». Принципиально такой же вид имеют графики многочленов 5-ой, 7-ой, 9-ой и других нечетных степеней. Чем выше степень, тем больше промежуточных «загибулин».

Многочлены 4-ой, 6-ой и других четных степеней имеют график принципиально следующего вида:

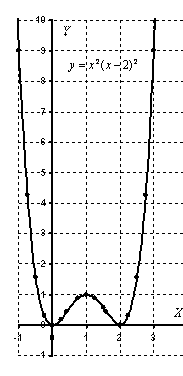Эти знания полезны при исследовании графиков функций.

График функции

Выполним чертеж:

Основные свойства функции  :

Область определения: .

Область значений:  .

То есть, график функции полностью находится в первой координатной четверти.

Функция   не ограничена сверху. Или с помощью предела: 

При построении простейших графиков с корнями также уместен поточечный способ построения, при этом выгодно подбирать такие значения «икс», чтобы корень извлекался нацело:

На самом деле хочется разобрать еще примеры с корнями, например,  , но они встречаются значительно реже. Я ориентируюсь на более распространенные случаи, и, как показывает практика, что-нибудь вроде   приходиться строить значительно чаще. Если возникнет необходимость выяснить, как выглядят графики с другими корнями, то, рекомендую заглянуть в школьный учебник или математический справочник.

График гиперболы

Опять же вспоминаем тривиальную «школьную» гиперболу  .

Выполним чертеж: Основные свойства функции  :

Область определения: .

Область значений:  .

Запись   обозначает: «любое действительное число, исключая ноль»

В точке   функция терпит бесконечный разрыв. Или с помощью одностороннихпределов:  ,  . Немного поговорим об односторонних пределах. Запись   обозначает, что мы бесконечно близко приближаемся по оси   к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси  . Именно этот факт и записывается пределом  . Аналогично, запись   обозначает, что мы бесконечно близко приближаемся по оси   к нулю справа.  При этом ветвь гиперболы уходит вверх на плюс бесконечность,бесконечно близко приближаясь к оси  . Или коротко:  .

Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.

В данном случае ось   является вертикальной асимптотой для графика гиперболы при  .

Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.

Также односторонние пределы  ,   говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.

Исследуем функцию на бесконечности:  , то есть, если мы начнем уходить  по оси   влево (или вправо) на бесконечность, то  «игреки» стройным  шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близкоприближаться к оси  .

Таким образом, ось   является горизонтальной асимптотой для графика функции , если «икс» стремится к плюс или минус бесконечности.

Функция   является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически:  .

График функции вида   ( ) представляют собой две ветви гиперболы.

Если  , то гипербола расположена в первой и третьей координатных четвертях(см. рисунок выше).

Если  , то гипербола расположена во второй и четвертой координатных четвертях.

Пример 3

Построить правую ветвь гиперболы 

Используем поточечный метод построения, при этом, значения   выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.