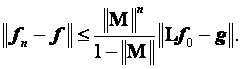Метод последовательных приближений
Мощным
средством решения уравнения 
является
метод, основанный на построении
последовательности операторов 
,
которые в некотором смысле все лучше и
лучше
приближают оператор 
. Этот метод носит название метода
последовательных приближений.
По существу, оператор
интерпретируется
как предел некоторой последовательности
операторов, и эта последовательность
строится в ходе решения задачи. Для того
чтобы придать смысл всем этим интуитивным
соображениям, требуется определить
понятие сходимости операторов и степень
близости их друг к другу. Один из подходов
основан на придании множеству операторов
структуры банахова пространства и
использовании свойств этого пространства.
Пусть V и W –
векторные пространства, а 
и 
–
линейные операторы, 
.
Определим оператор 
, называемый суммой операторов 
и
, как
и
оператор 
,
называемый произведением оператора на число, как
Нулевой
оператор обозначим через O,
а полученное векторное пространство
линейных операторов – через L
.
Если
рассматриваются операторы,
отображающие V в V,
то векторное пространство таких
операторов можно обозначить через L
.
Тот факт, что оператор L из L
имеет
обратный оператор, можно записать как
существование оператора 
L
(обратите
внимание на порядок следования
пространств V и W).
Теперь, когда мы построили векторное
пространство линейных операторов (а
значит, можем рассматривать линейный
оператор как вектор или точку этого
пространства), естественно сделать
попытку ввести на этом пространстве
норму, чтобы иметь возможность оценивать
близость точек пространства друг к
другу. Попробуем определить норму
оператора, обобщив уже известное нам
понятие равномерной нормы вектора
(функции). Рассмотрим оператор 
,
и пусть 
, 
,
где B и C –
банаховы пространства (мы выбираем
здесь банаховы пространства потому,
что нам нужно, чтобы векторы из 
и 
обладали
нормой). Оператор L отображает
точку f из
в
точку Lf из
.
Назовем этот оператор ограниченным,
если существует такое число 
,
что
|
(4.27) |
(первая
норма – в векторном пространстве C,
а вторая – в B).
Если оператор L не
ограничен на
,
то он называется неограниченным.
Очевидно, для каждой точки 
существует
некое минимальное значение m,
для которого справедливо неравенство
(4.27) (разумеется, если L –
ограниченный оператор). Максимальное
же значение таких m,
при котором неравенство (4.27) справедливо
во всех точках
,
мы будем называть нормой
оператора L и
обозначать 
.
В случае линейных операторов вопрос об их ограниченности решается следующей теоремой.
Теорема. Линейный оператор L из B в C ограничен на тогда и только тогда, когда он непрерывен.
Далее
под L
мы
будем понимать векторное пространство
линейных ограниченных операторов.
Разберем
пример. Пусть 
− n‑мерный
линейный оператор, который, как мы уже
знаем, в базисе 
может
быть задан матрицей
Предположим,
что 
наделено
нормой 
,
тогда
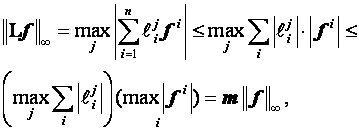
где 
.
Отсюда 
.
Покажем, что 
.
Попробуем найти такое 
,
для которого 
.
Из определения m видно,
что существует такое целое k,
при котором 
.
В качестве
выберем
вектор с нормой, равной единице, и
координатами 
.
Тогда цепочка неравенств обращается в
равенства
и в итоге мы получаем требуемый результат.
Введенная
выше норма оператора задает на L
структуру
банахова пространства. Покажем, что
пространство L
является
полным по операторной норме. Выберем
последовательность Коши операторов 
L
и
покажем, что предел этой последовательности
также лежит в L
.
1. Так
как 
–
последовательность Коши, то 
при 
;
значит, последовательность 
,
где 
и 
,
также образует последовательность
Коши, поскольку
Но
раз C полно,
то 
.
2. Пусть 
.
Очевидно, что L –
линейный оператор. Убедимся, что он
ограничен. Действительно,
Но так как
то 
тоже
образует последовательность Коши в 
.
Обозначим 
,
тогда
3. Осталось
показать, что 
,
то есть что
Поскольку 
–
последовательность Коши, то для
любого 
найдется
номер N,
такой, что если 
,
то 
. Тогда
при
имеем 
и
что
справедливо для любого
.
Отсюда 
,
а поскольку 
произвольно,
то
Вернемся, однако, к построению обратного оператора методом последовательных приближений. Идея метода очень проста. Представим оператор L в виде
,
где I – тождественный оператор, а M – некий линейный оператор, тогда
или
|
(4.28) |
Для нахождения f организуем следующую итерационную процедуру. В качестве нулевого приближения f возьмем точку g, то есть
Далее, подставляя нулевое приближение в правую часть уравнения (4.28), получим первое приближение
Продолжая аналогично, мы можем получить любое n-е приближение по следующей рекуррентной формуле:
|
(4.29) |
Распишем формулу (4.29), подставив в нее предыдущее приближение:
|
(4.30) |
В
последнем выражении у нас получился
некий новый оператор, который мы будем
называть степенью
оператора.
Это частный случайпроизведения
операторов.
Если 
,
– линейные операторы и 
–
векторные пространства, то произведением
операторов NL называется
оператор 
,
ставящий в соответствие элементу 
элемент
.
Область
определения 
есть
множество элементов 
,
таких, что 
.
Если L и N –
ограниченные операторы и 
–
нормированные пространства, то
оператор 
также ограничен и
|
(4.31) |
.
Действительно,
для любого
,
а значит и 
по
определению нормы оператора имеем
.
Аналогично
для любого 
.
Поскольку , то получаем
Отсюда
в соответствии с определением нормы
оператора следует неравенство (4.31).
Если 
,
то произведение NN будем
называтьстепенью
оператора и
обозначать 
.
Точно так же можно определить любую
целую степень оператора. Естественно
считать, что 
.
Таким образом, выражение (4.30) для 
можно
записать через степень оператора M:
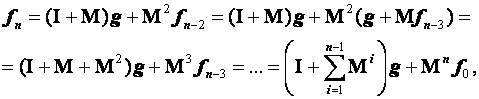
или
учитывая, что 
,
а 
,
Мы
ожидаем, что 
и
|
(4.32) |
Если
для оператора L существует
обратный оператор
,
то 
, и
значит
|
(4.33) |
.
Все
это, однако, формальные построения, ибо
нет уверенности в том, что ряд (4.32)
сходится. Посмотрим, при каких же условиях
это происходит, то есть в каком случае
метод последовательных приближений
работает. Пусть B –
банахово пространство и 
L
,
а значит, и 
L
.
Требуется выяснить, когда 
существует
или, иначе говоря, 
L
.
Последнее означает, что оператор L имеет
ограниченный обратный оператор, то
есть 
.
Из формулы (4.33) имеем
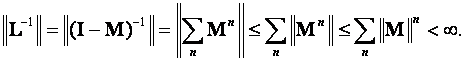
Ряд 
–
уже числовой (а именно, геометрическая
прогрессия), относительно которого
известно, что он сходится, если 
.
Это и есть условие сходимости ряда
(4.32). Легко установить, что
при
последовательность 
имеет
предел
.
Из уравнений
следует, что
|
|
|
(4.34) |
Откуда при вытекает:
Неравенство (4.34) характеризует скорость сходимости итерационной процедуры метода последовательных приближений. Но поскольку fнеизвестно, эту оценку надо переформулировать. Из уравнения
следует, что
Откуда
Подставляя этот результат в (4.34), получим окончательно
|
(4.35) |
Величина 
в
неравенстве (4.35) – норма невязки нулевого
приближения – легко вычисляется,
поэтому не составляет труда, зная 
,
вычислить необходимое для достижения
заданной точности число итераций.
Интересно
рассмотреть действие оператора M и
условие
с
геометрической точки зрения. Пусть L,
а следовательно и M,
отображают банахово пространство в
себя: 
(в
противном случае мы не сможем ввести
степень оператора). Тогда 
–
точки одного и того же пространства B.
Расстояние между двумя соседними точками
последовательности
определяется
нормой их разности 
.
Посмотрим, как меняется это расстояние
с ростом n,
или, что то же, под действием оператора M.
Выразим расстояние между точками 
и 
через
расстояние между точками
и 
.
Поскольку
получаем
Если 
,
то очевидно, что расстояние между двумя
последовательными точками сокращается
с ростом n точки
сближаются. При 
расстояния
между соседними точками могут расти.
Если
,
то оператор M называют оператором
сжатия.
Точное определение таково. Говорят, что
оператор A удовлетворяет условию
Липшица на 
с
константой (Липшица) q,
если существует такое 
,
что
, 
.
Если 
,
то оператор A называется оператором
сжатия (или сжимающим).
Термин этот очень нагляден, что вполне
подтверждается геометрической
иллюстрацией действия оператора M.
В заключение этого параграфа рассмотрим
часто используемое приложение метода
последовательных приближений к решению
систем линейных алгебраических уравнений
и ограничения, вытекающие из условия
.
Пусть требуется решить уравнение
|
(4.36) |
,
где
оператор 
,
обычно записываемый в виде
квадратной 
матрицы
(в соответствующем ортонормированном
базисе), а 
–
векторы неизвестных и правых частей
соответственно. Представим оператор A в
виде 
,
где I –
единичная матрица, а M –
некая новая матрица (оператор). Пусть 
–
элементы матрицы A,
тогда числа 
будут
элементами матрицы M (
–
символ Кронекера). Уравнение (4.36) запишется
в виде
.
Если , мы можем организовать итерационную процедуру
и
вычислить 
.
Это хорошо известный метод решения
систем линейных уравнений – метод
Якоби.
Выясним, какие ограничения на элементы
матрицы A накладывает
требование
.
Будем работать с нормой 
, тогда
.
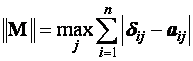Так
как
, то,
очевидно, что 
для
любого j,
то есть
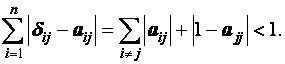
Откуда
или каждый диагональный элемент по модулю должен быть больше суммы модулей всех остальных элементов в данном столбце. Это хорошо известное условие сходимости метода Якоби – условие диагонального преобладания матрицы A.
26.Транспортная задача. Сущность транспортной задачи Транспортная задача является представителем класса задач линейного программирования и поэтому обладает всеми качествами линейных оптимизационных задач, но одновременно она имеет и ряд дополнительных полезных свойств, которые позволили разработать специальные методы ее решения. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение.
Под термином «транспортные задачи» понимается широкий круг задач не только транспортного характера. Общим для них является, как правило, распределение ресурсов, находящихся у m производителей (поставщиков), по n потребителям этих ресурсов. Различают два типа транспортных задач: но критерию стоимости (план перевозок оптимален, если достигнут минимум затрат на его реализацию) и по критерию времени (план оптимален, если на его реализацию затрачивается минимум времени).
Наиболее часто встречаются следующие задачи, относящиеся к транспортным:
- прикрепление потребителей ресурса к производителям;
- привязка пунктов отправления к пунктам назначения;
- взаимная привязка грузопотоков прямого и обратного направлений;
- отдельные задачи оптимальной загрузки промышленного оборудования;
- оптимальное распределение объемов выпуска промышленной продукции между заводами-изготовителями и др.
где n - количество пунктов отправления,
m - количество пунктов назначения,
аi - запас продукции в пункте отправления Ai() [ед. прод.],
bj - спрос на продукцию в пункте назначения Bj() [ед. прод.],
cij - тариф (стоимость) перевозки единицы продукции из пункта отправления Ai в пункт назначения Bj [руб. / ед. прод.],
xij - количество продукции, перевозимой из пункта отправления Ai в пункт назначения Bj [ед. прод.],
L(Х) - транспортные расходы на перевозку всей продукции [руб.].
Целевая функция представляет собой общие транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте.
Рассмотрим экономико-математическую модель прикрепления пунктов отправления к пунктам назначения. Имеются m пунктов отправления груза и объемы отправления по каждому пункту a1, a2 ,...,am . Известна потребность в грузах b1, b2 ,...,bn по каждому из n пунктов назначения. Задана матрица стоимостей доставки по каждому варианту cij , . Необходимо рассчитать оптимальный план перевозок, т.е. определить, сколько груза должно быть отправлено из каждого i-го пункта отправления (от поставщика) в каждый j-ый пункт назначения (до потребителя) xij с минимальными транспортными издержками.
В общем виде исходные данные представлены в табл. 3.1. Строки транспортной таблицы соответствуют пунктам отправления (в последней клетке каждой строки указан объем запаса продукта ai ), а столбцы -- пунктам назначения (последняя клетка каждого столбца содержит значение потребности bj). Все клетки таблицы (кроме тех, которые расположены в нижней строке и правом столбце) содержат информацию о перевозке из i-го пункта в j-й: в правом верхнем углу находится цена перевозки единицы продукта, а в левом нижнем -- значение объема перевозимого груза для данных пунктов.
Исходные данные
Транспортная задача называется закрытой, если суммарный объем отправляемых грузов равен суммарному объему потребности в этих грузах по пунктам назначения :
Если такого равенства нет (потребности выше запасов или наоборот), запасу называют открытой, т.е.:
Для написания модели необходимо все условия (ограничения) и целевую функцию представить в виде математических уравнении.
Все грузы из i-х пунктов должны быть отправлены, т.е.
Все j-е пункты (потребители) должны быть обеспечены грузами в плановом объеме:
Суммарные объемы отправления должны равняться суммарным объемам назначения. Должно выполняться условие не отрицательности переменных. Перевозки необходимо осуществить с минимальными транспортными издержками (функция цели):
Вместо матрицы стоимостей перевозок (cij) могут задаваться матрицы расстояний. В таком случае в качестве целевой функции рассматривается минимум суммарной транспортной работы. Как видно из выражения (3.1), уравнение баланса является обязательным условием решения транспортной задачи. Поэтому, когда в исходных условиях дана открытая задача, то ее необходимо привести к закрытой форме. В случае, если
- потребности по пунктам назначения превышают запасы пунктов отправления, то вводится фиктивный поставщик с недостающим объемом отправления;
- запасы поставщиков превышают потребности потребителей, то вводится фиктивный потребитель с необходимым объемом потребления.
Варианты, связывающие фиктивные пункты с реальными, имеют нулевые оценки. После введения фиктивных пунктов задача решается как закрытая.
Транспортным задачам присущи следующие особенности:
- распределению подлежат однородные ресурсы;
- условия задачи описываются только уравнениями;
- все переменные выражаются в одинаковых единицах измерения;
- во всех уравнениях коэффициенты при неизвестных равны единице;
- каждая неизвестная встречается только в двух уравнениях системы ограничений.
Транспортные задачи могут решаться симплекс-методом. Однако перечисленные особенности позволяют для транспортных задач применять более простые методы решения.
Опорный план является допустимым решением транспортной задачи и используется в качестве начального базисного решения при нахождении оптимального решения методом потенциалов. Существует три метода нахождения опорных планов: метод северо-западного угла, метод минимального элемента и метод Фогеля. «Качество» опорных планов, полученных этими методами, различается: в общем случае метод Фогеля дает наилучшее решение (зачастую оптимальное), а метод северо-западного угла - наихудшее.
Все существующие методы нахождения опорных планов отличаются только способом выбора клетки для заполнения. Само заполнение происходит одинаково независимо от используемого метода.
1. Диагональный метод, или метод северо-западного угла. При этом методе на каждом шаге построения первого опорного плана заполняется левая верхняя клетка (северо-западный угол) оставшейся части таблицы. При таком методе заполнение таблицы начинается с клетки неизвестного x11 и заканчивается в клетке неизвестного xmn, т. е. идет как бы по диагонали таблицы перевозок.
2. Метод наименьшей стоимости. При этом методе на каждом шаге построения опорного плана первою заполняется та клетка оставшейся части таблицы, которая имеет наименьший тариф. Если такая клетка не единственная, то заполняется любая из них Замечание. В диагональном методе не учитываются величины тарифов, в методе же наименьшей стоимости эти величины учитываются, и часто последний метод приводит к плану с меньшими общими затратами, хотя это и не обязательно..
Кроме рассмотренных выше способов иногда используется, так называемый метод Фогеля. Суть его состоит в следующем: в распределительной таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Отмечается наибольшая разность. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейшем в расчет не принимаются. На каждом этапе загружается только одна клетка. Распределение груза производится, как и ранее.
Существующий алгоритм решения транспортных задач (метод потенциалов) предполагает, что целевая функция стремится к минимуму. Однако существуют ситуации, когда в рамках транспортной модели требуется максимизировать целевую функцию, например, общий доход, объем продаж, прибыль, качество выполняемых работ и т.д.
В этом случае в модель вместо искомой целевой функции L(Х) вводится целевая функция
L1(X)=-L(Х),
в которой тарифы умножаются на (-1). Таким образом, максимизация L(Х) будет соответствовать минимизации L1(Х) [2]. Если в задаче идет речь о том, что из каждого пункта отправления можно перевозить продукцию нескольких видов, то при построении модели можно использовать один из следующих вариантов:
- каждому виду продукции должна соответствовать одна транспортная матрица;
все виды продукции представлены в одной общей матрице с использованием запрещающих тарифов в клетках, связывающих разные виды продукции.
Транспортная задача.