- •Учебно – методические материалы по физике Составитель: старший преподаватель межфакультетской кафедры гуманитарных и естественнонаучных дисциплин Смирнова л.А.
- •1. Общие требования к оформлению
- •2. Практическая работа № 1
- •2.1. Методические указания
- •2.2. Основные законы и формулы. Примеры решения задач
- •2.2.1. Кинематика поступательного и вращательного движения
- •Примеры решения задач
- •2.2.2. Динамика. Законы Ньютона
- •Примеры решения задач
- •2.2.3. Работа постоянной и переменной силы. Закон сохранения механической энергии
- •Примеры решения задач
- •Задача 3
- •2.2.4. Закон сохранения импульса. Совместное применение законов сохранения импульса и механической энергии
- •Примеры решения задач
- •2.2.5. Динамика вращательного движения твёрдого тела
- •Примеры решения задач
- •2.2.6. Закон сохранения момента импульса. Кинетическая энергия вращающегося тела
- •Примеры решения задач
- •2.2.7. Элементы специальной теории относительности
- •Примеры решения задач
- •2.3. Задачи «Практическая работа № 1»
- •3. Практическая работа № 2
- •3.1. Методические указания к выполнению практической работы № 2
- •3.2. Основные законы и формулы. Примеры решения задач
- •3.2.1. Идеальный газ. Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)
- •Примеры решения задач
- •3.2.2. Основное уравнение молекулярно-кинетической теории газов. Внутренняя энергия идеального газа
- •Примеры решения задач
- •3.2.3. Элементы классической статистики
- •Примеры решения задач
- •3.2.4. Первое начало термодинамики. Теплоёмкость идеального газа
- •Примеры решения задач
- •Работа газа, нагреваемого при постоянном объеме, равна нулю
- •3.2.5. Круговые процессы. Кпд цикла. Цикл Карно
- •Примеры решения задач
- •3.2.6. Энтропия
- •Примеры решения задач
- •3.3. Задачи «Практическая работа №2»
- •4. Практическая работа № 3
- •4.1. Методические указания к выполнению к практической работы № 3
- •4.2. Основные законы и формулы. Примеры решения задач
- •4.2.1.Электростатика
- •Примеры решения задач
- •Таким образом,
- •Произведя вычисления, получим:
- •4.2.2. Постоянный электрический ток
- •Примеры решения задач
- •Откуда получаем
- •4.2.3. Магнитостатика
- •Примеры решения задач
- •Из рис. 6 следует, что
- •4.2.4. Электромагнитная индукция
- •Примеры решения задач
- •Максимальное значение эдс индукции равно
- •Учитывая формулу (2), получим:
- •Энергия магнитного поля соленоида
- •4.3. Задачи «Практическая работа № 3»
- •5. Практическая работа № 4
- •5.1. Методические указания к выполнению практической работы № 4
- •5.2. Основные законы и формулы. Примеры решения задач
- •5.2.1. Гармонические механические колебания
- •Примеры решения задач
- •5.2.2. Затухающие колебания
- •Примеры решения задач
- •5.2.3. Электромагнтные колебания
- •Примеры решения задач
- •5.2.4. Сложение гармонических колебаний
- •Примеры решения задач
- •5.2.5. Упругие и электромагнитные волны
- •Примеры решения задач
- •5.2.6. Интерференция света
- •Примеры решения задач
- •5.2.7. Дифракция света
- •Примеры решения задач
- •5.2.8. Поляризация света
- •Примеры решения задач
- •5.3. Задачи «Практическая работа № 4»
- •6. Практическая работа № 5
- •6.1. Методические указания к выполнению практической работы № 5
- •6.2. Основные законы и формулы. Примеры решения задач
- •6.2.1. Тепловое излучение
- •Примеры решения задач
- •6.2.2. Фотоэффект
- •6.2.3. Физика атома. Спектры атомов
- •Примеры решения задач
- •6.2.4. Элементы квантовой механики
- •Примеры решения задач
- •6.2.5.Физика твердого тела
- •Примеры решения задач
- •6.2.6. Физика атомного ядра. Радиоактивность
- •Примеры решения задач
- •6.3. Задачи «Практическая работа № 5»
- •Приложения
- •2. Некоторые астрономические величины (округленные значения)
- •3. Относительные атомные массы некоторых элементов
- •4. Масса, заряд и энергия покоя некоторых частиц
- •5. Относительная диэлектрическая проницаемость
- •6. Удельное сопротивление металлов
- •7. Показатели преломления
- •8. Работа выхода электрона из металла
- •9. Электрические характеристики некоторых полупроводников (температура комнатная)
- •10. Характеристики некоторых радиоактивных изотопов
- •11. Массы атомов некоторых химических элементов
- •12. Некоторые соотношения между единицами измерения физических величин
- •12. Множители и приставки для образования десятичных кратных и дольных единиц и их наименования
- •13. Греческий алфавит
6.2.3. Физика атома. Спектры атомов
1. Полная энергия электрона в состоянии, характеризуемом главным квантовым числом n
![]() ,
(3)
,
(3)
где Ei = Rhc – энергия ионизации атома водорода; Z – порядковый номер элемента в таблице Менделеева; Еi = 13,5 эВ.
2. Энергия, излучаемая или поглощаемая атомом водорода или водородоподобным ионом
E
= h
![]() ,
,
где n1 и n2 – главные квантовые числа, соответствующие энергетическим состояниям, между которыми совершается переход электрона.
3. Сериальная формула для определения длины волны спектра излучения атома водорода (или водородоподобного иона)
![]() =
RZ2
=
RZ2![]() ,
,
где – длина волны фотона; R – постоянная Ридберга.
Примеры решения задач
Задача 1
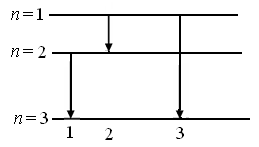
Атом водорода перешел из возбужденного состояния, характеризуемого главным квантовым числом, равным трем, в основное. Определить возможные спектральные линии в спектре излучения водорода. Найти максимально возможную энергию фотона.
Дано: |
Решение: |
n1 = 1 n2 = 3 |
n
= 3
n
= 2
n
= 1 Рис. 1 |
- ?
|
Из рисунка видно, что при переходе атома из состояния, характеризуемого главным квантовым числом n = 3, в основное (n = 1), возможно излучение трех спектральных линий.
Для определения длины волны воспользуемся сериальной формулой для водородоподобных ионов
![]() ,
,
где – длина волны фотона; R – постоянная Ридберга; Z – заряд ядра в относительных единицах (при Z = 1 формула переходит в сериальную формулу для водорода); n1 – главное квантовое число состояния, в которое перешел атом; n2 – главное квантовое число исходного состояния.
Найдем
длину волны линии, излученной при
переходе атома из состояния
n2 =
3 в состояние n1
= 2, приняв
постоянную Ридберга
![]() м-1:
м-1:
![]() ,
,
![]() мкм.
мкм.
Аналогично находим длину волны спектральной линии, излученной атомом при переходе из состояния n2 = 2 в состояние n1 = 1.
![]() ,
,
![]() мкм.
мкм.
При переходе из состояния n2 = 3 в состояние n1 = 1 длина волны линии равна
![]() ,
,
![]() мкм.
мкм.
Энергия фотона определяется из выражения
ф = hc/ ,
где
h
– постоянная
Планка, h
=
![]() 10-34
Дж
10-34
Дж![]() ,
с – скорость света в вакууме, с =
108м/с.
,
с – скорость света в вакууме, с =
108м/с.
Максимальная энергия фотона соответствует минимальной длине волны, следовательно
ф
= hc/![]() .
.
6.2.4. Элементы квантовой механики
1. Длина волны де Бройля
![]() ,
,
где p – импульс частицы.
2. Если кинетическая энергия частицы много меньше энергии покоя (Еk << E0), то для определения импульса частиц можно пользоваться классическим выражением, т.е.
p
= mv
=
![]() ,
,
где
кинетическая энергия частицы
![]() .
.
3. Если кинетическая энергия частицы Ek E0, то импульс частицы следует вычислять по формуле релятивистской механики, т.е.
![]() ,
,
где Ео – энергия покоя частицы; Ек – кинетическая энергия частицы, равная
Ек
= m0c2 ,
,
где m0 – масса покоя частицы; v – скорость частицы.
4. Соотношения неопределенностей:
а) для координаты и импульса ∆px∆x≥ћ/2,
где
![]() – неопределенность проекции импульса
на ось x;
– неопределенность проекции импульса
на ось x;
– неопределенность координаты x;
б) для энергии и времени ∆E∆t≥ћ/2,
где
![]() – неопределенность энергии;
– неопределенность энергии;
![]() t
– время жизни квантовой системы в данном
энергетическом состоянии.
t
– время жизни квантовой системы в данном
энергетическом состоянии.