Правило прецессии

В силу общего закона динамики вращательного движения ( , т.е. изменение главного кинетического момента определяется выражением ) любой внешний момент, вектор которого не совпадает по направлению с вектором , изменяет положение вектора главного кинетического момента гироскопа с угловой скоростью прецессии:

,

где:  проекция вектора внешнего момента на экваториальную плоскость ротора гироскопа (плоскость, проходящая через точу О и перпендикулярная вектору ), равная .

Как было показано выше, движение с угловой скоростью прецессии происходит таким образом, чтобы совместить вектор с вектором по кратчайшему пути.

Правило гироскопической реакции

При действии на гироскоп, обладающий кинетическим моментом , переносной угловой скорости возникает момент гироскопической реакции:

,

где: ,

вектор момента гироскопической пары направлен так, что совмещает по кратчайшему пути вектор (вектор совпадает по направлению с вектором ) с вектором .

.

Направление гироскопических сил ищется с помощью правила Н.Е. Жуковского: гироскопический момент реакции стремится совместить вектор гироскопа с направлением переносной угловой скорости по кратчайшему пути.

Следовательно, можно сформулировать следующий вывод

При действии на гироскоп с кинетическим моментом внешнего момента , вектор которого не совпадает по направлению с вектором , возникают два гироскопических момента:

первый – вызывает вынужденную прецессию (при наличии необходимой степени свободы) с угловой скоростью: в направлении совмещения по кратчайшему пути вектора с вектором ;

второй  уравновешивает внешний момент .

Порядок формирования гироскопических моментов

Последовательность формирования этих гироскопических моментов демонстрируется на рис. 6, где приняты следующие обозначения:

 система координат соответствует исходному (нулевому) положению осей карданова подвеса;

 система координат соответствует текущему положению осей карданова подвеса;

  угол поворота вокруг оси  ;

  угол поворота вокруг оси  ;

  момент гироскопический реакции, направленный вдоль оси , возникающий при действии на гироскоп переносной угловой скорости (вызывает перемещение с угловой скоростью вынужденной прецессии );

  момент гироскопический реакции вдоль оси при действии на гироскоп вынужденной прецессии с угловой скоростью ;

  момент инерции подвижных частей (полезная нагрузка при использовании гироскопа в качестве гироскопического привода) относительно оси ;

  момент инерции подвижных частей (полезная нагрузка) относительно оси ;

  инерционный момент, характеризующий динамику разгона при повороте вокруг оси ;

  инерционный момент, характеризующий динамику разгона при повороте вокруг оси ;

  управляющий момент;

  возмущающий момент.

Действие внешнего момента вдоль оси (в экваториальной плоскости ) по второму закону Ньютона вызывает появление угловой скорости нагрузки с моментом инерции , являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент (лежит в экваториальной плоскости, но ортогонален по отношению к моменту, его вызвавшему), направленный таким образом, чтобы по кратчайшему пути совместить вектор с вектором .

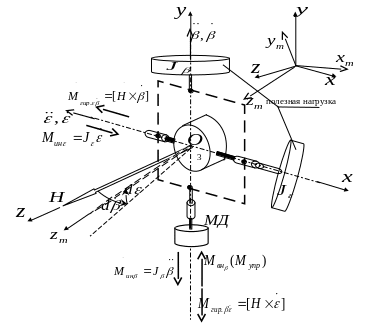
Рис. 6

Действие внешнего момента вдоль оси по второму закону Ньютона вызывает появление угловой скорости нагрузки с моментом инерции , являющейся переносной скоростью для гироскопа. По правилу гироскопической реакции возникает гироскопический момент , направленный таким образом, чтобы по кратчайшему пути совместить вектор с вектором . Гироскопический момент уравновешивает внешний момент , и движение останавливается.

Причинно-следственная последовательность физических явлений по рис. 7 выглядит следующим образом:

Даже очень небольшой момент управления , создаваемый моментным двигателем , вызывает появление значительного движущего момента относительно ортогональной оси, превышающего управляющий момент на несколько порядков. Таким образом, гироскоп может выполнять функции усилителя момента и использоваться в качестве силового гиропривода.

Запишем уравнения моментов относительно осей и :

;

.

В развернутом виде уравнения принимают вид:

(5)

;

.

Структурная схема, соответствующая системе уравнений (5) показана на рис. 7

Так как момент управления является небольшой величиной, его можно было бы использовать в качестве гироприводов относительно двух осей и . Но подсистемы плоскостей слежения оказываются связанными, как это показано на структуре по рис. 7.

Рис. 7