Колесовой Ольги 5э4 Часть 1
1.1Оценивание степени влияния фактора х на выходной показатель y.
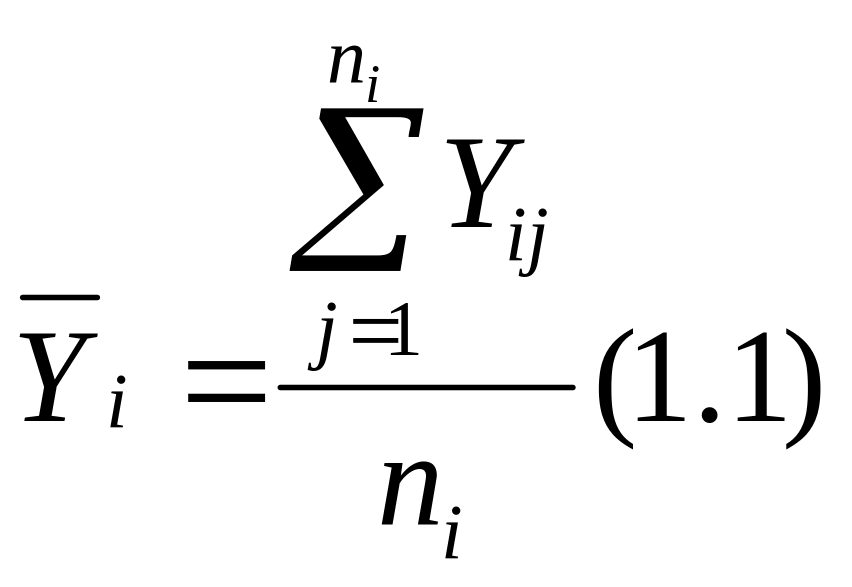
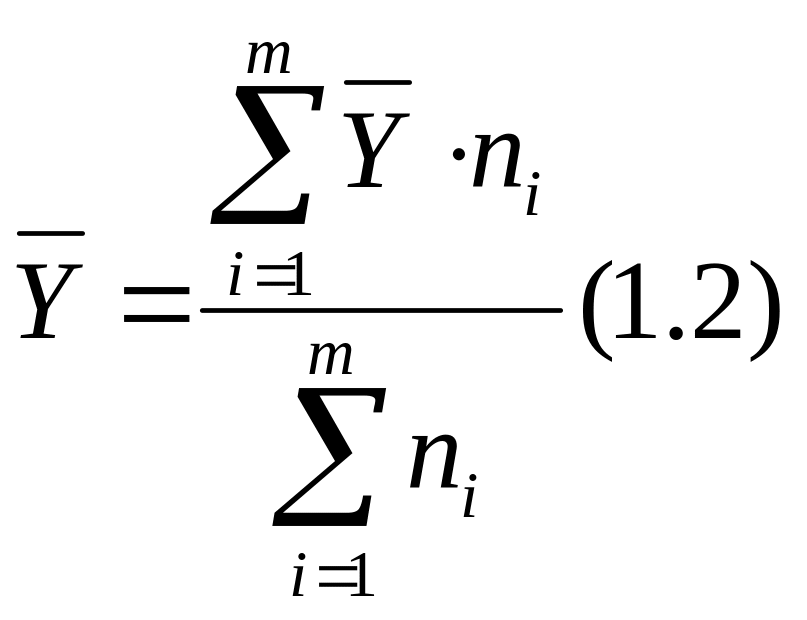
Для показателя Х7 удельный вес в ОС запасов товарно-материальных ценностей, %
Разделяем на группы, определив n=5
Максимальное значение – 65,0. Минимальное значение – 61,1
(65,0 – 61,6):5=0,68
Распределяем на группы с интервалам равным 0,68
Рассчитаем по формуле (1.1) групповые средние и подставим в графу 5
Рассчитаем общую среднюю по формуле (1.2)
Таблица 1.1 - Расчёты отбора факторов, влияющих на выходной показатель Х7 доля промышленности в валовом общественном продукте, %
Номер группы |
Значения пределов групп по фактору Х6 |
Число элементов в группе (частота) |
Значения показателя Y, соответствующие элементам группы |
Групповые средние Yi |
1 |
2 |
3 |
4 |
5 |
1 |
61,1- 62,28 |
2 |
0,244 0,238 |
0,36 |
2 |
62,29 – 62,94 |
0 |
|
|
3 |
62,97 – 63,64 |
8 |
0,314 0,318 0,320 0,313 0,305 0,274 0,263 0,255 |
0,30 |
4 |
63,65 – 64,32 |
5 |
0,337 0,302 0,286 0,280 0,270 |
0,30 |
5 |
64,33 – 65,00 |
5 |
0,326 0,318 0,300 0,290 0,250 |
0,30 |
Всего |
|
20 |
|
0,30 |
Рассчитаем межгрупповую вариацию (дисперсию). Расчёт представлен в таблице 1.2
Таблица 1.2 – Расчёт межгрупповой вариации (дисперсии)
Групповые средние Yi |
Yi-Y |
(Yi-Y)2 |
(Yi-Y)2 * ni |
0,36 |
0,07 |
0,0049 |
0,0098 |
0 |
0 |
0 |
0 |
0,30 |
0,01 |
0,0001 |
0,0008 |
0,30 |
0,01 |
0,0001 |
0,0005 |
0,30 |
0,01 |
0,0001 |
0,0005 |
Всего |
|
|
0,0116 |
Q1=0,0116
Q2=0,04087
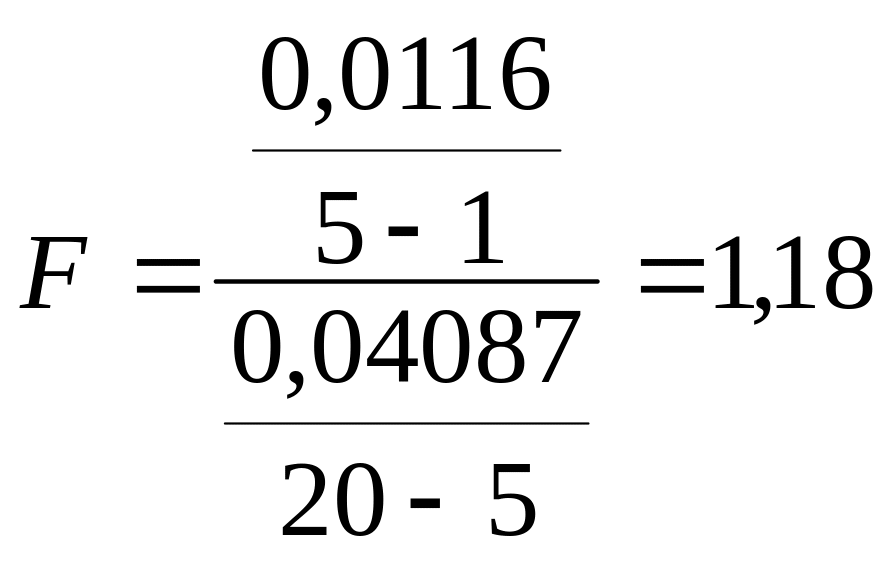
5% предел К1=5-1=4 К2-20-5=15 F=3.06
1% предел F=4.89
Сравнивая расчётное и табличные значения видим, что F-расчётное превышает табличные. Значит, влияние коэффициентов роста на удельный вес в ОС запасов товарно-материальных ценностей –существенно.
2.Для показателя Х8 уровень образования населения, занятого в народном хозяйстве, %
Аналогично п.1 рассчитаем все те же показатели для Х8
Максимальное значение – 86.8. Минимальное значение – 52.2
(86.8-52.2):5=6.92
Распределяем на группы с интервалам равным 6.92
Общая средняя
Таблица 1.3 - Расчёты отбора факторов, влияющих на выходной показатель Х8 уровень образования населения, занятого в народном хозяйстве, %
Номер группы |
Значения пределов групп по фактору Х8 |
Число элементов в группе (частота) |
Значения показателя Y, соответствующие элементам группы |
Групповые средние Yi |
1 |
2 |
3 |
4 |
5 |
1 |
52,20-59,12 |
4 |
0,314 0,318 0,337 0,326 |
0,32 |
2 |
59,13-66,05 |
2 |
0,318 0,320 |
0,31 |
3 |
66,06-72,98 |
3 |
0,313 0,302 0,305 |
0,30 |
4 |
72,99-79,91 |
5 |
0,300 0,290 0,286 0,280 0,274 |
0,28 |
5 |
79,92-86,84 |
6 |
0,270 0,263 0,255 0,250 0,244 0,238 |
0,25 |
Всего |
|
20 |
|
1,46 |
Таблица 1.4 – Расчёт межгрупповой вариации (дисперсии)
Групповые средние Yi |
Yi-Y |
(Yi-Y)2 |
(Yi-Y)2 * ni |
0,32 |
0,03 |
0,0009 |
0,0036 |
0,31 |
0,002 |
0,000004 |
0,000008 |
0,30 |
0,001 |
0,000001 |
0,000003 |
0,28 |
-0,001 |
0,000001 |
0,000005 |
0,25 |
-0,004 |
0,0016 |
0,0096 |
Всего |
|
|
0,013216 |
Q1=0,013216
Q2=0,001913
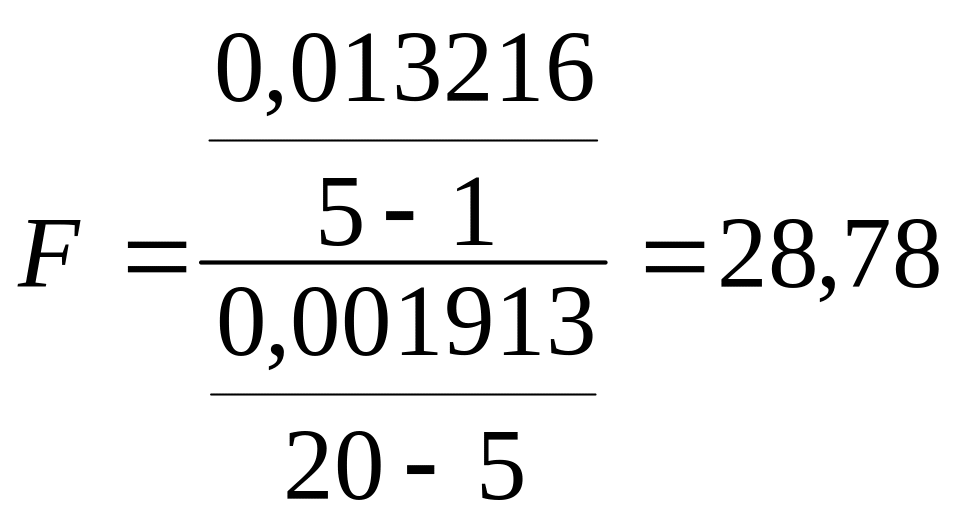
Получаем, что влияние коэффициентов роста на уровень образования населения,занятого в народном хозяйстве существенно
3. Х9 темпы роста рабочих и служащих, %
Аналогично п.1 и п.2 рассчитаем показатели для Х9
Максимальное значение – 105. Минимальное значение – 100,7
(105-100,7):5=0,9
Распределяем на группы с интервалам равным 0,9
Общая средняя
Таблица 1.5 - Расчёты отбора факторов, влияющих на выходной показатель Х9 темпы роста рабочих и служащих, %
Номер группы |
Значения пределов групп по фактору Х9 |
Число элементов в группе (частота) |
Значения показателя Y, соответствующие элементам группы |
Групповые средние Yi |
1 |
2 |
3 |
4 |
5 |
1 |
100,7 – 101,56 |
4 |
0,255 0,250 0,244 0,238 |
0,25 |
2 |
101,57 – 102,42 |
8 |
0,305 0,300 0,290 0,286 0,280 0,274 0,270 0,263 |
0,28 |
3 |
102,43 – 103,28 |
4 |
0,337 0,320 0,313 0,302 |
0,32 |
4 |
103,29 – 104,14 |
3 |
0,318 0,326 0,318 |
0,32 |
5 |
104,15 - 105 |
1 |
0,314 |
0,31 |
Всего |
|
20 |
|
1,48 |
Таблица 1.6 – Расчёт межгрупповой вариации (дисперсии)
Групповые средние Yi |
Yi-Y |
(Yi-Y)2 |
(Yi-Y)2 * ni |
0,25 |
-0,04 |
0,0016 |
0,064 |
0,28 |
-0,01 |
0,0001 |
0,0008 |
0,32 |
0,03 |
0,0009 |
0,0036 |
0,32 |
0,03 |
0,0009 |
0,0027 |
0,31 |
0,02 |
0,0004 |
0,0004 |
Всего |
|
|
0,0715 |
Q1=0,0715
Q2=0,005076
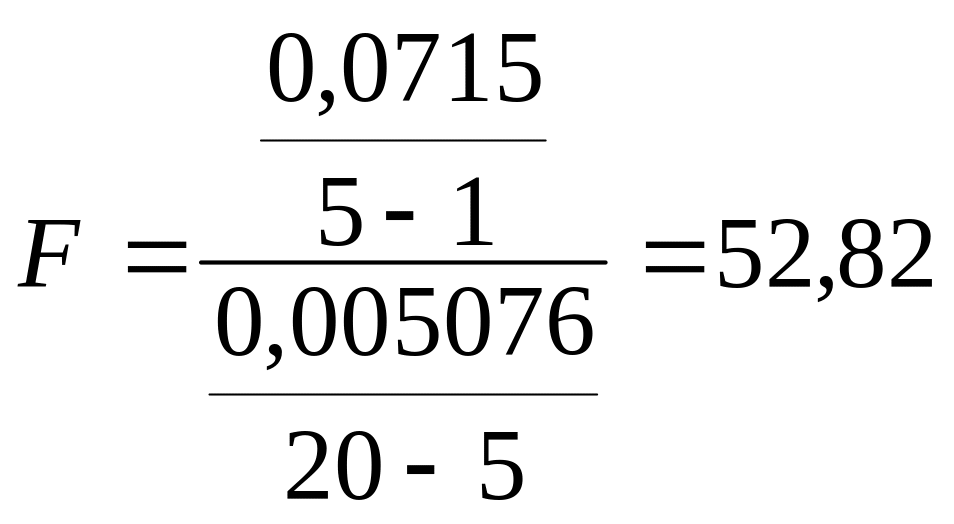
Получаем, что влияние коэффициентов роста на темпы роста рабочих и служащих существенно.
4. Получили что, F7=1,18, F8=28,78, F9=52,82 – все существенны. Но т.к. F8 из всех менее существенен, то для дальнейших расчётов будем использовать Х8 и Х9.