Математическая статистика

15. Объем дневной выручки в пяти торговых точках (в тыс. у.е.) составил: (10+β), (15+β), (20+β), (17+β), х₅. Учитывая, что 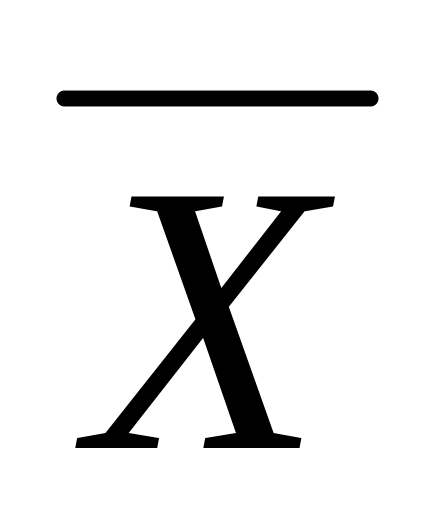= (16+β), найти выборочную дисперсию s².

16. Администрацию универсама интересует оптимальный уровень запасов продуктов в торговом зале, а также среднемесячный объем продаж товаров, не являющихся предметом ежедневного потребления в семье (таких, например, как сода). Для выяснения этого вопроса менеджер универсама в течение месяца регистрировал продажи соды и представил результаты в виде дискретного вариационного ряда

xi	x1	x2	x3	x4	x5	x6	x7
mi	2	3	8+α+β	9-α-β	5	2	1

где x₁=α, x_i=x₁+(i-1), , m_i – частоты.

Требуется:

а) построить полигон относительных частот ;

б) вычислить среднее выборочное , выборочную дисперсию D_x и среднее выборочное квадратичное отклонение σ_x.

Какие рекомендации следует дать администрации универсама?

17. При изучении структуры коммерческих банков по объявленному уставному фонду из трех тысяч банков страны было отобрано по схеме собственно случайной бесповторной выборки сто. Данные о распределении банков по этому признаку представлены в таблице:

Размер уставного фонда	xmin	До 10+10β	10+10β	20+20β	30+30β	40+40β	Свыше 50+50β	Итого
	xmax		20+20β	30+30β	40+40β	50+50β
Число банков	ni	7	9	18	34	22	10	100

Найти:

а) вероятность того, что средний размер уставного фонда всех коммерческих банков отличается от среднего размера его в выборке не более чем на пять миллионов рубле й (по абсолютной величине);

б) границы, в которых с вероятностью 0,9 заключена доля всех банков, размер уставного фонда которых не менее (40+40β) миллионов рублей;

в) объем бесповторной выборки, при котором то же отклонение среднего размера уставного фонда всех банков (не более пяти миллионов рублей см. пункт а)), можно гарантировать с вероятностью 0,95.

18. По данным задания 14 необходимо:

а) выдвинуть гипотезу о виде модели, аппроксимирующей эмпирическое распределение, обосновав выбор;

б) используя χ² - критерий Пирсона, при уровне значимости =0,05 проверить гипотезу о том, что случайная величина Х – размер уставного фонда распределена по нормальному закону.

Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.

19. В процессе исследования среднедушевого дохода (в руб.) обследовано 100 семей. Выявлены оценки: = (1500+100β), s = (200+10β). В предположении о нормальном законе:

а) найти долю семей, чей среднедушевой доход находится в пределах от 1200 до 1800;

б) выяснить при уровне значимости =0,05 можно ли считать (1600+100β) руб. нормативом среднедушевого дохода (проверить гипотезу H₀: а= (1600+100β) против конкурирующей гипотезы Н₁: а≠ (1600+100β);

в) построить доверительный интервал для оценки неизвестного математического ожидания а и дисперсии σ² (принять γ = 0,95).

20. По данным 16 сотрудников фирмы, где работает (200+10β) человек, среднемесячная заработная плата составила (300+10β) у.е., при s = (70+β) у.е. Какая минимальная сумма должна быть на счету фирмы, чтобы с вероятностью 0,99 гарантировать выдачу заработной платы всем сотрудникам?

21. С целью размещения рекламы опрошено (400+10β) телезрителей, из которых данную передачу смотрят (150+10β) человек. С доверительной вероятностью 0,95 найти долю телезрителей, охваченных рекламой в лучшем случае. Случайны ли результаты опроса, если согласно статистике доля телезрителей, охваченных рекламой составляет (0,41+β/100) при уровне значимости =0,05?

22. Распределение пятидесяти предприятий по размерам основных производственных фондов Х (миллионов рублей) и выпуску продукции У (миллионов рублей) дано в таблице:

	y1	y2	y3	y4	y5	mxi
x1	2	3	–	–	–	5
x2	3	8	2	–	–	13
x3	–	8+α	12+β	–	–	20+α+β
x4	–	–	16-α	14­-β	­–	30-α-β
x5	–	–	9	10	–	19
x6	–	–	3	6	1	10
x7	–	–	–	1	2	3
myj	5	19+α	42+β-α	31­-β	3	n=100

x₁=10-α, x_i=x₁+(i-1)h_x, h_x=1-0,1(10-β)^, y_j=y₁+(j-1)h_y, h_y=10-α, , .

Необходимо:

а) вычислить групповые средние и построить эмпирические линии регрессии;

б) предполагая, что между переменными Х и У существует линейная корреляционная зависимость:

- найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию получившихся уравнений;

- вычислить коэффициент корреляции, на уровне значимости =0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и У;

- в случае отклонения гипотезы об отсутствии корреляционной зависимости объема выпуска продукции от размера основных производственных фондов оценить меру влияния размера основных производственных фондов на объем выпуска продукции (использовать коэффициент детерминации и корреляционное отношение);

-используя соответствующее уравнение регрессии, оценить средний выпуск продукции предприятий, основные фонды которых составляют 81 млн руб..

23. Сформулировать две задачи из предметной области своей будущей профессиональной деятельности, требующие применения вероятностно-статистических методов. Привести необходимые исходные данные, решить задачи, сделать обоснованные выводы.