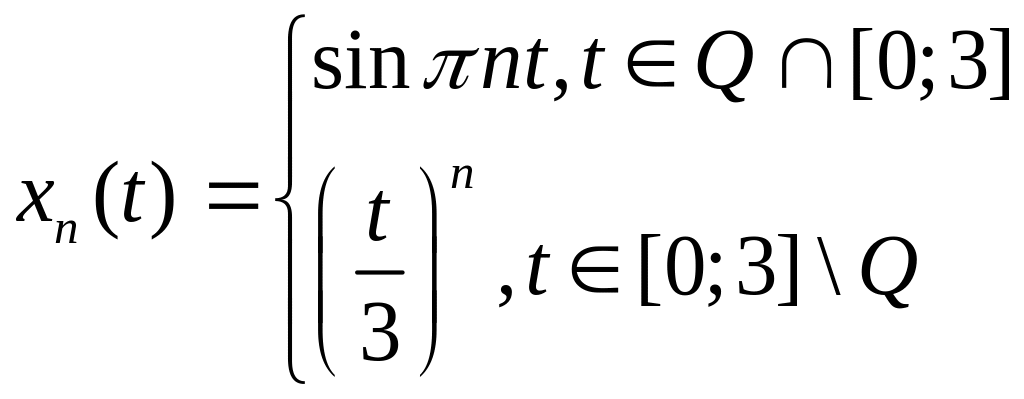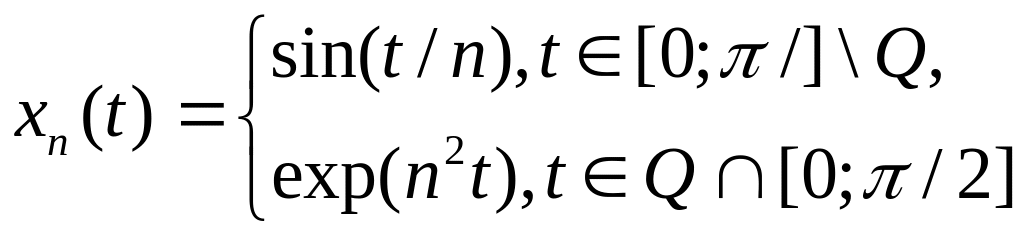Содержание

Введение…………………………………………………………………..4

1 Метрические пространства…………………………………………….5

Тема 1 Сходящиеся последовательности в метрических

пространствах…………………………………………………………….5

Тема 2 Топология метрических пространств……………………… 13

Тема 3 Полнота метрических пространств…………………… ……19

Тема 4 Непрерывные отображения………………………………….25

Тема 5 Компактные множества в метрических пространствах……31

Тема 6 Сжимающие отображения…………………………………...35

2 Линейные нормированные пространства и операторы в них……...41

Тема 1 Линейные нормированные пространства…………………..41

Тема 2 Линейные ограниченные операторы в банаховых

пространствах………………………………………………………...…48

Тема 3 Обратные операторы…………………………………………57

Литература……………………………………………………………….63

Введение

Функциональный анализ является одним из важнейших разделов математического анализа, воплотившим в себе единство абстрактной и прикладной математики.

Данный сборник содержит задачи, подобранные в соответствии с программой курса «Функциональный анализ и интегральные уравнения» для студентов специальности 1-31 03 01-02 − «Математика (научно-педагогическая деятельность)» (5-й семестр обучения). В сборнике представлены наиболее типичные задачи по разделам «Метрические пространства», «Линейные нормированные пространства и операторы в них».

Предлагаемый материал направлен на закрепление теоретического материала путем самостоятельного решения задач, а также на овладение основными приемами и методами решения задач по функциональному анализу.

Сборник предназначен, в первую очередь, для проведения лабораторных и практических занятий по курсу «Функциональный анализ и интегральные уравнения». Подбор задач осуществлен в соответствии с расположением учебного материала в программе дисциплины. Задачи объединены в группы по темам, по каждой из которых учебным планом по дисциплине «Функциональный анализ и интегральные уравнения» для студентов специальности 1-31 03 01-02 − «Математика (научно-педагогическая деятельность)» предусмотрено выполнение лабораторной работы. Для каждого типового задания подобрано 6 вариантов задач примерно одинаковой сложности. Это позволит также использовать сборник для самоконтроля при подготовке к экзамену. Самостоятельное решение задач по функциональному анализу часто вызывает большие трудности у студентов, поэтому пособие содержит примеры решения типовых задач.

1 Метрические пространства

Тема 1

Сходящиеся последовательности в метрических пространствах

1.1.1 Проверить, сходится ли заданная последовательность x_n точек метрического пространства X к точке a, если выполнены следующие условия (таблица 1.1.1).

Таблица 1.1.1

вариант
1
2
3
4
5
6

1.1.2 Проверить, сходится ли заданная последовательность x_n точек метрического пространства X к точке a, если выполнены следующие условия (таблица 1.1.2).

Таблица 1.1.2

вариант
1	2		4
1
2
3

Окончание таблицы 1.1.2

1	2		4
4
5
6

1.1.3 Проверить, сходится ли заданная последовательность x_n точек метрического пространства X к точке a, если выполнены следующие условия (таблица 1.1.3).

Таблица 1.1.3

вариант	X
1
2
3
4
5
6

1.1.4 Является ли данное условие: а) необходимым, б) достаточным, в) необходимым и достаточным для сходимости последовательности x_n в метрическом пространстве X (таблица 1.1.4)?

Таблица 1.1.4

вариант	X	Условие
1	2	3
1		существует предел числовой последовательности
2		существует предел числовой последовательности
3		, где
4		существует предел числовой последовательности

Окончание таблицы 1.1.4

1	2	3
5		, где
6		, где

1.1.5 Найти предел последовательности x_n в метрическом пространстве X, если он существует (таблица 1.1.5).

Таблица 1.1.5

вариант	X
1
2
3
4
5
6

Примеры решения типовых задач

1 Проверить, сходится ли заданная последовательность x_n точек метрического пространства X к точке a.

Пример 1 .

Решение Рассмотрим расстояние | |. Так как при всех имеем

– 0

при , то . Значит, x_n сходится к a в .

Пример 2 .

Решение Рассмотрим . Обозначим через и найдем наибольшее значение функции на отрезке . Имеем , , если или .

, ,

.

Значит, (по правилу нахождения наибольшего значения функции на отрезке), ,

а поэтому x_n сходится к a в .

Пример 3 x_n = .

Решение

при n .

Так как не стремится к нулю, то x_n не сходится к a в l₃.

Пример 4 x_n = , , .

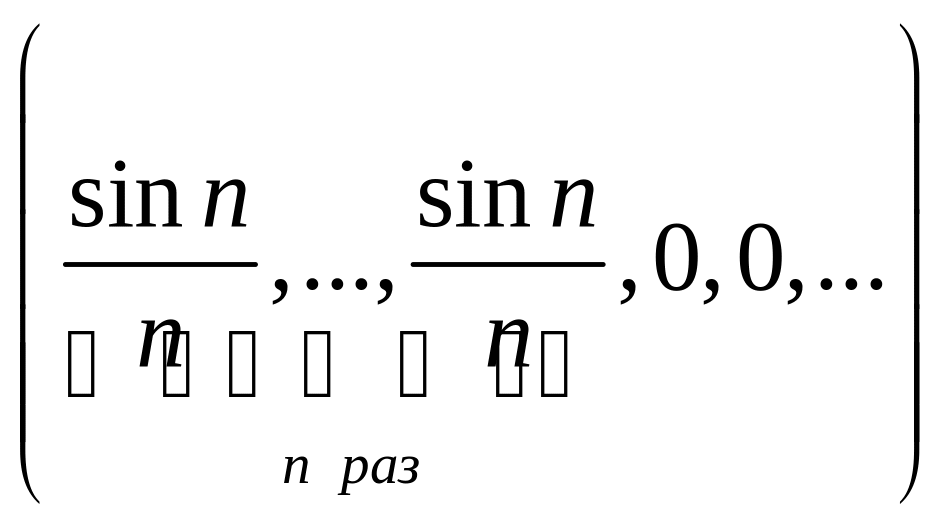Решение

при n .

Значит, x_n сходится к a в l₂.

Пример 5 .

Решение

.

Применим теорему Беппо Леви о предельном переходе под знаком интеграла. Обозначим . Функция является интегрируемой на для любого , и . Кроме того, . Значит, по теореме Б. Леви,

.

Следовательно, x_n сходится к a в .

Пример 6 , , .

Решение

при (мы воспользовались тем, что при ). Значит, x_n сходится к a в .

2 Является ли данное условие: а) необходимым, б) достаточным,

в) необходимым и достаточным для сходимости последовательности x_n в метрическом пространстве X?

Пример 1 – пространство непрерывных функций с метрикой .

Условие: последовательность x_n(t) поточечно сходится к непрерывной функции a(t).

Решение Не нарушая общности, можем считать, что . Покажем, что условие не является ни необходимым, ни достаточным. Для выяснения достаточности условия рассмотрим следующую последовательность x_n(t), заданную на графически (рисунок 1):

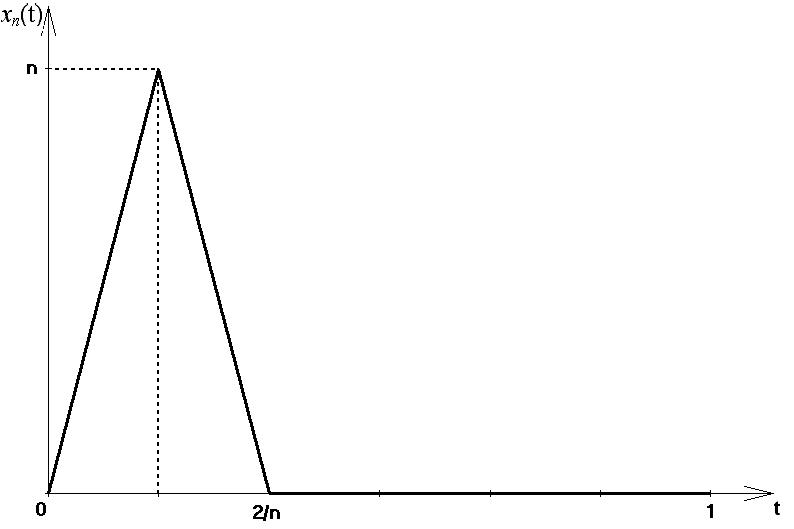
Рисунок 1 – График функции x_n(t)

Последовательность x_n сходится к поточечно на (почему?), но

1,

то есть не стремится к нулю. Значит, данное условие не является достаточным для сходимости последовательности x_n в метрическом пространстве .

Теперь допустим, что в , то есть 0 при . Покажем на примере, что отсюда не следует поточечная сходимость x_n к a. Рассмотрим последовательность и функцию . Имеем

0 при .

Значит, в . Но не сходится к поточечно, так как при . Значит, данное условие не является необходимым для сходимости последовательности x_n в метрическом пространстве .

Пример 2 .

Условие: , где .

Решение Положим . Тогда данное условие означает, что при . Докажем, что это условие является достаточным для сходимости последовательности x_n к а в пространстве .

Поскольку при выполнении этого условия 1 при достаточно больших n, то при этих n и при всех k имеем . Поэтому при этих n и при всех k. Значит,

,

а это значит, что 0. Следовательно, x_n a в . Достаточность доказана.

Теперь покажем, что условие не является необходимым. Рассмотрим последовательность и точку

из . Имеем 0 ( ) как остаток сходящегося ряда. Значит, x_n a в . Но в этом примере (сравните с гармоническим рядом), а потому данное условие не выполняется.

3 Найти предел последовательности x_n в метрическом пространстве X, если он существует.

Пример 1 .

Решение

1 способ Допустим, x_n сходится к некоторому a в . Так как для любого k справедливо неравенство

,

то имеем и покоординатную сходимость x_n к a. Но покоординатно x_n «сходится» к последовательности

,

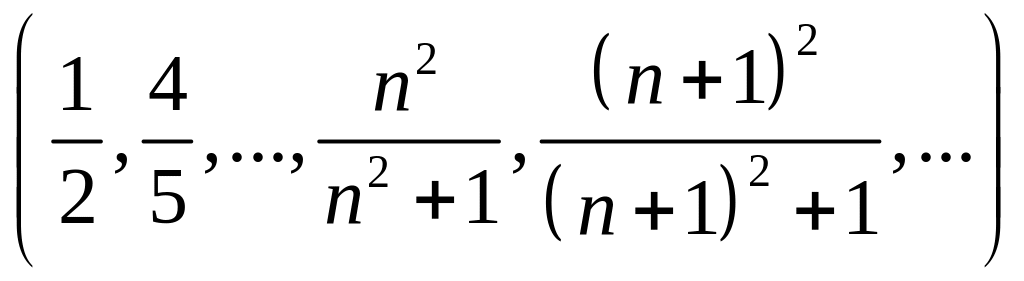которая не принадлежит пространству (ряд расходится, по необходимому признаку). Мы пришли к противоречию. Значит, x_n не сходится в .

2 способ Так как при , последовательность x_n не является фундаментальной. Следовательно, x_n не сходится в .

Пример 2 X x_n= .

Решение

1 способ Допустим, x_n сходится к некоторому a в . Так как при для любого k, то имеем покоординатную сходимость x_n к a. Но покоординатно x_n «сходится» к последовательности

,

для которой 1 (почему?) при . Следовательно, x_n не сходится к a в . Противоречие.

2 способ Заметим, что последовательность x_n не является фундаментальной в . Действительно, x_n+1 = ,

1 при . Так как x_n не фундаментальна в , то она не сходится в .

Тема 2

Топология метрических пространств

1.2.1 Является ли данное множество М открытым, замкнутым, ограниченным в пространстве ? Найти его замыкание, внутренние и граничные точки (таблица 1.2.1).

Таблица 1.2.1

вариант	М	вариант	М
1		4
2		5
3		6

1.2.2 Для данного множества А выяснить, является ли множество открытым, замкнутым, ограниченным в (таблица 1.2.2).

Таблица 1.2.2

вариант		А	вариант		А
1	1		4
2	2		5	3/2
3	2		6	2	{ }

Примеры решения типовых задач

1 Является ли данное множество открытым, замкнутым, ограниченным в пространстве ? Найти его замыкание, внутренние и граничные точки.

Пример 1 .

Решение Множество не является открытым, и более того, ни одна его точка не является внутренней. Действительно, и для любого шара имеем , но , так как .

Множество является замкнутым, так как оно содержит в себе пределы всех своих сходящихся последовательностей. Действительно, если в , , то и . А это значит, что .

Граница множества совпадает с самим множеством , что теперь сразу следует из формулы .

Множество не является ограниченным, так как последовательность , но .

Пример 2 .

Решение Покажем, что является открытым. Возьмём , то есть

.

Тогда . Покажем, что шар . Возьмём . Это значит, что . Тогда

.

Значит, .

Так как открыто, то .

Множество не является замкнутым, так как содержит не все свои предельные точки. Действительно, возьмём последовательность

из . Тогда , но , т.е. .

Замечание Нормированное пространство X всегда связно, так как любые две его точки х и у можно связать непрерывным путем

, лежащим в X, а потому в нем нет открытых и одновременно замкнутых собственных подмножеств.

Замыкание . Действительно, если принадлежит , то найдется последовательность равномерно сходящаяся к на . А тогда

.

Обратно, если , то последовательность принадлежит и сходится к равномерно (проверьте!), а потому принадлежит .

Теперь ясно, что граница .

Наконец, не является ограниченным, так как , но .

Пример 3 .

Решение Покажем, что открыто. Возьмём . Тогда , а потому . Рассмотрим . Для любого имеем , а тогда

.

Покажем, что замыкание множества есть . Действительно, если принадлежит , то найдется последовательность , равномерно сходящаяся к на . А тогда .

Обратно, если , то последовательность принадлежит и сходится к равномерно на (проверьте), а потому принадлежит .

Теперь ясно, что граница .

Очевидно, что данное множество ограничено.

2 Для данного множества А выяснить, является ли множество открытым, замкнутым, ограниченным в .

Пример 1 .

Решение Множество замкнуто, так как содержит в себе все свои предельные точки. Действительно, если то (почему?). Но так как , то и . Значит, .

Так как замкнуто, то оно не является открытым, поскольку пространство связно (см. замечание к примеру 2 в задаче 1). Но легко дать и прямое доказательство. Действительно, точка принадлежит , но для любого точка , хотя и лежит в − окрестности точки .

Наконец, ограничено, так как

.

Пример 2 .

Решение Множество не является открытым. Для доказательства покажем, что точка не является для него внутренней. Возьмём и найдём такое натуральное N, что Тогда , но , поскольку .

Множество не замкнуто. Действительно, рассмотрим . Тогда сходится к точке , так как при , но .

Множество ограничено, так как .

Пример 3 .

Решение Покажем, что множество открыто.

Возьмём . Найдется такое , что . Если (шар рассматривается, конечно, в ), то . Тогда и . Теперь, в силу неравенства Минковского, имеем

.

Значит, , т. е. . Итак, .

Так как открыто, то не замкнуто по замечанию из решения примера 2 к задаче 1. Дадим прямое доказательство этого факта. Точки где , очевидно, принадлежат . Но в то же время сходится в к .

Покажем, что не ограничено. Рассмотрим последовательность

.

Имеем: , так как

,

но в то же время при .

Пример 4 .

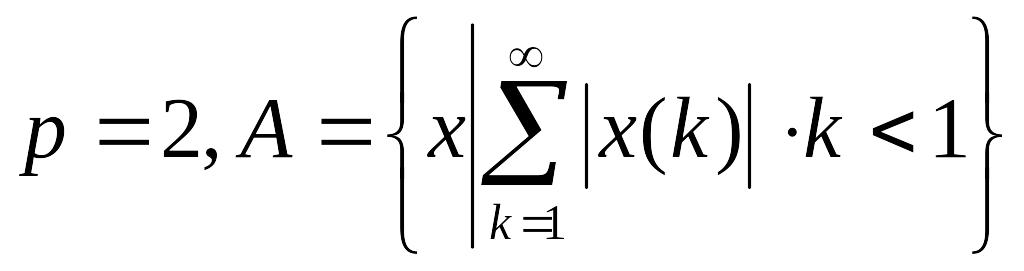Решение Покажем, что не является открытым. Возьмём и . Найдётся такое натуральное , что . Тогда , но .

Множество не является и замкнутым. Для доказательства рассмотрим последовательность . Она сходится к точке , которая не принадлежит , так как .

Множество ограничено, поскольку неравенство влечет

.

Тема 3

Полнота метрических пространств

1.3.1 Является ли последовательность фундаментальной в данном пространстве X? Найти , если он существует (таблица 1.3.1).

Таблица 1.3.1

вариант	X
1
2
3
4
5
6

1.3.2 Выяснить, является ли заданное пространство полным.

Вариант 1 а) пространство непрерывно дифференцируемых на отрезке функций с метрикой

;

б) пространство всех дважды дифференцируемых на отрезке функций с метрикой .

Вариант 2 а) пространство числовых последовательностей , удовлетворяющих условию , с метрикой ;

б) пространство всех непрерывных на отрезке функций с метрикой .

Вариант 3 а) пространство всех ограниченных числовых последовательностей с метрикой ;

б) с метрикой .

Вариант 4 а) пространство сходящихся к нулю последовательностей с метрикой ;

б) с метрикой .

Вариант 5 а) Пространство с сходящихся последовательностей с метрикой ;

б) с метрикой .

Вариант 6 а) Пространство ограниченных и непрерывных на интервале функций с метрикой ;

б) с метрикой .

Примеры решения типовых задач

1 Является ли последовательность фундаментальной в данном пространстве X? Найти , если он существует.

Пример 1 ,

, где K – канторово множество.

Решение Так как канторово множество имеет лебегову меру нуль, то и − множество меры нуль. Значит, почти всюду.

Покажем, что сходится к 0 в . Для этого рассмотрим

и воспользуемся разложением по формуле Тейлора:

при .

Получаем:

при .

Тот же результат мы получим, применив теорему Лебега о предельном переходе под знаком интеграла.

Итак, сходится к 0, а потому она фундаментальна.

Пример 2 .

Решение Так как − множество меры нуль, то почти всюду на . Покажем, что эта последовательность не фундаментальна в нашем пространстве:

.

(мы воспользовались леммой Римана из теории рядов Фурье, согласно которой , но можно было бы вычислить интеграл и непосредственно).

2 Является ли метрическое пространство полным?

Пример 1 ­ − пространство вещественнозначных ограниченных функций на , наделенное метрикой .

Решение Покажем, что любая фундаментальная последовательность ( ) в является сходящейся. Ее фундаментальность означает, что : выполняется неравенство

. (1)

Зафиксируем произвольное число . Тогда числовая последовательность ( ), в силу (1), является фундаментальной в . По причине полноты пространства , последовательность сходится. Положим , t . Тем самым на определена функция , к которой сходится поточечно. Осталось доказать, что

1) ;

2) при .

С этой целью перейдем в (1) (а точнее, в неравенстве , справедливом при всех t из ) к пределу при . Получим, что

. (2)

В частности, при +1 выполняется оценка:

,

из которой следует ограниченность . Следовательно, . Наконец, формула (2) означает, что . Поэтому

при .

Пример 2 ( ) – пространство числовых последовательностей , удовлетворяющих условию: , где , ­− заданная числовая последовательность; .

Решение Покажем, что данное пространство полно. Пусть ( ) − фундаментальная последовательность в . Это значит, что

: . (3)

Тогда для любого фиксированного имеем:

, или .

Следовательно, для любого фиксированного числовая последовательность является фундаментальной, а потому сходится. Обозначим и положим . Осталось показать, что

1) и

2) при .

Из (3) следует, что любого фиксированного , что в пределе при дает . Переходя теперь к пределу при , получим , т. е.

: . (4)

Возьмем какие-нибудь и и обозначим

.

Вследствие неравенства Минковского, имеем

,

а это значит, что . Теперь (4) показывает, что при , а потому ( ) сходится в нашем пространстве к .

Пример 3 − ­ множество непрерывно дифференцируемых на функций с метрикой .

Решение Рассмотрим последовательность и покажем, что она является фундаментальной, но не является сходящейся в нашем пространстве. Заметим, что эта последовательность поточечно сходится к функции , где

.

А так как , то, по теореме Лебега, при . Это означает, что в пространстве последовательность сходится к . Следовательно, она фундаментальна в Х. С другой стороны, если предположить, что последовательность сходится в данном пространстве Х к некоторой функции , то получим, что имеет два предела ( и ) в .­ Противоречие. Итак, данное пространство не является полным.

Тема 4

Непрерывные отображения

1.4.1 Выяснить, является ли заданное отображение на своей естественной области определения непрерывным в точке (таблица 1.4.1)?

Таблица 1.4.1

вариант	X	Y	F
1
2
3
4
5
6

1.4.2 Является ли заданное отображение : а) непрерывным; б) равномерно непрерывным; в) удовлетворяющим условию Липшица (таблица 1.4.2)?

Таблица 1.4.2

вариант	X	Y	F
1
2
3
4
5
6

Примеры решения типовых задач

1 Является ли заданное отображение на своей естественной области определения непрерывным в точке ?

Пример 1 , .

Решение Очевидно, что заданное отображение определено на всем . Представим его в виде , где , , и покажем, что и непрерывны в любой точке . Пусть последовательность сходится к в . Тогда

| - | .

Отсюда следует, что непрерывно.

Докажем непрерывность . Так как функция , то она ограничена на , т. е. . А так как равномерно на , то, начиная с некоторого номера, на (почему?). Тогда

.

Отсюда следует, что в . Поэтому в силу произвольности отображение непрерывно в любой точке из .

Пример 2 .

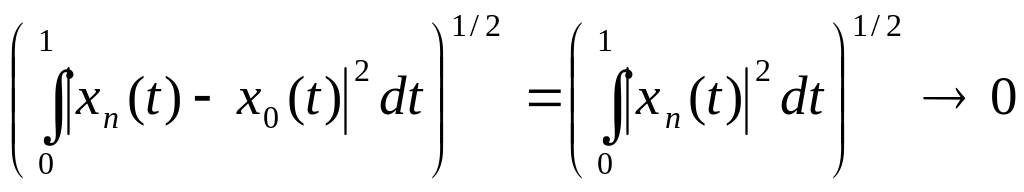Решение Пусть последовательность сходится к в . Тогда при .

Теперь в силу неравенства Коши-Буняковского,

.

(аналогичные вычисления показывают, что принадлежит при из ; поэтому отображение определено на всем ). Значит, – непрерывное отображение в точке .

Пример 3 .

Решение Покажем, что отображение не является непрерывным. Возьмём последовательность . _[0;1/n], которая стремится к нулю в . Действительно,

при .

Рассмотрим теперь выражение

= = = = .

Следовательно, последовательность не стремится к нулю при , а потому не стремится к .

Пример 4 .

Решение Покажем, что отображение не является непрерывным. Заметим, что

= .

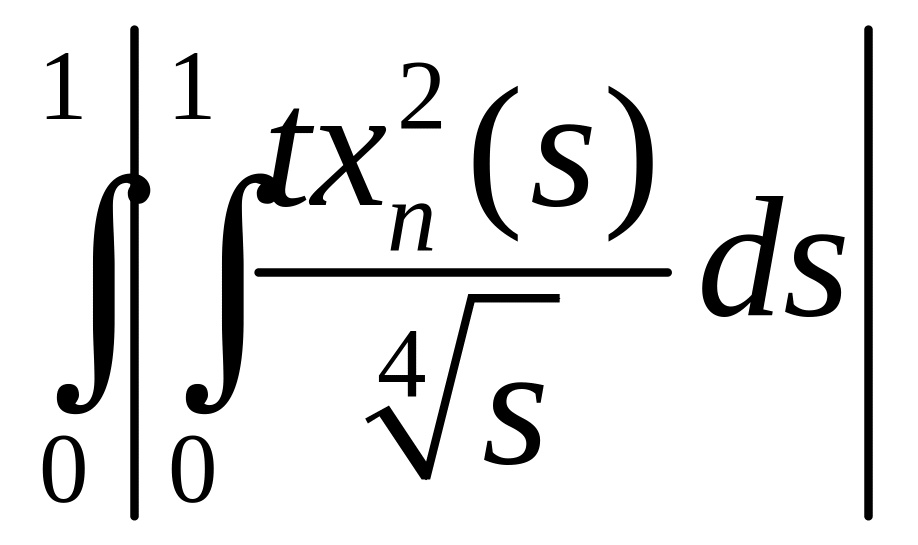
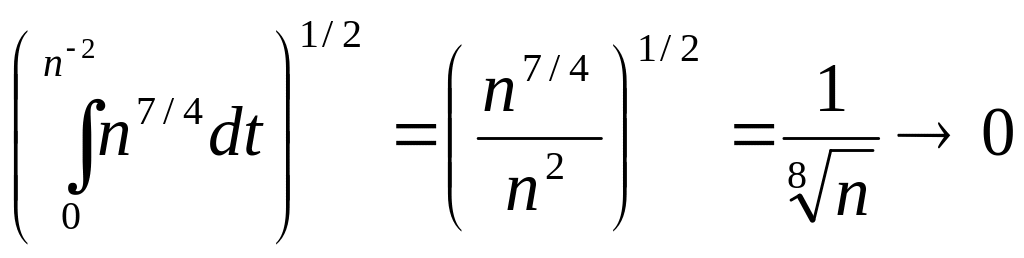Возьмем последовательность , которая сходится к нулю в , так как при .

Тогда при ,

а потому не стремится к .

2 Является ли заданное отображение : а) непрерывным;

б) равномерно непрерывным; в) удовлетворяющим условию Липшица?

Пример 1 .

Решение а) Отображение является непрерывным, так как

(мы воспользовались неравенством ; здесь ).

б) Покажем, что не является равномерно непрерывным. Возьмём

. Тогда → 0 при , но

- + ,

а значит, не стремится к нулю при . Это противоречит определению равномерной непрерывности (проверьте).

в) Так как не является равномерно непрерывным, то оно не удовлетворяет условию Липшица (почему?).

Пример 2 .

Решение Покажем, что удовлетворяет условию Липшица с константой . Заметим, что

{ }.

Рассмотрим функцию . Тогда

= .

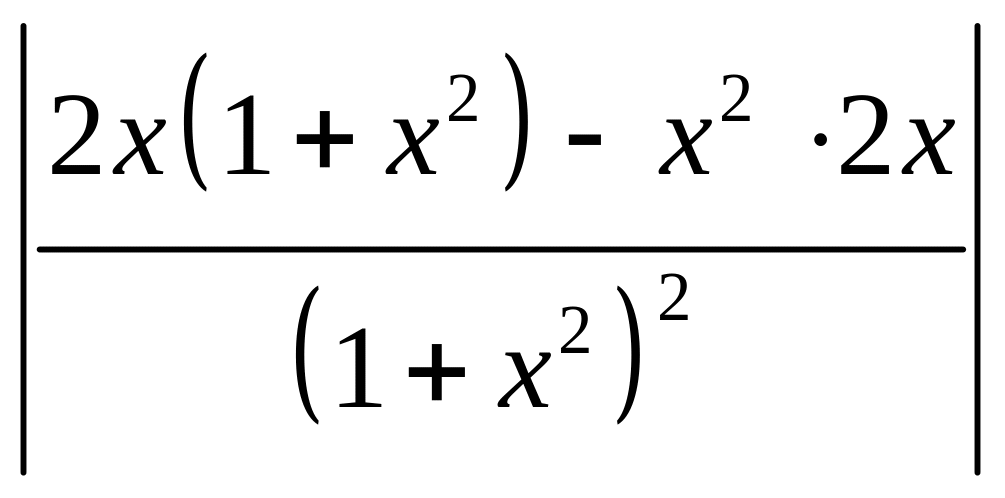Следовательно, по теореме Лагранжа, , а значит,

{ } .

Так как удовлетворяет условию Липшица, то оно равномерно непрерывно, а потому и непрерывно.

Пример 3 .

Решение Покажем, что удовлетворяет условию Липшица. Действительно,

= .

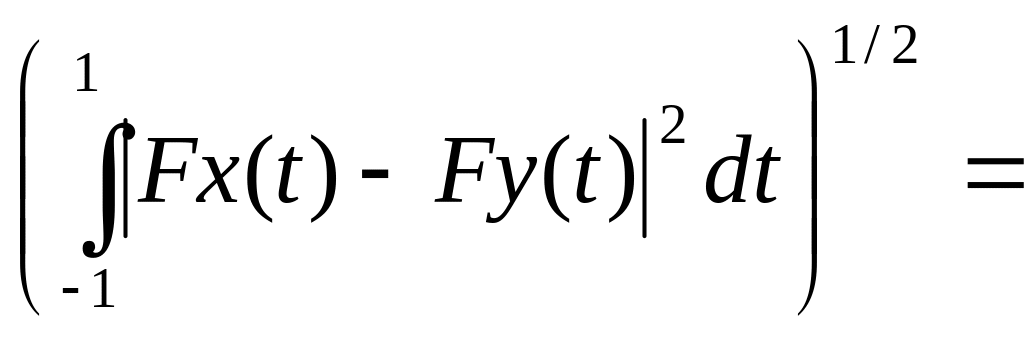
Так как , то по теореме Лагранжа . Поэтому при любых x,y

.

Так как удовлетворяет условию Липшица, то оно является равномерно непрерывным.

Пример 4 .

Решение а) Покажем, что непрерывно. Действительно, если в , то числовая последовательность сходится к . Тогда 0 при .

б) Покажем, что не является равномерно непрерывным. Пусть

, , , .

Тогда при .

Но при .

в) Так как не является равномерно непрерывным, то оно не удовлетворяет и условию Липшица.

Пример 5 .

Решение а) Покажем, что не удовлетворяет условию Липшица. Допустим противное, то есть что

.

Возьмем .

Так как

, (1)

то получим , то есть , . Противоречие.

б) Покажем, что является равномерно непрерывным.

Заметим, что функция является равномерно непрерывной на (она равномерно непрерывна на по теореме Кантора и равномерно непрерывна на , так как при ). Равномерная непрерывность функции означает, что

.

Теперь если , то , тогда, в силу равенства (1),

.

Тема 5

Компактные множества в метрических пространствах

1.5.1 Выяснить, является ли множество М предкомпактным, компактным в (таблица 1.5.1).

Таблица 1.5.1

вариант	М	вариант	М
1		4	{ ) | }
2		5	{ | }
3		6	{ | }

1.5.2 Является ли множество М предкомпактным в (таблица1.5.2)?

Таблица 1.5.2

вариант	р	М
1	2	{ }
2	1	{ }
3	2	{ }
4	2	{ }
5	1	{ }
6	1	{ }

Примеры решения типовых задач

1 Выяснить, являются ли данные множества предкомпактными, компактными в .

Пример 1 а) ;

б) .

Решение Проверим для множества М условия теоремы Арцела-Асколи.

Рассмотрим функцию . Пусть . Тогда непрерывна на и .

Множество является компактом. По теореме Вейерштрасса, ограничена на , т.е. справедливо неравенство . Значит, М − равномерно ограничено ( впрочем, легко проверить и непосредственно, что при наших условиях e).

Проверим равностепенную непрерывность множества М. По теореме Кантора, равномерно непрерывна на . Если обозначить через произвольную точку из К, то равномерная непрерывность означает, что , таких, что , и , таких, что (ρ обозначает евклидову метрику в К), справедливо неравенство

.

Отсюда следует равностепенная непрерывность множества М (см. определение). Значит, по теореме Арцела-Асколи, М − предкомпактно.

Для доказательства компактности множества М теперь достаточно проверить его замкнутость в . Но это тоже следует из непрерывности функции . В самом деле, если х − предельная точка множества М, то найдется последовательность функций из М, сходящаяся к х в . По теореме Больцано-Вейерштрасса, из последовательности точек множества К можно выбрать подпоследовательность , сходящуюся к точке . Тогда поточечно , а потому, в силу единственности предела, . Итак, М – компакт.

Далее, так как М₁ М, то множество М₁ предкомпактно. Но М₁ не является компактом, так как не замкнуто в . Действительно, функции М₁, но предел этой последовательности не принадлежит множеству М₁.

Пример 2 .

Решение

1 способ Это множество является равномерно ограниченным, но не является равностепенно непрерывным. Действительно, возьмем . Тогда найдется такое натуральное n, что точки и удовлетворяют неравенству , но в то же время . Значит, по теореме Арцела-Асколи, М не является предкомпактным, а потому и компактным множеством.

2 способ М не является предкомпактным, так как из него нельзя извлечь сходящейся в подпоследовательности. Действительно, все его подпоследовательности сходятся к разрывной функции.

Пример 3 { | }.

Решение Множество М равномерно ограничено, так как

1.

Множество М равностепенно непрерывно, так как и , таких, что , имеем

.

Значит, по теореме Арцела-Асколи, М − предкомпактно.

Покажем, что М содержит все свои предельные точки. Пусть х есть предельная точка множества М, равномерно на . В силу периодичности синуса, можно считать, что . При этом промежуток удобно отождествлять с фактор-группой , то есть с единичной окружностью, наделенной естественной топологией, в которой она компактна. (Отличие здесь в том, что если последовательность в сходится к , то в этой топологии предел считается равным 0). Заметим, что в этой топологии существует . Действительно, если допустить противное, то найдутся две подпоследовательности и , имеющие различные пределы и соответственно. Но тогда , откуда . Противоречие. Следовательно, .

Значит, М – замкнутое множество, откуда следует, что М – компакт.

Пример 4 .

Решение Множество М равномерно ограничено, так как

1.

Но множество не является равностепенно непрерывным. Действительно, возьмем . Тогда найдется такое натуральное n, что точки и удовлетворяют неравенству , но в то же время . Значит, по теореме Арцела-Асколи, М не является предкомпактным, а потому и компактным множеством.

2 Является ли множество М предкомпактным в ?

Пример 1 { }.

Решение Проверим критерий предкомпактности в .

1) Множество М является ограниченным, поскольку , а потому .

2) Так как ряд сходится, то его остаток стремится к нулю, то есть .

Поэтому .

Значит, множество М − предкомпактно.

Тема 6

Сжимающие отображения

1.6.1 Является ли отображение F метрического пространства X в себя сжимающим? Найти , где . Оценить расстояние от до неподвижной точки в случае, если F является сжимающим (таблица 1.6.1).

Таблица 1.6.1

вариант	X	F
1
2
3
4
5
6

1.6.2 Применим ли принцип сжимающих отображений к заданному интегральному уравнению в пространстве Х при ? При с точностью до 0,01 найти приближенное решение и сравнить его с точным решением (таблица 1.6.2).

Таблица 1.6.2

вариант	Х				Уравнение
1	2	3	4	5	6
1
2

Окончание таблицы 1.6.2

1	2	3	4	5	6
3
4
5
6

Примеры решения типовых задач

1 Является ли отображение F метрического пространства X в себя сжимающим? Найти , где . Оценить расстояние от до неподвижной точки, если F является сжимающим.

Пример 1 .

Решение Оценим расстояние в

(мы воспользовались неравенством ). Значит, F является сжимающим отображением с константой Липшица .

Построим последовательность . По условию поэтому .

А так как , где – неподвижная точка, то

Пример 2 .

Решение Оценим расстояние в .

.

Значит, – сжимающее отображение с константой .

По условию, . Тогда а потому

(на самом деле, как легко проверить, является неподвижной точкой).

Пример 3 .

Решение Допустим, что отображение F является сжимающим, то есть .

При из этого неравенства следует, что

. (1)

Подставив в левую часть неравенства (1), получим

при

(мы воспользовались эквивалентностью при ).

Правая же часть неравенства (1), как легко проверить, при этом значении х равна . Следовательно, неравенство (1) при указанных x,y и примет вид: ­ противоречие. Значит, F не является сжимающим. (Аналогичное решение получается и при ).

2 Применим ли принцип сжимающих отображений к заданному интегральному уравнению в пространстве Х при ? При с точностью до 0,01 найти приближенное решение и сравнить его с точным решением.

Пример 1 . (2)

Решение Определим отображение по формуле

.

Тогда исходное уравнение запишется в виде и искомое решение есть неподвижная точка отображения . Метрическое пространство является полным, поэтому если мы покажем, что – сжимающее отображение в себя, то можно будет применить принцип сжимающих отображений.

То, что отображение непрерывную на функцию переводит в непрерывную, в данном случае очевидно (а в общем следует из свойств интеграла, зависящего от параметра). Определим, при каких отображение является сжимающим.

Известно, что отображение

является сжимающим в , если , где . При этом константа Липшица . (Заметим, что это утверждение дает лишь достаточное условие сжимаемости). В данном случае , . Следовательно, является сжимающим при , то есть, в частности, при и .

Докажем, что не является сжимающим при . Если допустить, что – сжимающее, то для и некоторого должно выполняться неравенство

.

При , последнее неравенство примет вид:

.

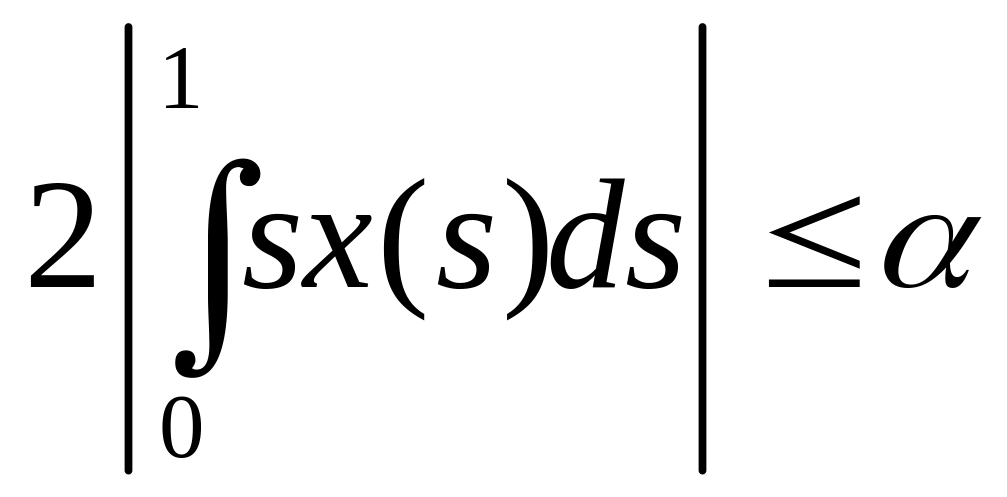Вычислив интеграл в левой части, получим . Это противоречие доказывает, что не является сжимающим при .

Решим уравнение (2) при . При этом отображение является сжимающим, а потому для нахождения приближенного решения можно воспользоваться методом итераций (последовательных приближений).

Поскольку выбирается произвольно, возьмём . Дальнейшие приближения находятся по формулам , .

Установим номер k, при котором элемент будет давать точность приближения 0,01. Используем оценку погрешности (х − точное решение)

.

В нашем случае . Кроме того, легко подсчитать, что . Следовательно, для нахождения нужного числа итераций имеем неравенство

,

Поскольку ему удовлетворяет, то будет приближенным решением исходного уравнения с точностью 0,01. Найдём :

,

.

Итак, приближённое решение с нужной точностью есть

Найдем точное решение данного уравнения. Из (2) следует, что его решение имеет вид

где , (3)

то есть вид . Подставив в (2), получим

.

Отсюда , . Следовательно, точное решение есть

Сравним его с приближённым:

.

Примечание Первую часть решения можно сократить, если воспользоваться тем фактом, что норма линейного оператора

в пространстве дается формулой:

.

Поскольку норма есть точная константа в неравенстве ограниченности, отображение является сжимающим тогда и только тогда, когда То же верно и для отображения (почему?).