МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Плоскость и прямая в пространстве
Учебно-методическое пособие для вузов.
Составители: Ф.В. Голованёва,
Е.В. Петрова
ВОРОНЕЖ
2011
Утверждено научно-методическим советом математического факультета
17 Февраля 2011 года
Протокол № 0500-02
Учебно-методическое пособие подготовлено на кафедре уравнений
в частных производных и теории вероятностей
математического факультета Воронежского госуниверситета
Рекомендуется для студентов 1-2 курсов очной формы обучения
химического факультета
Для специальности
«Химия, физика и механика материалов» 020900
1. Прямоугольные координаты в пространстве
Прямоугольная система координат
в пространстве определяется заданием
масштабной единицы измерения длин и
трех пересекающихся в одной точке
взаимно перпендикулярных осей:
,
и
.
Точка
- начало координат,
- ось абсцисс,
- ось ординат,
- ось аппликат.
Пусть
- произвольная точка пространства.
Проведем через точку
три плоскости, перпендикулярные
координатным осям
,
и
.
Точки пересечения плоскостей с осями
обозначим соответственно через
,
и
.
Прямоугольными координатами точки
называются числа
,
т.е. величины направленных отрезков
;
при этом
называется абсциссой,
- ординатой,
- аппликатой точки
.
Символ
обозначает, что точка
имеет координаты
.
Таким образом, при выбранной системе
координат каждой точке
пространства соответствует единственная
упорядоченная тройка чисел
- ее прямоугольные координаты и, обратно,
каждой упорядоченной тройке чисел
соответствует, и притом одна, точка
в пространстве.
Плоскости
,
,
называются координатными плоскостями.
Они делят все пространство на восемь
частей, называемых октантами.
Расстояние между двумя точками
и
определяется по формуле
.
В частности, расстояние точки от начала координат определяется по формуле
.
Если отрезок, концами которого служат
точки
и
,
разделен точкой
в отношении
,
то координаты точки
определяются по формулам
.
В частности, координаты середины отрезка определяются по формулам
.
Пример 1. Даны точки
и
.
На прямой
найти точку
,
делящую отрезок
в отношении
.
Решение.
Воспользуемся формулами деления отрезка в данном отношении:
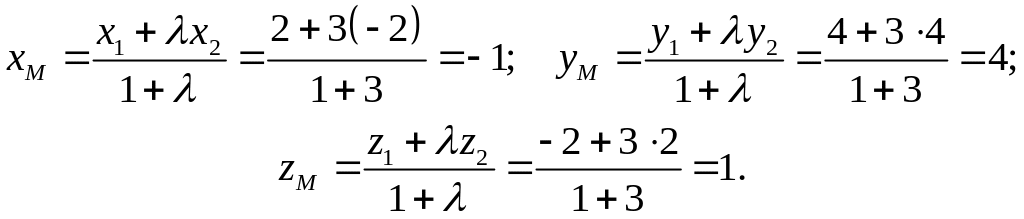
Следовательно, искомая точка
.
Пример 2. На оси
найти точку, равноудаленную от точек
и
.
Решение.
Пусть
- искомая точка. Для нее должно выполняться
равенство
.
Так как эта точка лежит на оси
,
то ее координаты
,
а потому имеем
.
Отсюда после возведения в квадрат получаем
,
или
,
т.е.
.
Таким образом, искомая точка
.
Задания для самостоятельного решения
1. Даны точки
и
.
Найти координаты точек
и
,
делящих отрезок
на три равные части.
2. Дан треугольник:
.
Показать, что угол
- тупой.
3. Найти координаты центра тяжести
треугольника с вершинами
.
4. В каком отношении точка
,
равноудаленная от точек
и
,
разделит отрезок оси
от начала координат до точки
?
5. На оси
найти точку, равноудаленную от точек
и
.
6. На плоскости
найти точку, равноудаленную от точек
,
и
.