4. Некоторые приложения скалярного произведения

Угол между векторами

Определение угла между ненулевыми векторами и :

, т.е. .

Отсюда следует условие перпендикулярности ненулевых векторов и :

.

Проекция вектора на заданное направление

Нахождение проекции вектора на направление, заданное вектором , может осуществляться по формуле

, т.е. .

Работа постоянной силы

Пусть материальная точка перемещается прямолинейно из положения в положение под действием постоянной силы , образующей угол с перемещением .

Из физики известно, что работа силы при перемещении равна

, т.е. .

Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора силы на вектор перемещения.

3. Векторное произведение векторов и его свойства

3.1. Определение векторного произведения

Три некомпланарных вектора , и , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора кратчайший поворот от первого вектора ко второму вектору виден совершающимся против часовой стрелки, и левую, если по часовой.

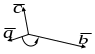правая тройка, левая тройка

Определение. Векторным произведением вектора на вектор называется вектор , который:

1) перпендикулярен векторам и , т.е. и ;

2) имеет длину, численно равную площади параллелограмма, построенного на векторах и как на сторонах, т.е.

, где ;

3) векторы , и образуют правую тройку.

Векторное произведение обозначается или .

Из определения векторного произведения непосредственно вытекают следующие соотношения между ортами , и :

, , .

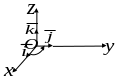
3.2. Свойства векторного произведения

1. При перестановке сомножителей векторное произведение меняет знак, т.е. .

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т.е. .

3. Два ненулевых вектора и коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т.е. .

В частности, .

4. Векторное произведение обладает распределительным свойством:

.

3.3. Выражение векторного произведения через координаты

Мы будем использовать таблицу векторного произведения векторов , и :

Пусть заданы два вектора и . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойствам векторного произведения):

,

т.е.

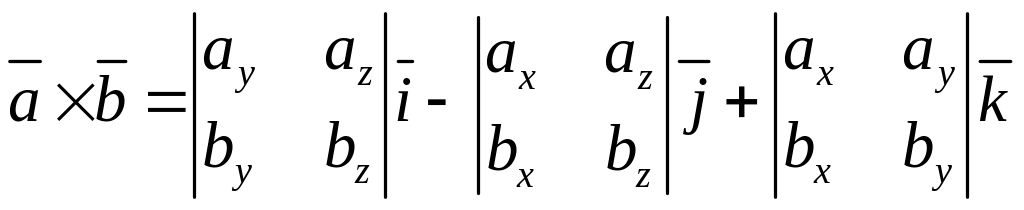. (8)

Полученную формулу можно записать еще короче:

, (9)

так как правая часть равенства (8) соответствует разложению определителя третьего порядка по элементам первой строки. Равенство (9) легко запоминается.

3.4. Некоторые приложения векторного произведения

Установление коллинеарности векторов

Если , то (и наоборот), т.е.

.

Нахождение площади параллелограмма и треугольника

Согласно определению векторного произведения векторов и , т.е. . И, значит, .

Определение момента силы относительно точки

Пусть в точке приложена сила и пусть - некоторая точка пространства.

Из физики известно, что моментом силы относительно точки называется вектор , который проходит через точку и:

1) перпендикулярен плоскости, проходящей через точки , , ;

2) численно равен произведению силы на плечо

;

3) образует правую тройку с векторами и .

Стало быть, .

Нахождение линейной скорости вращения

Скорость точки твердого тела, вращающегося с угловой скоростью вокруг неподвижной оси, определяется формулой Эйлера , где , где - некоторая неподвижная точка оси.