2.2. Таблица неопределенных интегралов
Так как интегрирование есть операция обратная дифференцированию, то всякую формулу для производной конкретных функций можно обратить:
.
Поэтому таблицу основных интегралов получаем из таблицы производных, записав, её справа налево:
1.
.
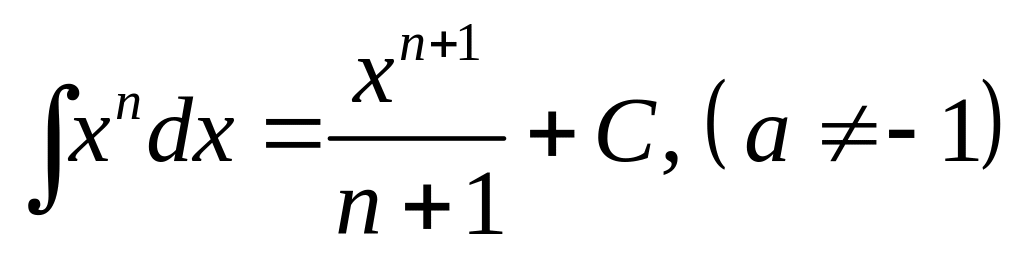2.
.
3.
.
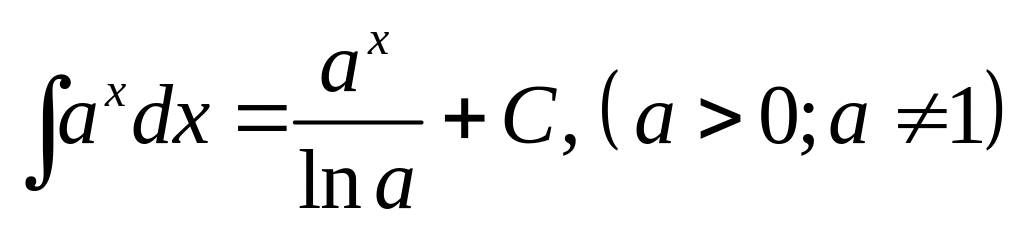4.
.
5.
.
6.
.
7.
.
8.
.
9.
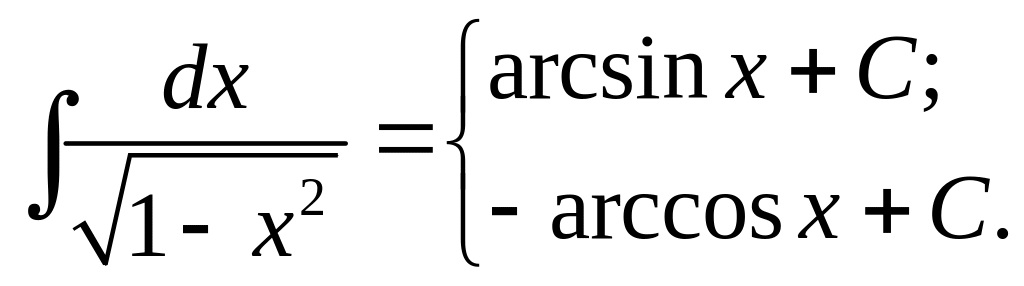
10.
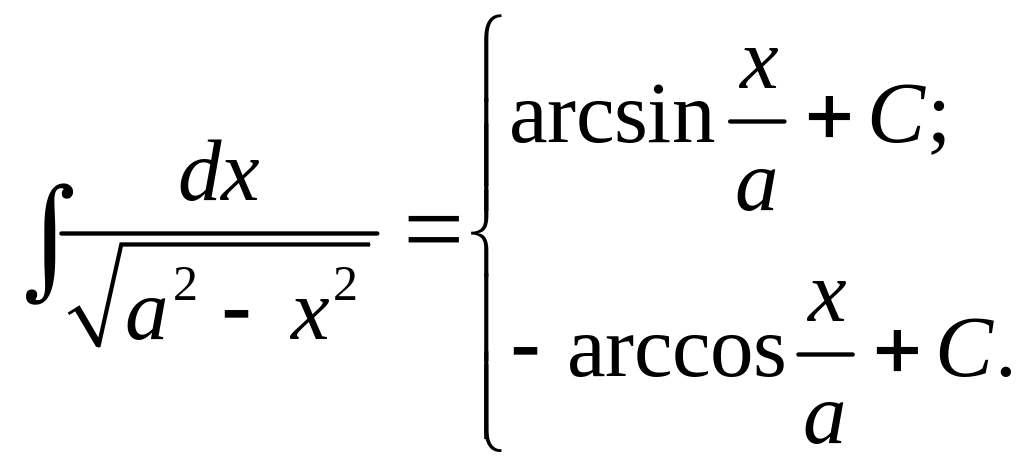
11.
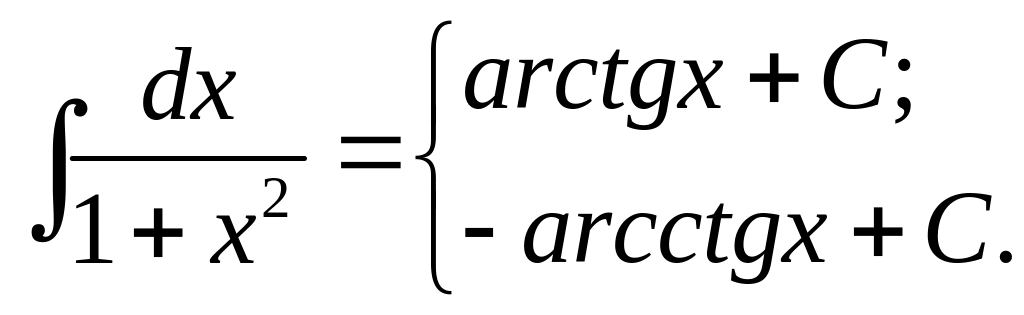
12.
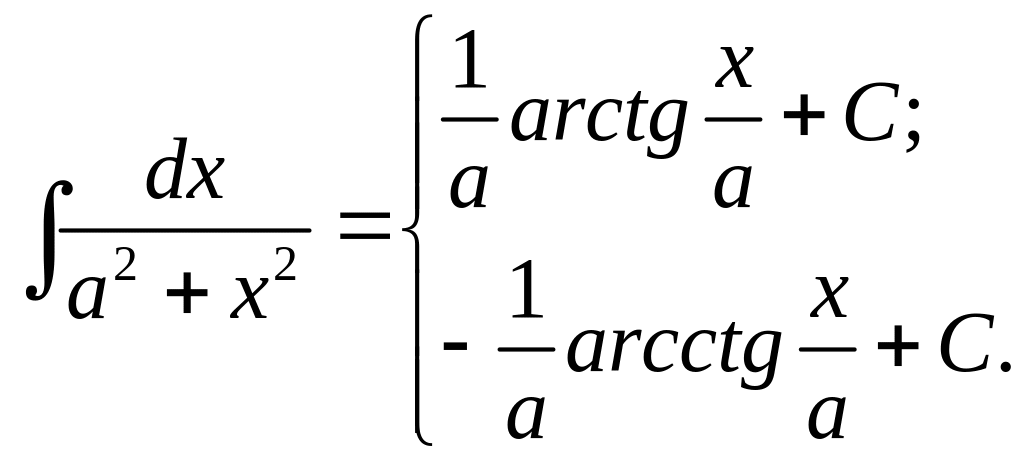
13.
.
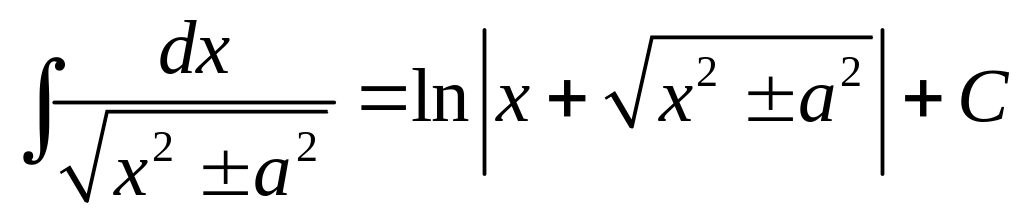14.
.
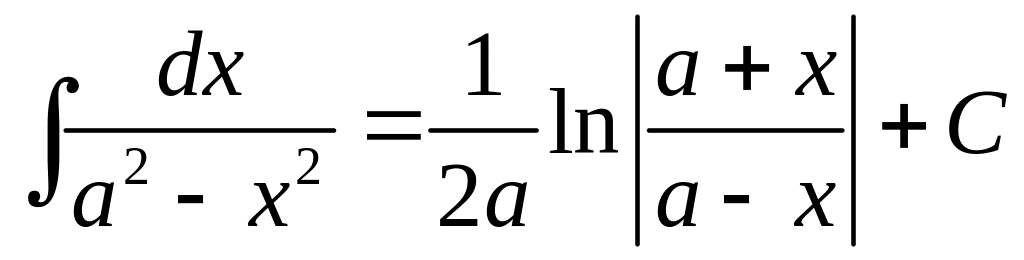Все эти формулы проверяются дифференцированием правой части.
Примеры. Вычислить неопределенные интегралы.
1.
.
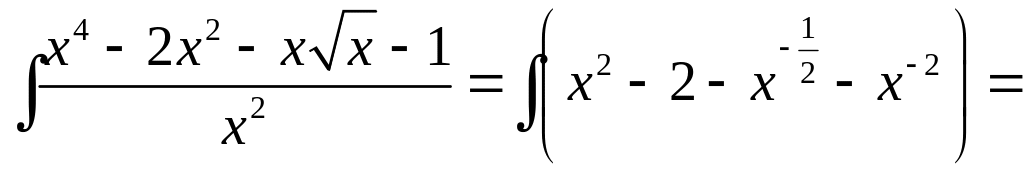
2.
.
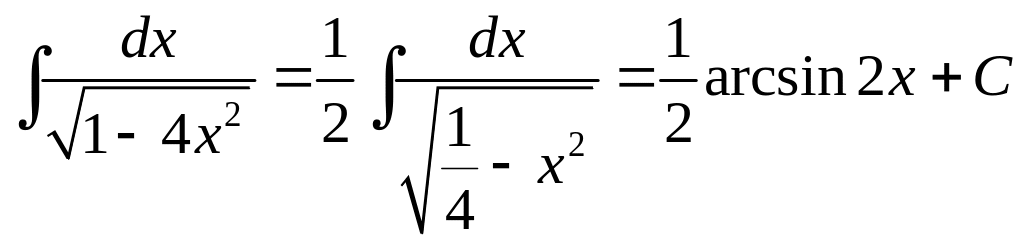Интегралы, содержащиеся в таблице, называются табличными и их надо твёрдо запомнить, т.к. вычисление интеграла сводится к последовательным операциям, результатом которых являются приведения заданного интеграла к табличному (если это возможно).
2.3. Непосредственное интегрирование
.
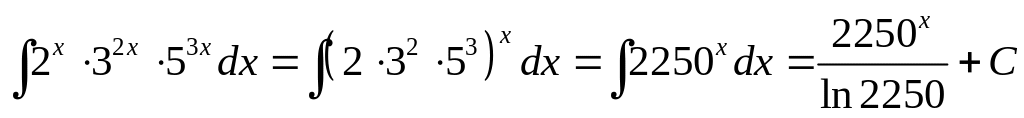2.4. Интегрирование с помощью замены переменной
Одним из самых сильных методов интегрирования является метод замены переменной.
Пусть надо вычислить интеграл
. (8)
Часто
его можно упростить, введя вместо
новую переменную
,
положив
и
. (9)
Для преобразования неопределённого интеграла (8) к новой переменной по формуле (9) достаточно преобразовать к новой переменной его подынтегральное выражение:
(10)
В
формуле (10) предполагается, что
непрерывна на некотором промежутке оси
Ох, а функции
и
непрерывны на соответствующем промежутке
изменения
.
Это равенство надо понимать так: после
интегрирования левой части по
и подстановки
мы должны получить тождество.
Замечание 1. Часто вместо подстановки (4) употребляют обратную:
;
. (11)
Замечание
2. Так как
,
то если
,
из (10) следует:
.
Таким образом, вид неопределённого интеграла не зависит от выбора аргумента интегрирования. Этот факт используется при интегрировании способом подведения под знак дифференциала.
Примеры.
1.
.
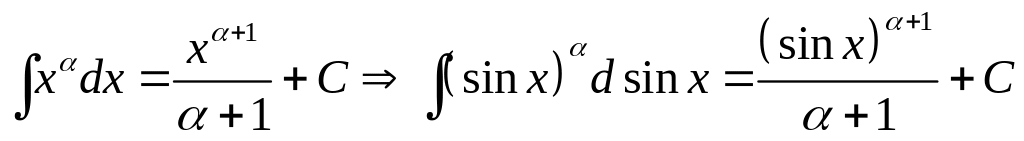2.
.
3.
.
4.
.
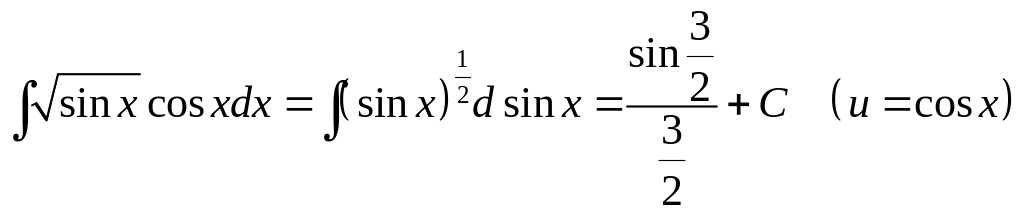5.
.
Вообще:
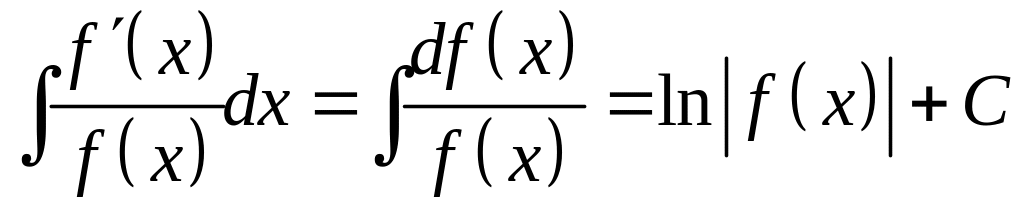. (12)
Если в числе стоит производная знаменателя, то интеграл от дроби равен логарифму от модуля знаменателя.
6.
.
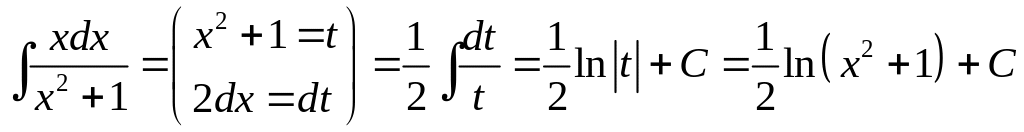2.5. Правило интегрирования по частям
Пусть
функции
и
имеют непрерывные производные. Тогда
по правилу дифференцирования произведения
имеем:
.
Интегрируем обе части равенства по :
. (13)
Эта
формула называется формулой интегрирования
по частям. Формула сводит вычисление
интеграла
к вычислению интеграла
,
который может оказаться проще исходного.
При этом за
обычно выбирают множитель подынтегрального
выражения, который при дифференцировании
упрощается, а за
– множитель, который нетрудно
проинтегрировать.
Примеры. Вычислить неопределенные интегралы, используя метод интегрирования по частям.
1.
.
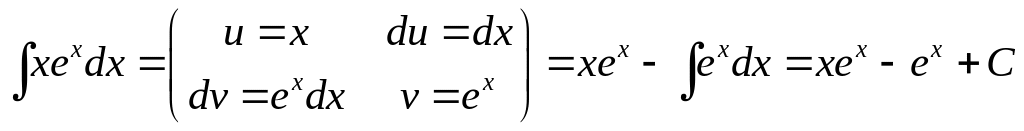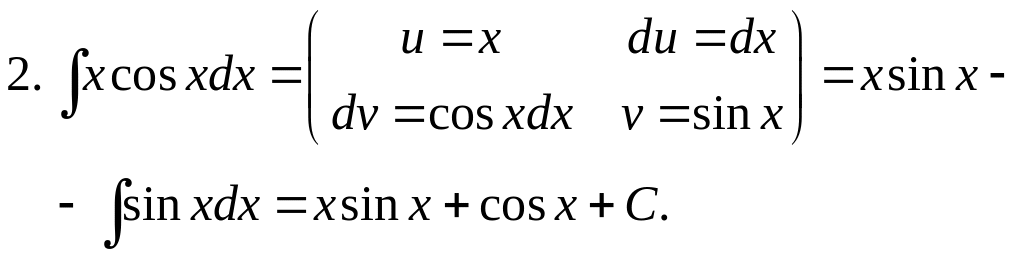
3.
.
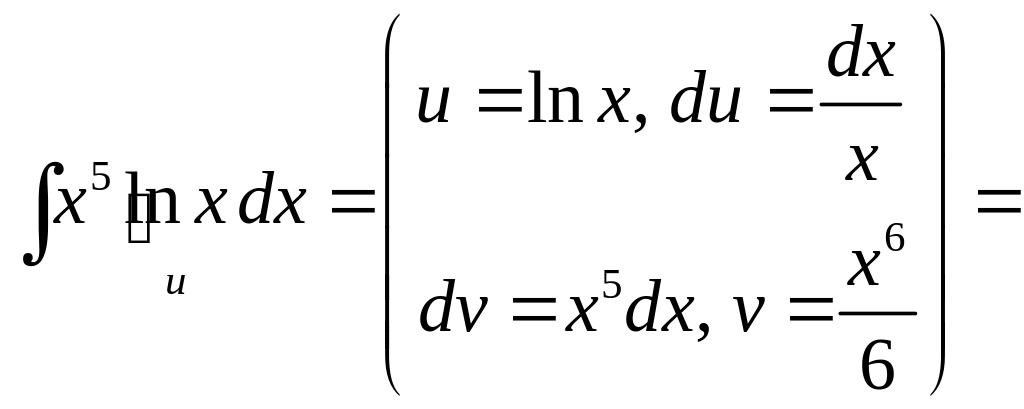
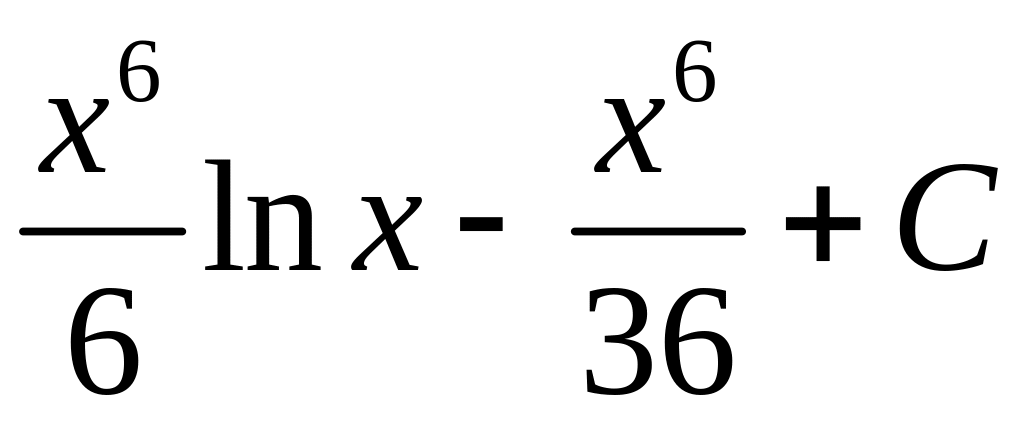Интегрирование по частям приводит к успеху при интегрировании выражений вида:
,
,
,
.
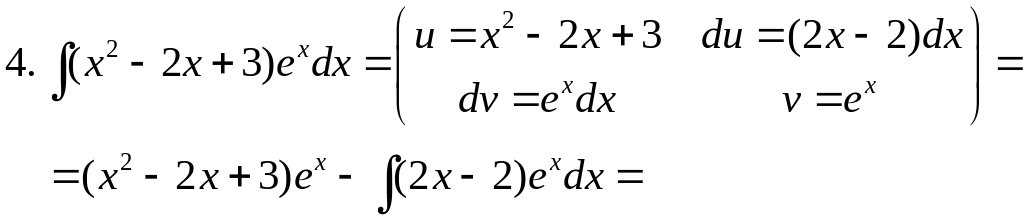
Применим ко второму интегралу еще раз формулу интегрирования по частям
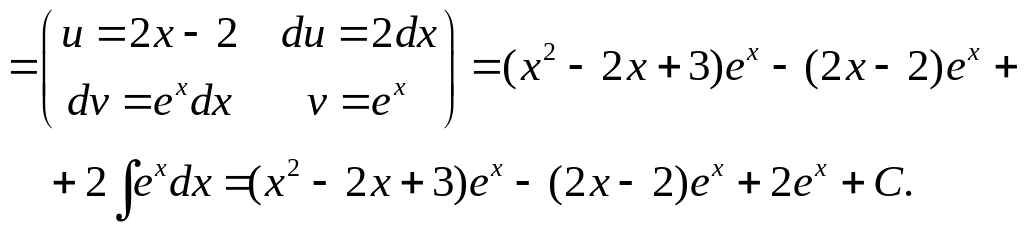
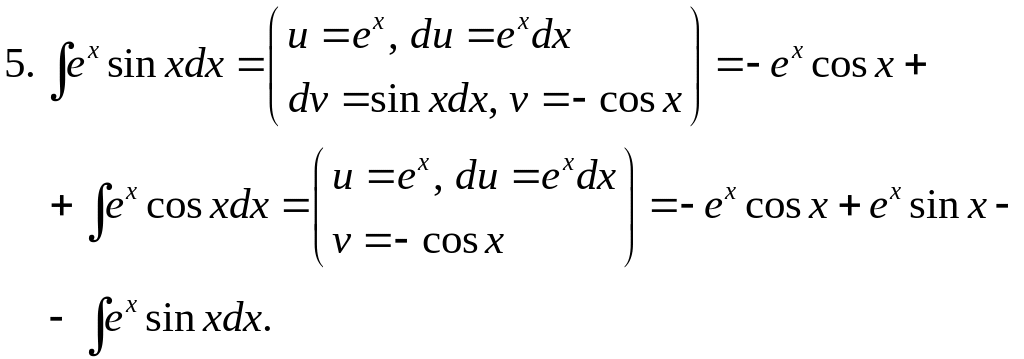
Получили
интеграл, равный данному. Обозначив его
за
,
получим равенство
.
Перенося в левую часть равенства, имеем
.
Окончательно:
.
2.6. Об интегрировании в элементарных функциях
Операция дифференцирования элементарной функции снова приводит к элементарным функциям. Интегрирование элементарной функции часто приводит к неэлементарным функциям, т.е. функциям задаваемых одной формулой, содержащей конечное число операций. Например, доказано, что такими являются интегралы:
- интеграл Пуассона,
- интегральный логарифм,
- интегралы Френеля,
- интегральный синус и т.д.
Первообразные для этих функций существуют, но не выражаются через элементарные функции. Наиболее важные из этих первообразных протабулированы.
В связи со сказанным полезно рассмотреть классы функций, первообразные которых являются элементарными функциями.