
- •1. Дифференциальные уравнения первого порядка
- •1.1 Задачи, приводящие к дифференциальным уравнениям.
- •1.2.Основные понятия теории дифференциальных уравнений.
- •1.3. Метод изоклин
- •1.4. Уравнения с разделяющимися переменными и однородные дифференциальные уравнения
- •Пример1. Найти общий интеграл уравнения
- •Реш ение.
- •Р е ш е н и е. Запишем уравнение в виде
- •Отсюда интегрированием находим
- •1.6 Уравнения в полных дифференциалах
- •1.7 Уравнения, неразрешенные относительно производной
- •2.Дифференциальные уравнения высших порядков
- •2.2. Уравнения, допускающие понижение порядка.
- •Пример 4. Решить уравнение
- •2.3. Линейные однородные уравнения высших порядков
- •2.4. Интегрирование лоду с постоянными коэффициентами
- •2 .5.Линейные неоднородные дифференциальные уравнения со специальной правой частью.
- •2.6.Уравнения Эйлера
- •3.Системы дифференциальных уравнений.
- •4.Элементы теории устойчивости
- •4.1. Предварительные замечания
- •4.2. Устойчивость по Ляпунову. Основные понятия, определения
- •5.Задачи для самостоятельного решения
- •4.Краснов м.Л. Обыкновенные дифференциальные
- •Дифференциальные уравнения первого порядка.
- •5.Задачи для самостоятельного решения
4.2. Устойчивость по Ляпунову. Основные понятия, определения
Р
dx/dt=f(t,x); (2.1)
где
функция f(t,х)
определена и непрерывна для
![]() и х из некоторой области D
и имеет ограниченную частную производную
f/х.
Пусть функция
и х из некоторой области D
и имеет ограниченную частную производную
f/х.
Пусть функция
![]() есть решение уравнения, удовлетворяющее
начальному условию
есть решение уравнения, удовлетворяющее
начальному условию
![]() Пусть, далее, функция x=x(t)
есть решение того же уравнения,
удовлетворяющее другому начальному
условию
Пусть, далее, функция x=x(t)
есть решение того же уравнения,
удовлетворяющее другому начальному
условию
![]() Предполагается, что решения (t)
и x(t)
определены для всех tto,
т. е. неограниченно продолжаемы вправо.
Предполагается, что решения (t)
и x(t)
определены для всех tto,
т. е. неограниченно продолжаемы вправо.
Определение. Решение x=(t)
уравнения (5.5) называется
устойчивым по Ляпунову при
![]() ,если
для любого >0
существует =()>0
такое, что для всякого решения x=x(t)
этого уравнения из неравенства
,если
для любого >0
существует =()>0
такое, что для всякого решения x=x(t)
этого уравнения из неравенства
![]() (5.6)
(5.6)
следует неравенство
5.7![]()
для всех tto (всегда можно считать, что ).
Это значит, что решения, близкие по начальным значениям к решению х=(t), остаются близкими и при всех tto.
Г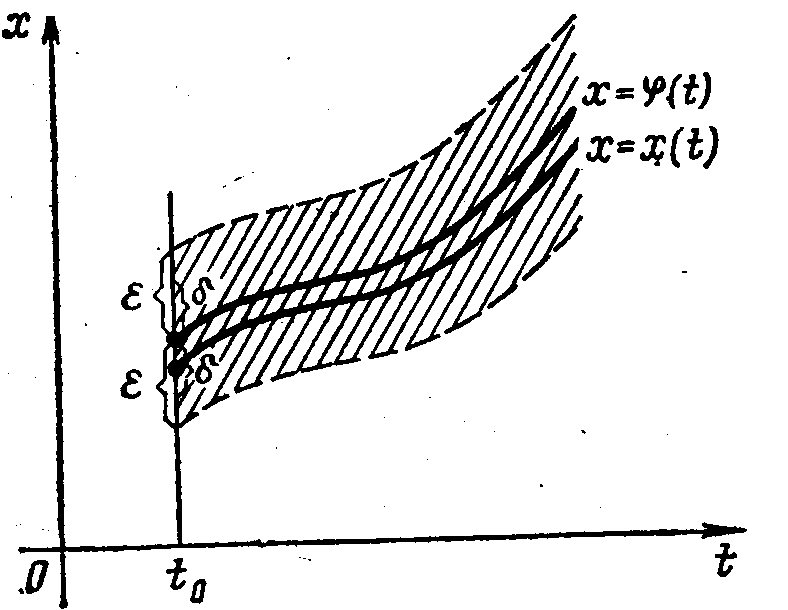 еометрически
это означает следующее. Решение
x=(t)
уравнения (5.5) устойчиво,
если, какой бы узкой ни была -полоска,
содержащая кривую х=(t),
достаточно близкие к ней в начальный
еометрически
это означает следующее. Решение
x=(t)
уравнения (5.5) устойчиво,
если, какой бы узкой ни была -полоска,
содержащая кривую х=(t),
достаточно близкие к ней в начальный
момент t=to интегральные кривые x=x(t) уравнения целиком содержатся в указанной -полоске при всех tto (рис.2).
Е
Рис. 4
Неустойчивым следует считать и решение, не продолжаемое вправо при .
Определение 5.2. Решение x=(t) уравнения (5.5) называется асимптотически устойчивым, если
1) решение х = (t) устойчиво,
2) существует 61>0
такое, что для любого решения x=x(t)
уравнения (5.5), удовлетворяющего
условию
![]() ,
имеем
,
имеем
![]()
Это означает, что все решения x=x(t), близкие по начальным условиям к асимптотически устойчивому решению x=(t), не только остаются близкими к нему при t to, но и неограниченно сближаются с ним при . Вот простая физическая модель. Пусть шарик лежит на дне полусферической лунки (находится в положении равновесия). Если малым возмущением вывести шарик из этого положения, то он будет колебаться около него. При отсутствии трения, положение равновесия будет устойчивым, при наличии трения колебания шарика будут уменьшаться с возрастанием времени, т. е. положение равновесия будет асимптотически устойчивым.
Пример.1. Исследовать на устойчивость тривиальное решение х0 уравнения.
dx/df=0. (*)
Решение х0, очевидно,
удовлетворяет начальному условию
![]() .
Решение уравнения (*),
удовлетворяющее начальному условию
.
Решение уравнения (*),
удовлетворяющее начальному условию
![]() ,
имеет вид хх0.
Легко видеть (рис. 5),
,
имеет вид хх0.
Легко видеть (рис. 5),
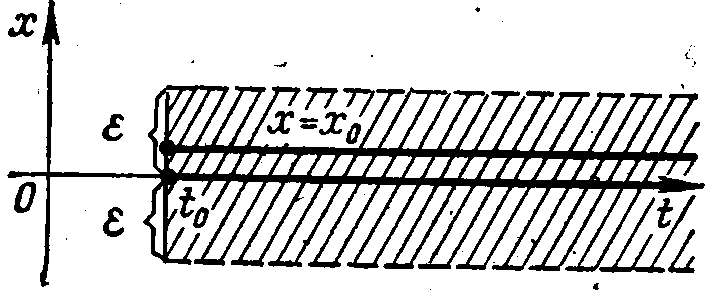
Рис. 5
что, какова бы ни была -полоска вокруг интегральной кривой х=0, существует >0, например =, такое, что любая интегральная кривая х=х0, для которой | х0-0 | <, целиком содержится в указанной -полоске для всех tto. Следовательно, решение х0 устойчиво. Асимптотической устойчивости нет, поскольку прямая х=х0 при не стремится к прямой х=0.
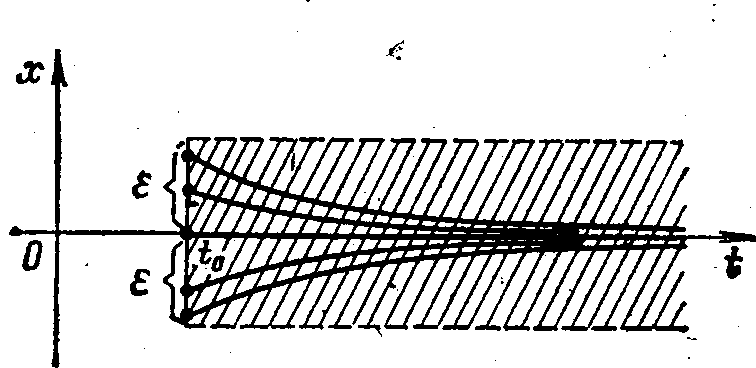
Рис. 6
Пример 1. Исследовать на устойчивость тривиальное решение х0 уравнения
dx/dt=-a2x (a==const), (1)
решение уравнения (1), удовлетворяющее начальному условию , имеет вид
![]()
Возьмем любое >0 и рассмотрим разность решений х(t) и (t)0:
![]() (***)
(***)
Поскольку
![]() для всех tto,
из выражения (***) следует,
что существует >0,
например =,
такое, что при |x0-0|<=.
имеем
для всех tto,
из выражения (***) следует,
что существует >0,
например =,
такое, что при |x0-0|<=.
имеем
![]()
С![]() огласно
определению (5.1) это
означает, что решение (t)0
уравнения (**) устойчиво.
огласно
определению (5.1) это
означает, что решение (t)0
уравнения (**) устойчиво.
Кроме того, имеем
![]()
Рис. 7.
поэтому решение (t)0 асимптотически устойчиво (рис. 6).
Пример 5.3. Показать, что решение (t)0 уравнения
dx/dt=a2x
неустойчиво.
В самом деле, при сколь угодно малом
![]() решение
решение
![]() этого уравнения не удовлетворяет условию
этого уравнения не удовлетворяет условию
![]() при достаточно больших t>to.
Более того, при любых x00
имеем
при достаточно больших t>to.
Более того, при любых x00
имеем
![]() (рис. 7)
(рис. 7)
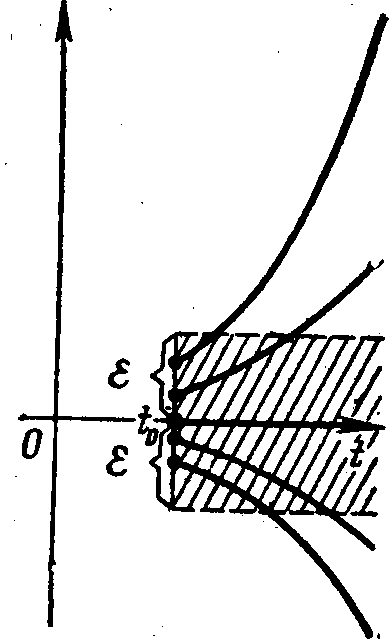
. .
Р
5.8
![]()
где функции
h определены для
![]() из некоторой области D
изменения
из некоторой области D
изменения
![]() и удовлетворяют условиям
теоремы существования и единственности
решения задачи Коши. Предположим,
что все решения системы (5.8)
неограниченно продолжаемы вправо при
и удовлетворяют условиям
теоремы существования и единственности
решения задачи Коши. Предположим,
что все решения системы (5.8)
неограниченно продолжаемы вправо при
![]() .
.
Определение. Решение
![]() системы (5.8) называется
устойчивым по Ляпунову при
для любого >0
существует =()>0
такое, что для всякого решения хi(t)
(i=l,
2,..., n) той же системы, начальные
значения которого удовлетворяют
неравенствам:
системы (5.8) называется
устойчивым по Ляпунову при
для любого >0
существует =()>0
такое, что для всякого решения хi(t)
(i=l,
2,..., n) той же системы, начальные
значения которого удовлетворяют
неравенствам:
![]()
выполняются неравенства
5.9![]()
для всех tt0 близкие по начальным значениям решения остаются близкими для всех tt0.
Если при сколь угодно малом >0, хотя бы для одного решения xi(t), i==l, 2, ..., n, неравенства (5.9) не выполняются, то решение i(t) называется неустойчивым.
Определение. Решение i(t), I = 1, 2, ..., n, системы (5.8) называется асимптотически устойчивым, если:
1) решение это устойчиво,
2) существует i> 0 такое, что всякое решение xi(t), i =1, 2,..., n, системы, для которого
![]()
удовлетворяет условию
![]()
Из устойчивости нетривиального решения дифференциального уравнения не следует ограниченности этого решения. Рассмотрим например, уравнение dx/dt=1. Решением этого уравнения, удовлетворяющим условию x(o)=o, является функция (t)=t. Решение, удовлетворяющее начальному условию х(0)=x0, имеет вид x(t)=t+x0. Геометрически очевидно (рис. 8), что для всякого >0 существует >0, например =, такое, что любое решение х(t) уравнения, для которого верно неравенство |x0-0|< удовлетворяет условию | х(t) - t|< t0.
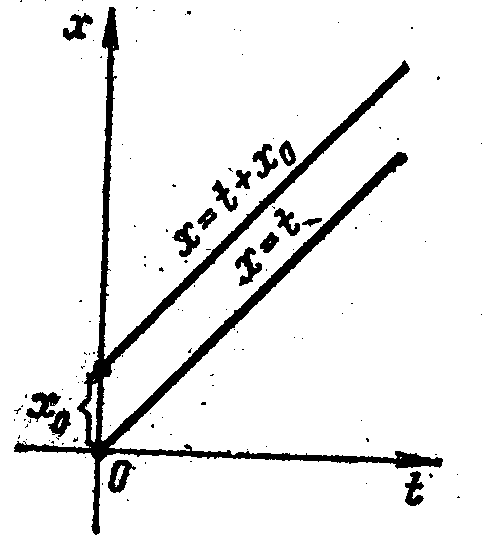
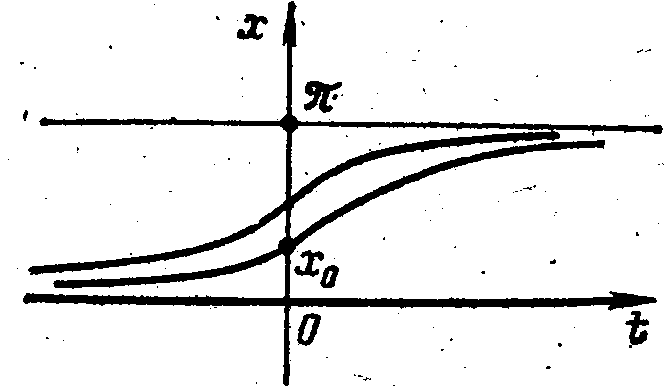
Рис.8 Рис. 9
Последнее означает, что решение (t)=t устойчиво по Ляпунову, однако это решение является неограниченным при .
И
5.10
dx/dt= sin2 x.
О
5.11
x= , =± 1, ± 2. ....
и
5.12
х= arcctg (ctg x0 – t), x.
Все решения (5.11) и
(5.12) ограничены на (![]() .)
Однако решение (t)0
неустойчиво при
.
так как при любом
.)
Однако решение (t)0
неустойчиво при
.
так как при любом
![]() имеем
имеем
![]() (рис. 9).
(рис. 9).
Таким образом, ограниченность и устойчивость решений являются понятиями, независимыми друг от друга.
