11

КОНТРОЛЬНАЯ РАбОТА №1

Цель работы – закрепить материал по разделам классической теории линейных систем автоматического управления, основанной на структурном представлении и преобразовании математического описания САУ, на базе понятия передаточной функции и частотных методов анализа и синтеза.

Исходные данные

Вариант 13

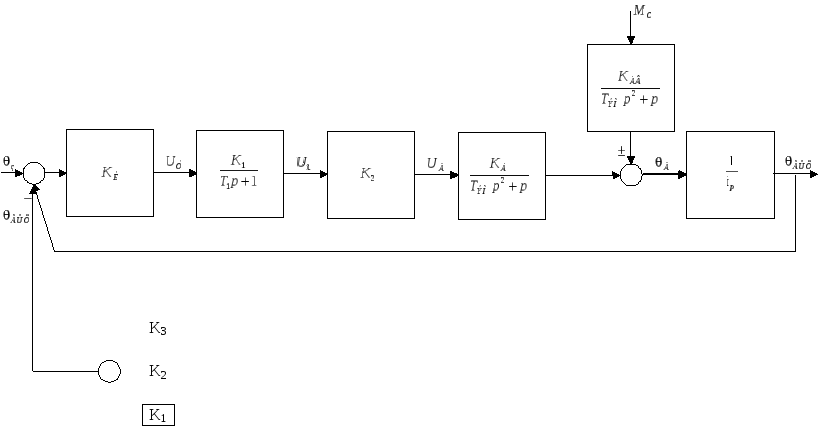
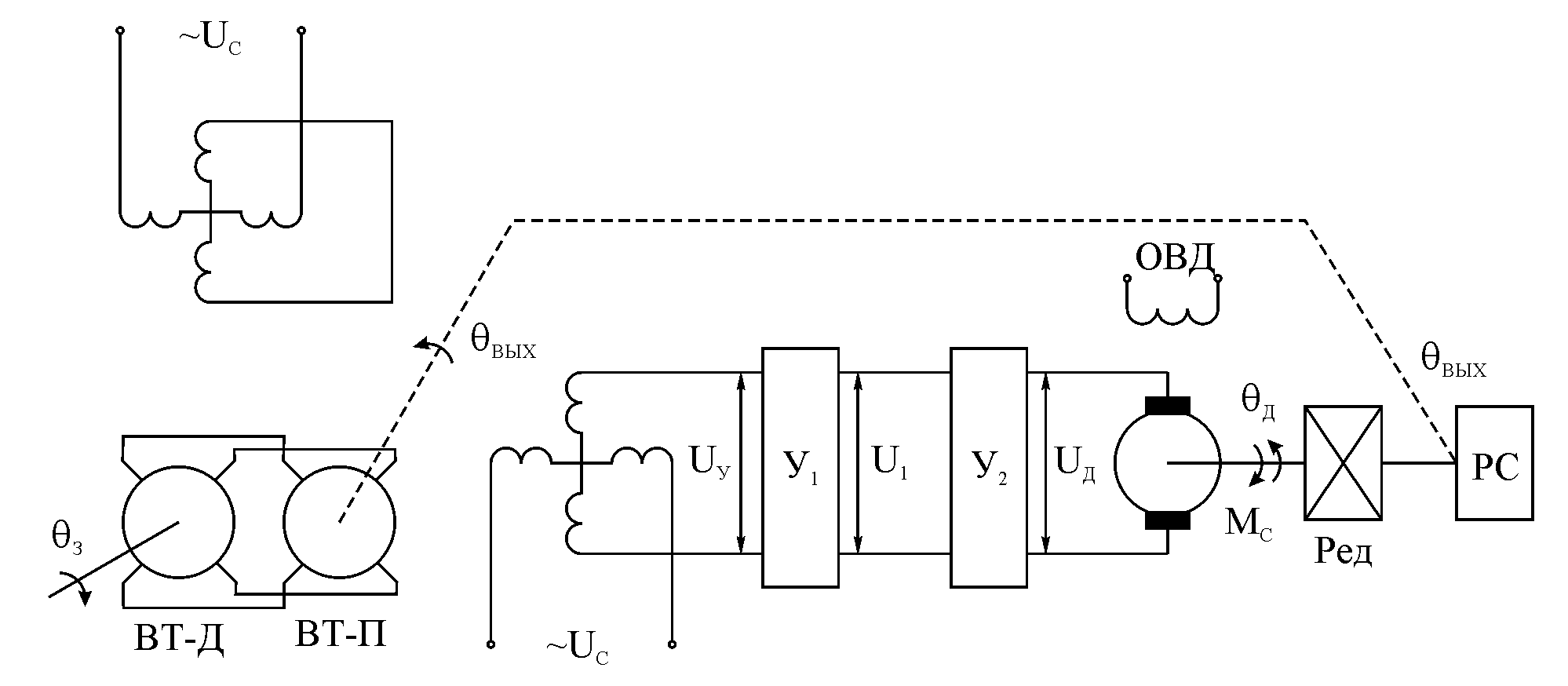Функциональная схема следящего электропривода

Параметры: K_и =20 в/рад; K₁ = 50; K₂ = 1; i_P = 50;

K_Д = 0,2 (Вс)^–1; K_ДВ = 0,3 (Нмс)^–1; T₁ = 3,5 с10^–2; Т_ЭМ = 0,35 с.

Связь между входными и выходными переменными:

1: измеритель рассогласования: ,

2: усилитель У₁ совместно с демодулятором:

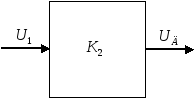
3: усилитель мощности У₂:

4: исполнительный двигатель:

5: редуктор:

Решение

1. По дифференциальным уравнения, соответствующим заданной функциональной схеме, записать передаточные функции и составить структурные схемы для каждого элемента системы.

Запишем уравнения элементов САУ в операторном виде:

1: ,

2:

3:

4:

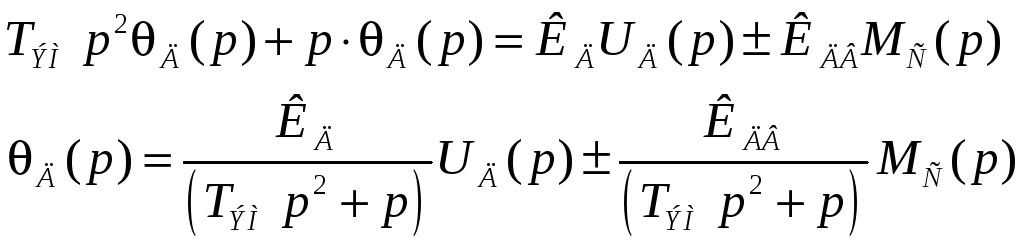
5:

структурные схемы:

1:	2:
3:	4:
5:

2. Составить структурную схему системы автоматического управления в целом.

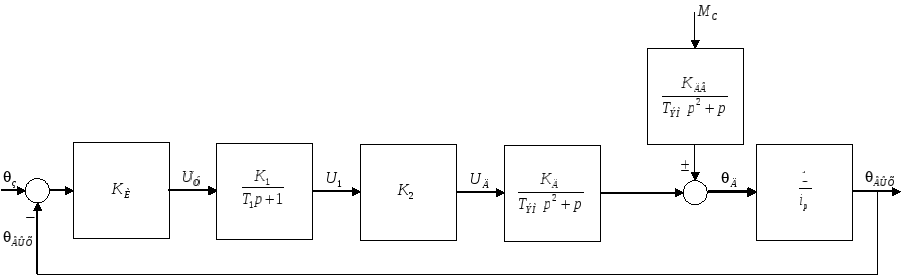
3. Определить передаточные функции разомкнутой и замкнутой системы по управляющему и возмущающему воздействиям, а также передаточные функции по ошибке от этих воздействий.

Преобразуем структурную схему к стандартному виду:

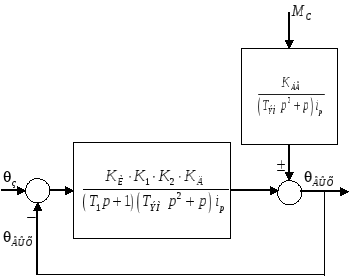
Передаточная функция разомкнутой системы:

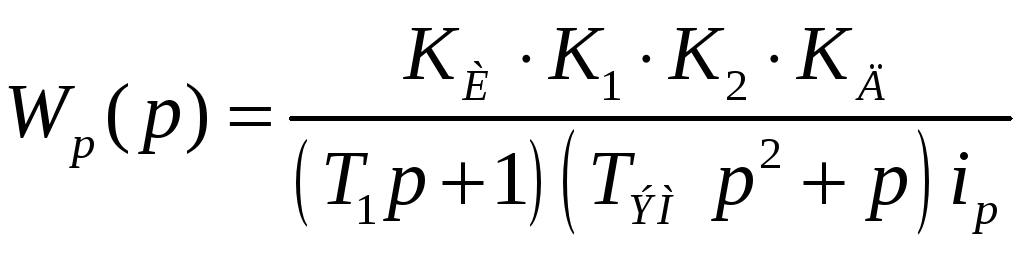
Передаточная функция замкнутой системы по управлению:

Передаточная функция замкнутой системы по возмущению:

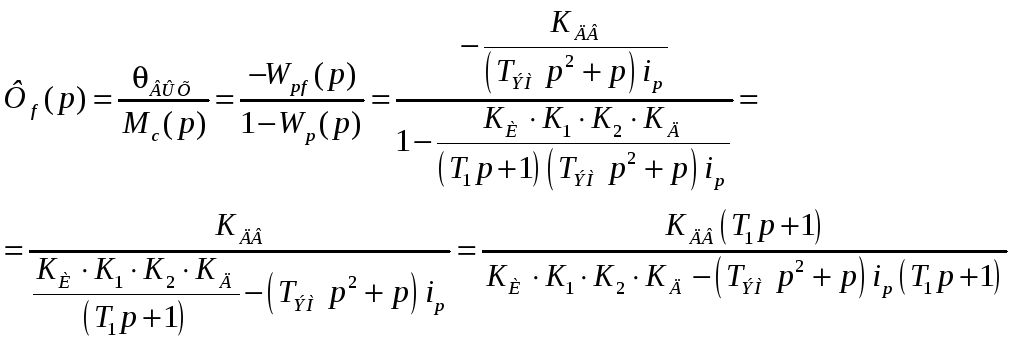
Передаточная функция замкнутой системы по ошибке от управления

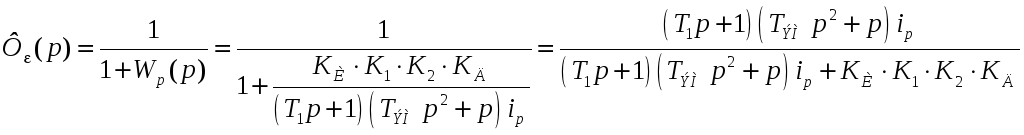
Передаточная функция замкнутой системы по ошибке от возмущения:

4. Исследовать систему на устойчивость методом Гурвинца.

Запишем характеристический полином замкнутой системы:

Подставим значения параметров:

Матрица главного определителя:

Проверим положительны ли все диагональные определители:

Следовательно система является устойчивой.

5. Определить установившиеся ошибки в системе от постоянных (единичных) управляющего и возмущающего воздействий.

Установившиеся ошибки в системе от единичных воздействий определяться коэффициентом С₀=Ф(0).

Установившаяся ошибка от управляющего воздействия

Установившаяся ошибка от возмущающего воздействия

КОНТРОЛЬНАЯ РАбОТА №2

Цель работы – исследование системы автоматического управления методом, основанным на понятии пространства состояний.

Решение

1. Составить уравнения состояния по структурной схеме системы автоматического управления.

Порядок характеристического полинома системы n=3. Соответственно число переменных состояния должно быть 3.

Для каждого интегратора запишем дифференциальное уравнение первого порядка:

В векторно-матричной форме система имеет вид:

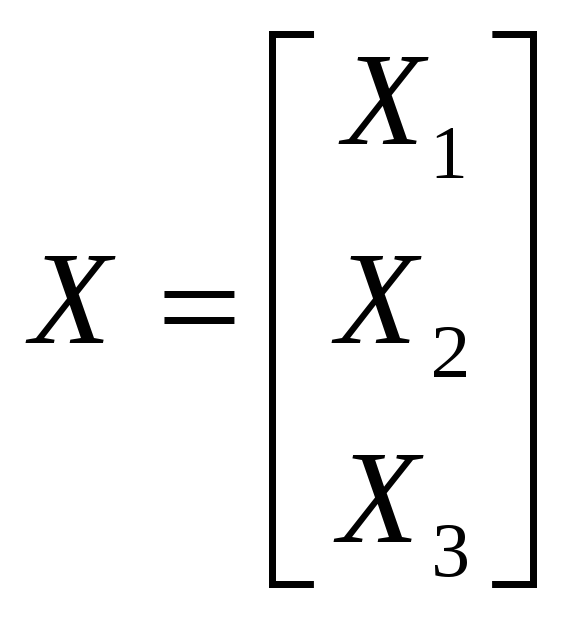
Уравнение наблюдения будет иметь вид:

2. Составить уравнение состояния по передаточной функции замкнутой системы автоматического управления по управляющему воздействию.

Передаточная функция замкнутой системы по управлению

Этой передаточной функции соответствует дифференциальное уравнение в операторной форме

Сделаем замену:

Уравнение примет вид:

Пусть , уравнение наблюдения будет иметь вид:

В векторно-матричной форме уравнения запишутся в виде:

3. Определить устойчивость системы, используя уравнения состояния, полученные в пункте 2.

Вычислим по матрице A характеристический полином системы D=det(pE – A).

Анализ устойчивости выполним по критерию Гурвинца.

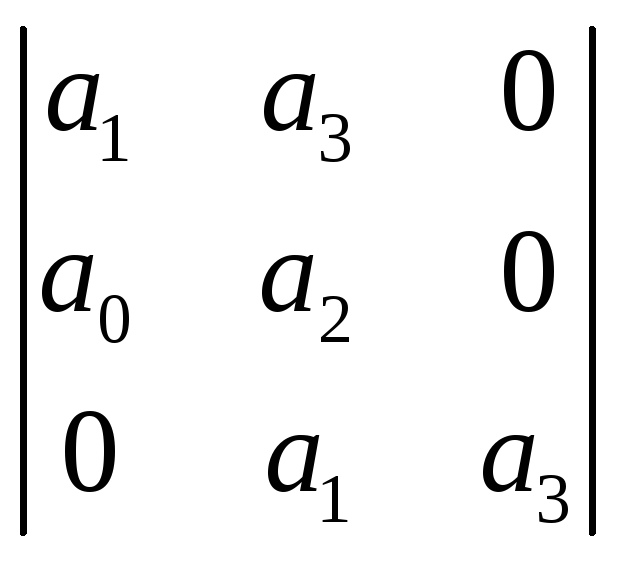
a₀>0; (a₁a₂ – a₀a₃)>0

Условие выполняется, значит система устойчива.

4. Произвести синтез модального регулятора при следующих условиях:

- все переменные состояния доступны изменению;

- синтез регулятора производится только для управляющего воздействия, возмущающее воздействие равно нулю;

желаемый характеристический полином замкнутой системы принимаем в виде полинома соответствующего фильтру Баттерворта 3-го порядка

,

Входная матрица системы:

Собственная матрица параметров системы:

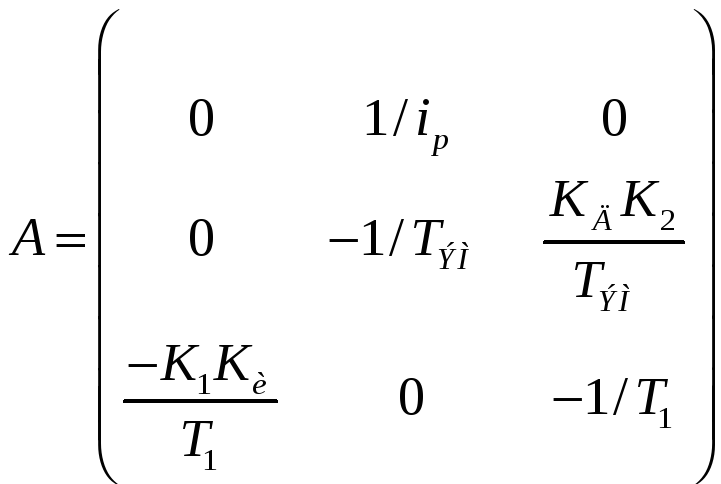
Матрица искомых коэффициентов обратных связей по переменным состояния имеет вид

K=[K₁ K₂ K₃]

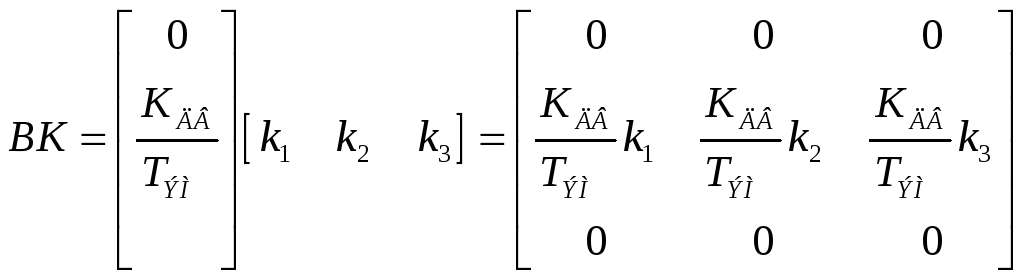
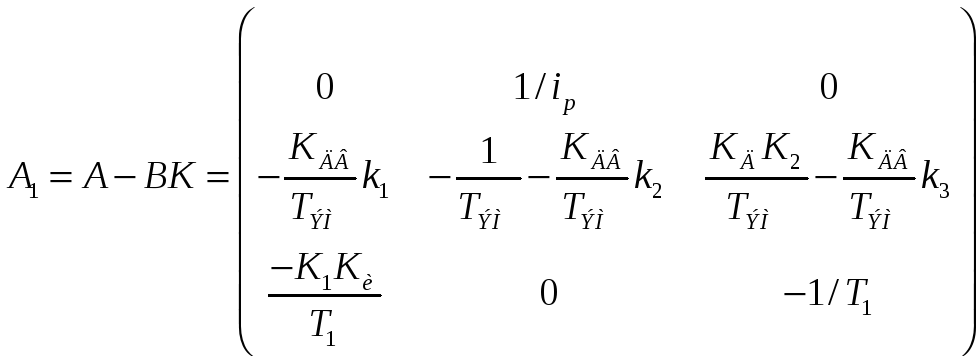
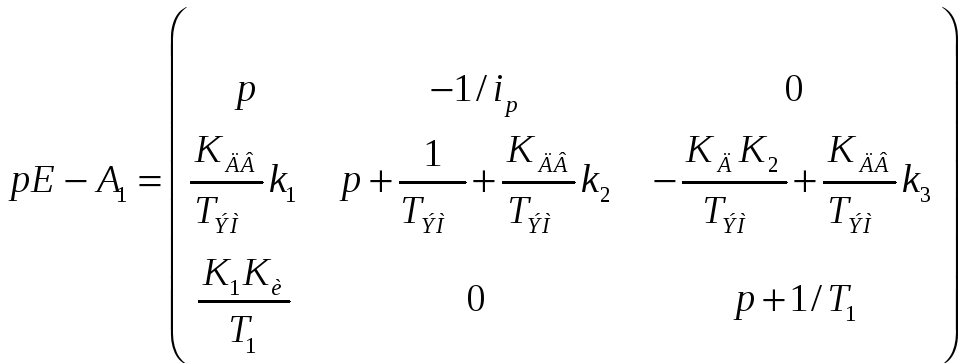
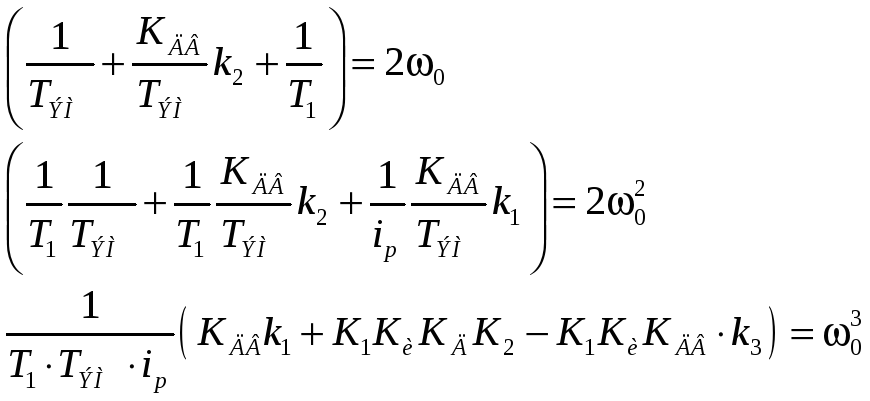
подставим числа:

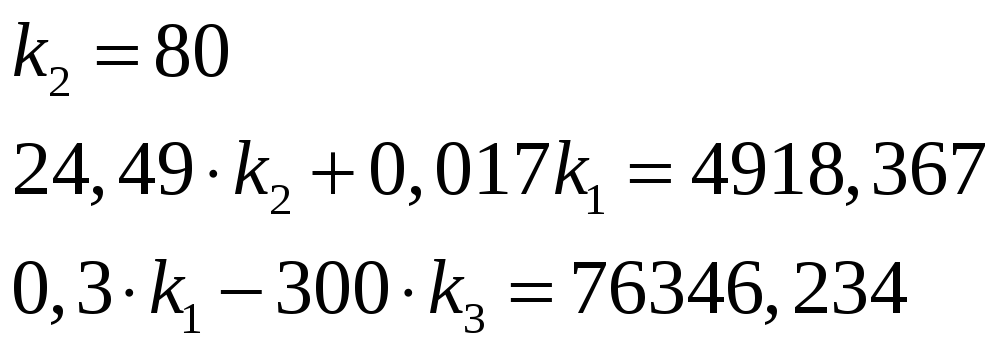
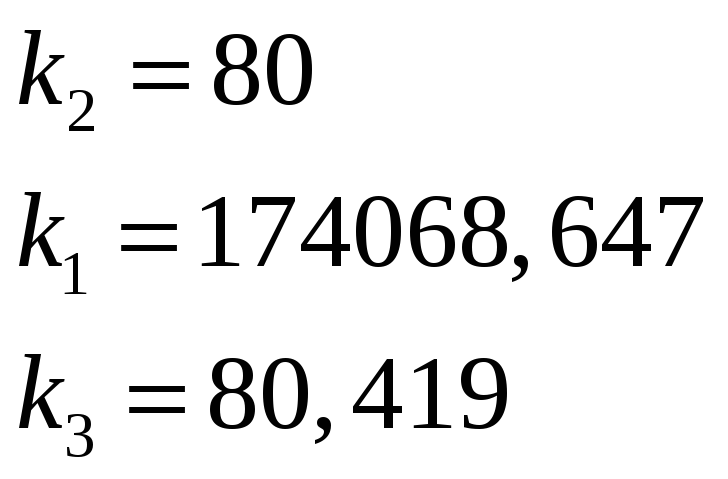
Структурная схема имеет вид: