
4.Исследование устойчивости объекта
Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо воздействия.
Если система неустойчива, то достаточно любого толчка, чтобы в ней начался расходящийся процесс ухода из исходного установившегося состояния.
Исследуем заданный объект на устойчивость. Собираем структурную схему на ЭВМ в пакете Siam. Подставляя формулы в передаточные функций получаем следующий график (рис.4).
ЭВМ выдает ЛАХ и ЛФХ неустойчивой системы, из графика видно, что система при исходных данных абсолютно не устойчива, т.к. ωср>ωкр
Для
того, чтобы добиться заданных показателей
качества (tp
= 2,с; коэффициент перерегулирования
![]() =25%
=25%![]() 30%)
вводим корректирующее устройство.
30%)
вводим корректирующее устройство.
Для ввода корректирующего устройства необходимо найти общую передаточную функцию всей системы.
Для удобства выполнения расчетов обозначим каждый блок отдельной буквой.
Д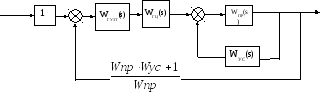 ля
составления общей передаточной функции
необходимо преобразовать структурную
схему:
ля
составления общей передаточной функции
необходимо преобразовать структурную
схему:
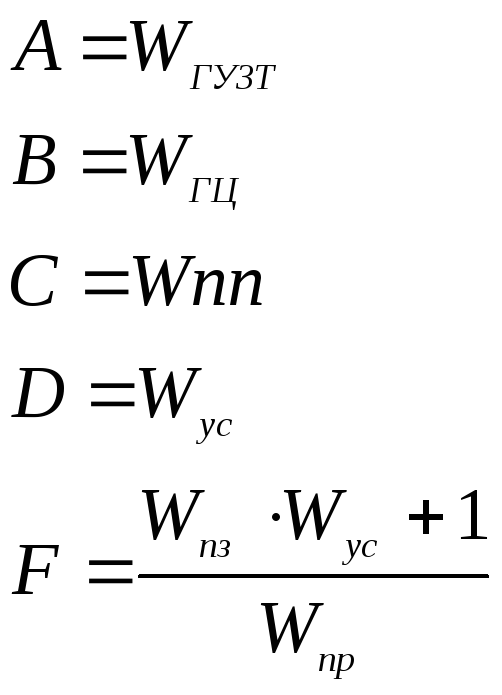
Передаточная функция разомкнутой части системы:
![]()
Передаточная функция замкнутого внутреннего контура системы:
![]()
Общая передаточная функция всей системы имеет вид:
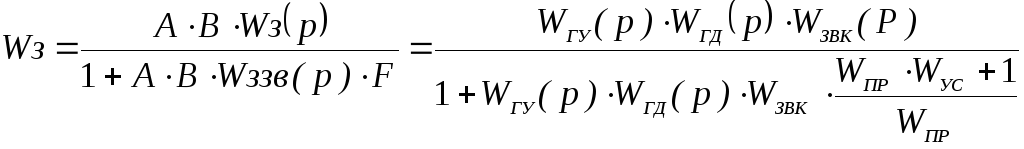
5. Синтез сар
Получили, что передаточная функция разомкнутой части системы имеет вид:
![]()
Вычислим частоту среза и найдем передаточную функцию корректирующего устройства для исследования устойчивости объекта с помощью ЛАХ.

По номограмме Солодовникова определяем диапазон частоты среза в зависимости от заданного времени регулирования, уменьшенного на 30%
![]()
![]()
Строим логарифмическую амплитудную характеристику (прилагается).
Желаемая ЛАХ определяется показателями качества и точностью процесса регулирования. Среднечастотная часть желаемой ЛАХ характеризуется частотой среза. Частота среза определяется с помощью номограммы Солодовника. Для наиболее простой реализации корректирующего устройства последовательные изломы наклонов высокочастотной желаемой ЛАХ и ЛАХ неизменяемой части системы должны совпадать. Строим неизменяемую часть при К неизменяемой части =20·lg22895882750=207; строим желаемую часть при К желаемой =20·lgРу=20lg4785,24=74
Найдем корректирующее устройство. Для нахождения корректирующего устройства необходимо вычесть неизменяю ЛАХ из желаемой Lку=Lж(ω)-Lн(ω)=74-207=-133.
Структурная схема с корректирующим устройством:
Расчет параметров корректирующего устройства
По виду передаточной функции корректирующего устройства определим схему корректирующего устройства.
WКУ=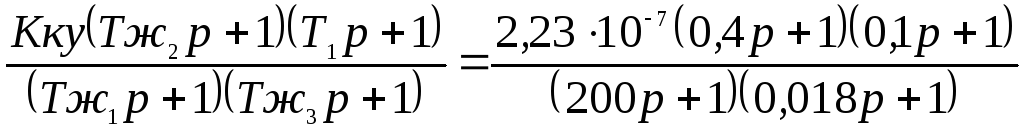
В ыбираем
электрическую схему, передаточную
функцию типового корректирующего
устройства.
ыбираем
электрическую схему, передаточную
функцию типового корректирующего
устройства.
По схеме ККУ=2,23·10-7
W(р)=К
![]()
Примем R1 = 10 Ом
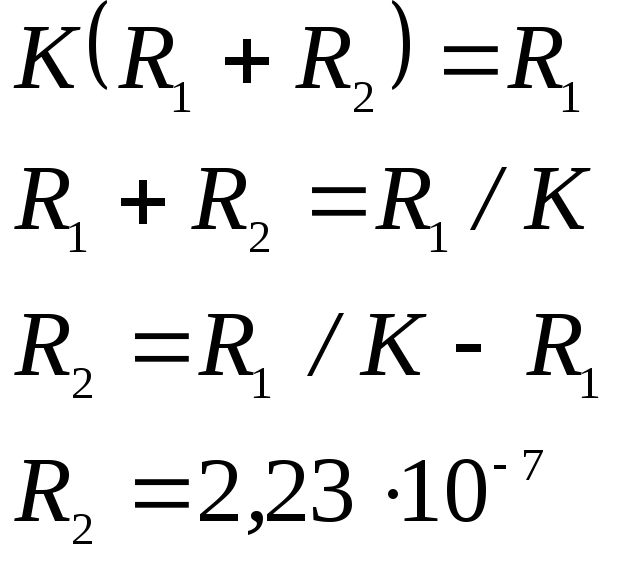
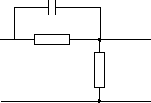
![]()
![]() ;
;
![]()
![]()
Т1=0,4; Т2=200 Т1=0,1; Т2=0,018
![]()
![]()
![]()
![]()
![]()
![]()
К3=![]()
Проверка
![]()
При коррекции с помощью интегрирующих устройств система менее подвержена влиянию помех.
Вывод
В данной курсовой работе произвели анализ исходных данных и из функциональной схемы получили структурную схему САР. Для полученной схемы с помощью пакета Mathlab построили график переходного процесса. Произвели анализ устойчивости некорректированной САР и пришли к выводу , что данная система является устойчивой, а , следовательно , может поддерживать режим работы объекта регулирования при действии на него возмущающих факторов .
Но эта система не соответствует всем необходимым параметрам. Поэтому мы провели синтез САР и подобрали такое корректирующее устройство , при котором система стала отвечать необходимым параметрам. Построили для скорректированной САР графики переходного процесса, АФЧХ. Произвели анализ скорректированной САР и пришли к выводу, что данная САР устойчива и работоспособна.
Данная система соответствует заданным показателям качества:
tp
= 2, с, коэффициент перерегулирования
![]()
