
- •Введение
- •1. Основы моделирования
- •1.1. Математическое моделирование
- •1.2 Математическое моделирование химико-технологических процессов.
- •1.3 Проблемы и перспективы моделирования и проектирования аппаратов химической технологии
- •1.4 Общая схема процесса математического моделирования.
- •1.5 Основные виды математических моделей
- •1.6 Составление математического описания объекта
- •2. Теоретические основы математического моделирования процессов химической технологии.
- •Законы переноса массы, энергии и импульса.
- •2.1 Законы сохранения
- •2.1.1 Закон сохранения энергии
- •2.1.2 Закон сохранения массы
- •2.1.3 Закон сохранения импульса (количества движения)
- •2.2 Законы равновесия
- •2.2.1 Правило фаз
- •2.2.2 Линии равновесия
- •2.3 Законы переноса массы, энергии и импульса
- •2.3.1 Основные механизмы переноса субстанций
- •2.3.2 Основное уравнение переноса субстанций
- •С учетом (25) уравнение (24) примет вид
- •2.3.3 Уравнение переноса теплоты
- •2.3.4 Уравнение переноса массы
- •2.3.5 Уравнения переноса импульса
- •2.3.6 Аналогия процессов переноса
- •2.3.7 Начальные и граничные условия к уравнениям переноса
- •2.3.8 Уравнение переноса в безразмерной форме
- •2.3.9 Моделирование процесса переноса в турбулентном потоке
- •3. Методы моделирования и расчета полимеризационных процессов.
- •3.1 Основные особенности полимеризационных процессов.
3. Методы моделирования и расчета полимеризационных процессов.
В настоящее время математическое моделирование полимеризационных процессов стало весьма популярным. Разработанные методы теоретически позволяют решать задачи, которые совсем недавно казались неразрешимыми. Например, при помощи математического моделирования можно провести на ЭВМ расчет реактора полимеризации любой конфигурации, при любых заданных режимах синтеза и сравнить полученные результаты по производительности, степени превращения и любому параметру качества полимера, поддающемуся количественному выражению исходя из данных о механизме полимеризации и значениях кинетических констант.
В нефтехимической промышленности Татарстана полимеризационные процессы занимают особое место. На таких промышленных гигантах, как ОАО «Нижнекамскнефтехим», ОАО «Оргсинтез», Казанский завод синтетического каучука процессы полимеризации составляют основу производства. Применение математического моделирования позволяет оптимизировать режимы работы полимеризационных аппаратов и улучшать качество получаемых полимеров.
3.1 Основные особенности полимеризационных процессов.
Высокомолекулярные соединения - это вещества, молекулы которых состоят из большого числа повторяющихся звеньев, связанных между собой химическими связями. Схематически такая молекула может быть представлена в виде:
~А—А—А—А—А~ или (—А—)п,
Вследствие высокой молекулярной массы и значительной протяженности таких молекул их обычно называют макромолекулами или полимерными цепями.
Величина п может меняться в широких пределах, и макромолекулы, построенные из одинаковых звеньев, но различающиеся их числом, являются представителями одного гомологического ряда (полимергомологи). Если проследить изменения какого-либо физического свойства вещества f от величины п, то можно выделить три характерные области (рис.):
I - область низкомолекулярных веществ, когда рассматриваемый показатель практически пропорционален молекулярной массе;
III - область высокомолекулярных соединений, когда даже заметное повышение числа звеньев почти не влияет на свойства;
II - переходная область, когда и происходит постепенное уменьшение влияния молекулярной массы на свойство.
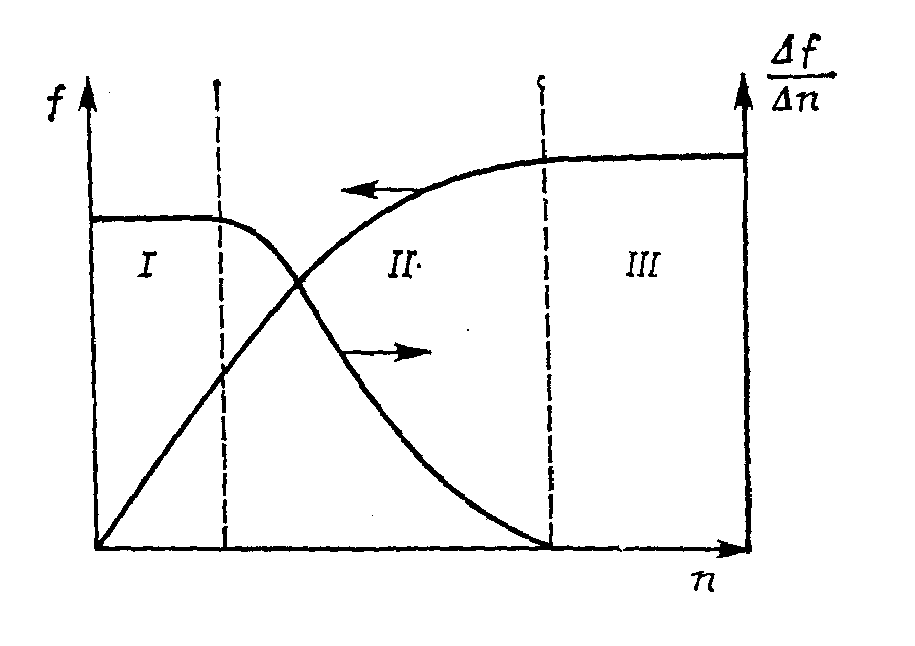
Рис.1 Схема влияния длины цепи на свойства веществ: I – низкомолекулярные вещества; II – олигомеры; III – высокомолекулярные соединения.
Полимергомологи
переходной области получили название
олигомеров, они не проявляют
еще всех свойств, характерных для
полимеров, но уже не могут быть разделены
на индивидуальные соединения, подобно
низкомолекулярным веществам. Хотя
количественное накопление числа звеньев
в цепи приводит к качественному изменению
свойств материала, переходы низкомолекулярное
вещество - олигомер – полимер - являются
довольно размытыми. Верхний предел
молекулярных масс олигомеров существенно
зависит от их химической природы,
составляя около
![]() для неполярных и
для неполярных и
![]() для полярных полимергомологов.
для полярных полимергомологов.
Вследствие статического характера большинства процессов образования макромолекул практически все высокомолекулярные соединения состоят из полимерных цепей с различной молекулярной массой, т.е. являются веществами полидисперсными, или полимолекулярными. Поэтому такая важная характеристика полимера как молекулярная масса всегда является величиной усредненной.
Полимеры, обладая одинаковой средней молекулярной массой, могут существенно различаться по полидисперсности, и для количественного описания вклада макромолекул различной длины в суммарное значение М необходима следующая важнейшая характеристика - функция молекулярно-массового распределения (ММР). Чем сильнее различаются по молекулярной массе отдельные макромолекулы полимера, т.е. чем выше его полидисперсность, тем шире молекулярно-массовое распределение.
Существует несколько способов усреднения молекулярной массы полимеров, и в зависимости от способа усреднения различают среднечисленную Мп, среднемассовую МW, и так называемую z-среднюю или среднеседиментационную МZ молекулярную массу. Среднечисленная молекулярная масса получается при усреднении по числу макромолекул каждой молекулярной массы. Среднемассовая молекулярная масса получается при усреднении по массе макромолекул каждого типа.
Характерной особенностью процесса синтеза полимеров является неоднозначность молекулярной структуры продуктов полимеризации, а следовательно, и их физико-механических свойств. Даже при условии идеального ведения процесса (постоянство температуры, отсутствие градиента концентраций, равномерность подачи катализатора и т.д.) невозможно получить полимер со строго фиксированной молекулярной структурой. Естественно, разброс становится еще большим, если имеются какие-либо отклонения от идеальности.
Неоднородность линейных гомополимеров обусловлена различной молекулярной массой, несимметричностью расположения разных групп-заместителей в мономерных звеньях. Для сополимеров к этим характеристикам добавляются частота чередования различных мономерных блоков и их размер. Разветвленные полимерные молекулы характеризуются дополнительно числом и функциональностью точек ветвления и размерами ветвей. В сетчатых полимерах имеются циклы из мономерных звеньев, настолько усложняющие и запутывающие их структуру, что до настоящего времени не придумано удовлетворительного способа их описания.
Поэтому, если при расчете и оптимизации процессов с низкомолекулярными соединениями параметрами являются только количественные характеристики (например, производительность аппаратов, экономичность их работы, чистота и себестоимость продукции), то при моделировании полимеризационных процессов необходимо учитывать структуру, а, следовательно, качество получаемого продукта.
Таким образом, при моделировании и расчете полимеризационных процессов возникают существенные трудности. Это, во-первых, необходимость выбора структурных параметров, в той или иной степени полно отражающих свойства материала, с одной стороны, и вычислимых из кинетической схемы если не аналитически (такая возможность по мере углубленного изучения полимеризационных процессов становится все более и более редкой), то хотя бы на реальных ЭВМ, с другой стороны. Во-вторых, это наличие практически бесконечного набора компонентов синтеза, а, следовательно, необходимость решения бесконечных систем уравнений. И, наконец, в-третьих, часто присущие полимеризационным процессам большие значения вязкости, что значительно усложняет их кинетику, а, следовательно, и расчет соответствующих моделей.
Пожалуй, наиболее
четкой и установившейся функцией
структуры, достаточно полно характеризующей
свойства, во всяком случае линейных
гомополимеров является молекулярно-массовое
распределение (ММР), значения которого
W(![]() )
пропорциональны общей массе полимерных
молекул, содержащих n
мономерных звеньев. В эквивалентной
непрерывной форме ММР - это функция
W(
),
описывающая молекулярную массу полимерных
молекул, число звеньев в которых
колеблется в пределах от
до
+d
,
и пропорциональная W(
)d
.
Если R(
)
- концентрация (или число) полимерных
молекул длины
,
то
)
пропорциональны общей массе полимерных
молекул, содержащих n
мономерных звеньев. В эквивалентной
непрерывной форме ММР - это функция
W(
),
описывающая молекулярную массу полимерных
молекул, число звеньев в которых
колеблется в пределах от
до
+d
,
и пропорциональная W(
)d
.
Если R(
)
- концентрация (или число) полимерных
молекул длины
,
то
![]() ,
(1)
,
(1)
Функцию R( ) часто называют молекулярно-числовым распределением. Формула (1) устанавливает их эквивалентность.
Важными параметрами молекулярно-массового (молекулярно-числового) распределения являются его моменты:
![]() , (2)
, (2)
Через них вычисляются следующие наиболее употребительные в полимерной химии характеристики:
среднечисленная степень полимеризации
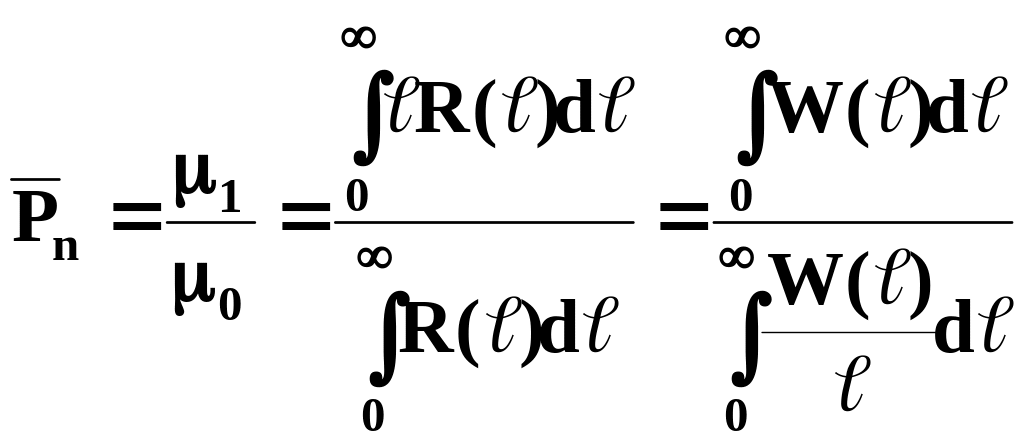 , (3)
, (3)
(средняя длина полимерных молекул);
среднемассовая степень полимеризации
![]() , (4)
, (4)
(средняя молекулярная масса полимера);
среднеседиментационная степень полимеризации
![]() , (5)
, (5)
дисперсия молекулярно-числового распределения
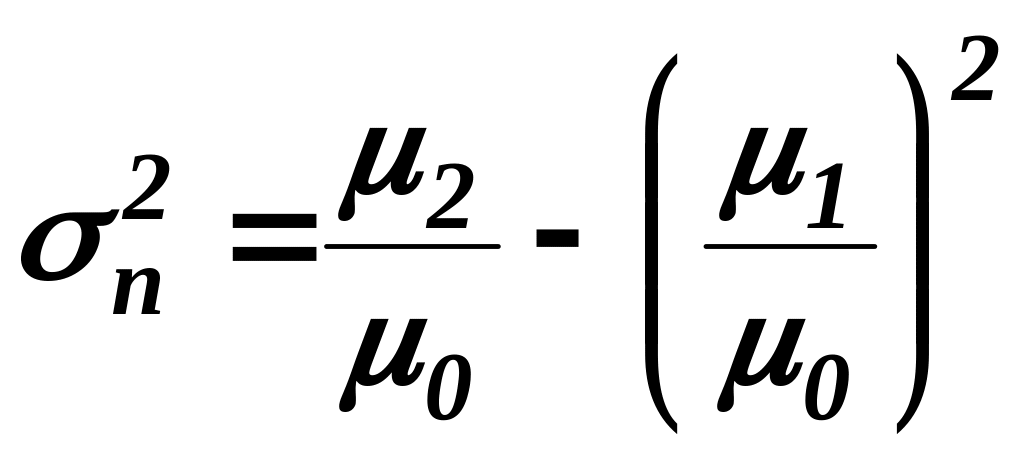 , (6)
, (6)
дисперсия молекулярно-массового распределения
 , (7)
, (7)
ширина ММР
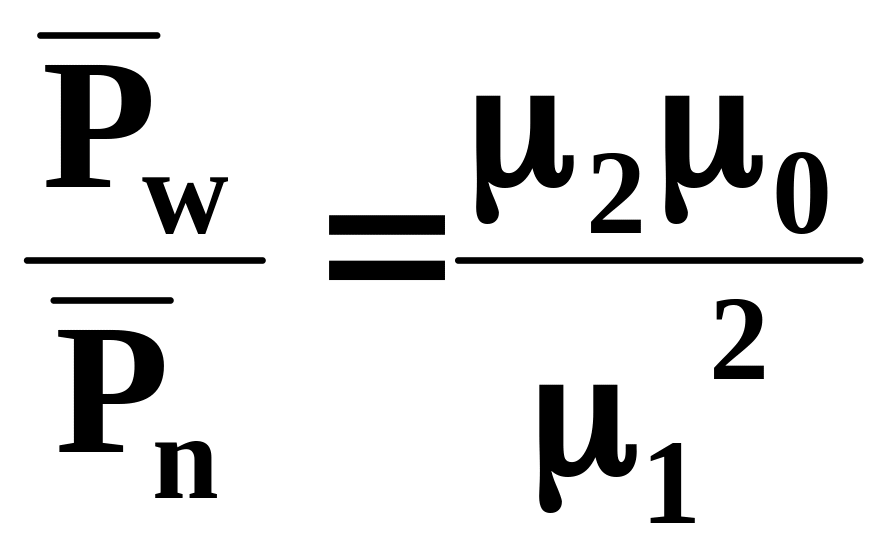 . (8)
. (8)
Одной из важных характеристик молекулярной структуры полимера, состоящего из и различных типов мономерных звеньев является молекулярно - числовое распределение N( 1, 2,…, k), зависящее от k натуральных аргументов, значения которого пропорциональны концентрациям (числу) полимерных молекул с 1 звеньями одного мономера, 2 звеньями другого, ..., k звеньями k-того. Соответствующее ММР можно получить при помощи следующей формулы:
![]() ,
,
где m1, m2, ..., mk - молекулярные массы соответствующих мономерных звеньев.
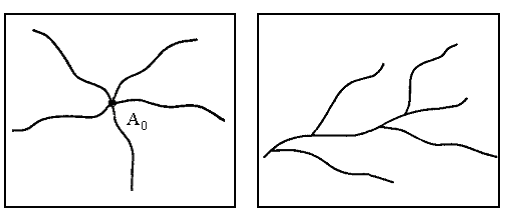
Задача же удовлетворительного описания молекулярной структуры разветвленных и, особенно, сетчатых полимеров чрезвычайно сложна и вплоть до настоящего времени не решена. Исключение составляют, пожалуй, лишь два типа разветвлений. Это - «звездчатые» полимеры (рис.2), в которых
|
Рис.2
«Звездчатый» тип разветвления полимеров.
|
Рис.3 Разветвленная
макромолекула (разветвления на
основной линейной цепи).
Первый тип полимеров может быть в достаточной степени полно описан k - мерной вектор - функцией молекулярно-числовых распределений:
Описание разветвленных молекул второго типа эквивалентно описанию линейного бинарного сополимера, в котором роль мономерных звеньев одного типа играют звенья из основной линейной цепи, а другого - звенья из боковых цепей. Другим не менее важным этапом, без которого бессмысленно дальнейшее построение модели, является выявление корреляции между введенными структурными характеристиками и свойствами материала.
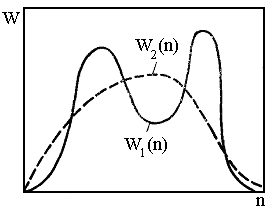
W2(
)
W1(
) Рис.4 Молекулярно-массовые распределения разной формы с одинаковыми первыми моментами. В
полимерной технологии очень часто, к
сожалению, ограничиваются единственным
параметром структуры - одной из средних
молекулярных масс. Этого явно
недостаточно даже для линейных
гомополимеров, поскольку очень сильное
влияние на свойства материала оказывает
форма ММР, в частности, его ширина. Эти
два параметра, конечно, тоже не
характеризуют полностью ММР, а,
следовательно, и свойства полимера.
Например, исходя из значения только
этих параметров, нельзя уловить эффекта
полимодальности ММР. Так, полимеры с
ММР W1(
)
и W2(
)
(рис.4) имеют одинаковые значения
Однако имеются практически важные случаи, когда свойства полимера достаточно хорошо описываются указанными двумя параметрами. Для таких процессов кривые молекулярно-массового распределения имеют некий регулярный характер и поэтому не безнадежным являются попытки восстановления полных кривых ММР по конечному набору его моментов. Бемфорд и Томпа предложили пользоваться для этой цели полиномами Лагерра. Разработанные в настоящее время математические методы моделирования и расчета полимеризационных процессов можно условно разделить на четыре группы: эмпирические, кинетические, статистические или случайные (Монте-Карловские) методы машинного моделирования. Условность такого разделения заключается, во-первых, в том, что между перечисленными группами методов не существует четких границ и, во-вторых, в том, что удовлетворительное описание большинства реальных процессов требует целого комплекса методов из разных групп. Остановимся подробнее на каждой из них.
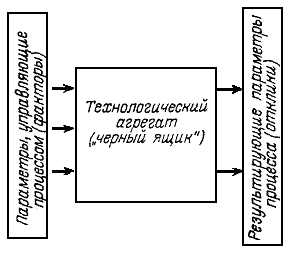
3.2 Эмпирические методы расчета реакторов - полимеризаторов. Это - наиболее часто используемые в полимерной технологии методы расчета промышленных реакторов. Они основаны на знании некоторых экспериментальных кинетических и структурных закономерностей протекания процесса, полученных без выявления детальной кинетики, справедливых обычно в очень узком интервале условий синтеза. Для сложного и недостаточно изученного процесса эмпирические методы оказываются применимыми, однако, к сожалению, они часто используются в технологии и в тех случаях, когда существует более тонкое описание процесса, позволяющее вести его экономичнее и получать при этом продукт более высокого качества. В настоящее время разработан мощный математический аппарат планирования эксперимента, так называемые методы черного ящика, позволяющие рассчитывать процесс и управлять его работой даже в том случае, когда нет никаких данных ни по химии процесса, ни по тепловому и гидродинамическому режимам работы аппаратов. Сущность этих методов состоит в статистическом построении вероятных полиноминальных зависимостей выходных данных процесса (откликов) от управляющих параметров (факторов) на основе имеющегося небольшого набора данных по измерению этих величин (рис.5).
Рис.5 Схема эмпирической модели процесса. Безусловно, нет смысла отказываться от таких методов моделирования, если соответствующие процессы уже существуют в промышленности, однако, нет никакой надежды на их существующую интенсификацию и оптимизацию свойств продукта без детального изучения кинетических, структурных и других закономерностей. Методы планирования эксперимента не дают возможности экстраполяции полученных закономерностей на другие условия, а, следовательно, исключают возможность коренного усовершенствования процесса.
3.3 Кинетические методы моделирования Кинетика изучает скорость и механизмы химических реакций. Кинетики работают на два фронта. С одной стороны, они пытаются проанализировать механизмы сложных реакций, разделить их на стадии, чтобы установить их последовательность и влияние друг на друга. Здесь они соприкасаются с интересами химиков-синтетиков. С другой стороны, кинетики могут рассчитать, как вести химические процессы в промышленности, чтобы повысить скорости реакций, увеличить выход продуктов, получить материалы с требуемой структурой. Здесь скрещиваются интересы химиков и технологов. Значит, кинетика – как бы, связывающее звено, которое объединяет химию и технологию. Химик мыслит качественно, пишет уравнения реакций, которые собирается осуществить, рассуждает об активности веществ. Если он подозревает существование примесей или промежуточных продуктов, то никогда не поверит в них, пока не увидит собственными глазами – видит или установит специальным анализом. Технолог мыслит материальными и тепловыми балансами, кубометрами и тоннами, технологическими схемами, насосами, мешалками, электромоторами. Частенько он не столь уж хорошо разбирается в механизме реакции, протекающей у него в аппарате, но сколько и чего подается в аппарат и сколько выгружается – это он знает отлично. Кинетика насыщена математикой. Свои закономерности она излагает на языке дифференциальных и интегральных уравнений. Расчет кинетики процесса с участием макромолекул полимера заключается в установлении зависимости скорости протекания процессов и статистических характеристик полимеров от значений констант элементарных реакций, концентраций реагентов и способа их введения в зону реакции. Кинетический подход заключается в составлении и решении кинетических уравнений для концентрации всех типов молекул, радикалов или других активных частиц, участвующих в процессе. Эти уравнения выводятся из условий математического баланса по каждому компоненту реакции с учетом закона действующих масс, определяющего скорость образования этого компонента Число моделей на этом уровне особенно велико. Теоретические модели состоятся исходя из некоторого механизма протекания процесса. Число реагирующих компонентов в полимеризационной системе бесконечно, следовательно, и число соответствующих кинетических уравнений и констант скоростей элементарных реакций бесконечно. Получаемая бесконечная цепочка дифференциальных уравнений может решаться различно. Прямые численные методы решения таких систем даже при применении быстродействующих машин недостаточно эффективны. Таким образом, при математическом моделировании кинетики процессов полимеризации на уровне описания ММР последовательно решаются две задачи: 1) сведение бесконечной системы дифференциальных уравнений, записанных относительно концентраций полимерных молекул, к конечной системе уравнений относительно моментов распределения концентраций полимерных молекул по их признакам; 2) получение выражений для расчета этих распределений. При анализе полимеров важно знать степень полимеризации макромолекул или молекулярную массу. При фракционировании полимеров получают кривые распределения. При построении кривых массового распределения следует учитывать, что каждая фракция содержит макромолекулы не одинакового размера, а узкий набор размеров, ограниченный определенным интервалом. Для получения дифференциальной кривой массового распределения строят график в координатах: на оси абсцисс откладывают длину полимерной цепи (размер), а на оси ординат – массовую долю макромолекул с данной молекулярной массой, деленную на интервал молекулярных масс. Площадь под кривой будет равна числу всех макромолекул в образце. Аналогичную кривую можно построить, если на оси ординат откладывать числовые доли макромолекул, отнесенные к определенному интервалу размеров. Такая кривая называется дифференциальной кривой числового распределения. Для количественного сравнения удобно пользоваться понятием средних величин: среднечисленная и среднемассовая молекулярные массы. Остановимся подробнее на некоторых наиболее распространенных методах кинетического моделирования полимеризационных процессов.
Непосредственное интегрирование кинетической схемы Возможность получения аналитических выражений для расчета концентраций и молекулярно-массовых распределений чрезвычайно заманчива, но, к сожалению, встречается очень редко. Возможность аналитического интегрирования кинетической схемы определяется следующими условиями: 1. Кинетические уравнения рекуррентны. Выполнение этого условия означает отсутствие в кинетическом механизме реакций деструкции. 2. Каждое кинетическое уравнение интегрируется в квадратурах, если все предыдущие проинтегрированы.
3.
Формулы, выражающие зависимость
Это условие почти никогда не выполняется. Даже в простейшем случае нельзя проинтегрировать таким способом кинетическую схему, если не выполняется принцип Флори о независимости кинетических констант полимеризации от длины цепи. Перечисленные условия являются настолько жесткими, что для подавляющего большинства реальных механизмов непосредственное интегрирование кинетических уравнений невозможно. Однако часто аналитические методы в совокупности с методами численного интегрирования на ЭВМ оказываются чрезвычайно полезными для априорного анализа искомых зависимостей, для выявления вида молекулярно-массовых распределений.
Метод моментов Статистические моменты могут быть вычислены по известному распределению, однако, существует и другой способ расчета величин (метод моментов), позволяющий в некоторых случаях обойтись без знания явного вида функции распределения. Этот способ заключается в выводе из кинетических уравнений и решении цепочки дифференциальных уравнений непосредственно для искомых статистических моментов. Рассмотрим в качестве примера механизм по типу «живой» полимеризации с мгновенным инициированием, осложненной реакцией передачи цепи на мономер
где
Начальные
условия для моментов
при i=0 имеет вид:
а при i=1:
При переходе к конверсионной зависимости уравнение для мертвых цепей примет вид:
Введем
параметр
а уравнение для живых цепей примет вид
Моменты молекулярно-массового распределения:
По определению
Опираясь на определение моментов уравнения (13), (14)записываем относительно нулевых, первых и вторых моментов молекулярно-массового распределения
Преобразования
дают:
Метод производящих функций Пусть имеется некоторая переменная , которая принимает любое значение из набора целых положительных чисел (например, число звеньев в цепи макромолекулы). Тогда произвольному распределению R( ) этой переменной может быть поставлена в соответствие производящая функция g(s) по следующей формуле
Переменная s, являющаяся аргументом производящей функции, носит чисто вспомогательный характер и не относится ни к какой реальной физической либо химической величине. Если распределение зависит от времени или каких-либо других параметров, то от них будет также зависеть функция g. Статистические моменты (k) любого k-ого порядка распределения R( ) могут быть просто выражены через производные этого же порядка от функции g в точке s=1
Если переменная принимает не дискретный, а непрерывный набор возможных значений, то в качестве аналога формулы можно выбрать соотношение
определяющее производящую функцию как преобразование Лапласа от распределения R( ). В некоторых случаях бывает необходимо описать распределение в зависимости от нескольких переменных, которые имеют как непрерывный, так и дискретный характер, тогда производящая функция значительно усложняется:
где, например, i – количество активных центров на макромолекуле, j – количество разветвлений на макромолекулу, - количество звеньев в макромолекуле. Метод введения непрерывной длины цепи Для
высокомолекулярного полимера ( Метод производящей функции позволяет рассчитывать молекулярные распределения лишь в аналитически интегрируемых случаях и, поскольку моделирование большинства реальных полимеризационных процессов требует применения численных методов. Расчет молекулярных распределений во многих процессах радикальной, ионной и координационной полимеризации становится возможным вследствие совместного использования метода производящей функции и метода введения непрерывной длины цепи. Пример: Рассмотрим в качестве примера механизм по типу «живой» полимеризации с мгновенным инициированием, осложненной реакцией передачи цепи на мономер и полимер
где концентрация макромолекул с i активными центрами и мономерными звеньями в момент времени t (при этом «мертвым» цепям соответствует i=0 (отсутствие активного центра на макромолекуле)), I – концентрация инициатора, M – концентрация мономера.
Для решения уравнения (11) введем производящую функцию
Система уравнений, описывающих процесс полимеризации, в итоге будет сведена уравнению относительно производящей функции:
Произвольный статистический момент ММР k связан с F соотношением
При
введении обозначения:
Для нахождения производных более высокого порядка достаточно дифференцировать соответственно по s и p необходимое число раз уравнение для производящей функции.
Начальные
условия при x=0:
Полученная система дифференциальных уравнений относительно моментов молекулярно-массового распределения решается с помощью численных методов.
3.4 Статистические методы расчета молекулярных распределений полимеров Статистические методы моделирования полимеризации состоят в рассмотрении образования полимерной молекулы как некоторого случайного процесса с теми или иными вероятностями различных реакций. В настоящее время разработан мощный аппарат теории вероятности и математической статистики, поэтому развитие статистических методов моделирования полимеризации является, безусловно, перспективным. Кинетические уравнения, лежащие в основе группы кинетических методов моделирования, выводятся на основе сравнения вероятностей реализации различных элементарных стадий рассматриваемого процесса, поэтому формально кинетические методы могут быть включены в группу статистических, однако этого не следует делать по следующим соображениям. Во-первых, потому, что в кинетических методах вероятностные соображения нужны лишь при выводе кинетических уравнений, в статистических же методы теории вероятности используются на всех стадиях моделирования. Во-вторых, потому, что кинетические модели оперируют с макросовокупностью молекул, статистические - с индивидуальной полимерной молекулой.
Последовательность
случайных событий с конечным числом
исходов на каждом шаге называют
марковским случайным процессом, если
вероятности событий на k-том
шаге зависят только от состояния
системы на предыдущем, (k
- 1) шаге. Марковский процесс полностью
определяется матрицей
где Рk - матрица P в степени k. Заметим, что статистические методы могут оказаться чрезвычайно полезными при идентификации молекулярных распределений, характеризующих структуру полимеров. Однако при моделировании реальных технологических процессов необходимо дополнительное привлечение кинетических или брутто-кинетических методов, без которых невозможно вычисление количественных характеристик работы реакторов (конверсии, производительности). Моделирование полимеризационных процессов на ЭВМ методами Монте-Карло. Эта группа методов применяется в тех случаях, когда кинетический механизм настолько сложен, что не поддается ни кинетическому, ни статистическому моделированию. Он состоит в прямом моделировании на ЭВМ случайного процесса образования полимеров. Этот метод, с одной стороны, универсален, поскольку можно в принципе рассчитать модель любого кинетического механизма, с другой стороны, применение его сильно ограничено возможностями (быстродействием, памятью) существующих в настоящее время ЭВМ. Его нельзя, применять в технологических расчетах и автоматизированных системах управления, но он может оказаться очень полезным при фундаментальных исследованиях: проверке адекватности предложенного механизма, выяснении вида молекулярно-массового распределения, оценки влияния на ход процесса соотношений между кинетическими константами и т. д. Метод этот заключается в следующем. В память машины вводится исходная информация: механизм процесса, значения кинетических констант, число свободных мономерных звеньев, число частиц инициатора, исходный набор различных полимерных цепей, количество мономера и т.д. После этого машина начинает моделировать процесс, выбирая из всех возможных стадий одну в соответствии с их вероятностями.
4. Математическое моделирование совмещенных процессов массопереноса с химической реакцией. В последнее время наблюдается мировая тенденция использования химической технологии в совмещенных процессах, в которых химическое превращение веществ осуществляется совместно с целенаправленным разделением реакционной смеси в одном и том же аппарате. К таким процессам относятся реакционно-абсорбсорбционные, реакционно-экстракционные, а также процессы, в которых химическое превращение успешно сочетается с ректификацией или отгонкой. Известны реакционно-осмотические, реакционно-отделительные процессы и многие другие случаи направленного совмещения. В любом из перечисленных процессов химическая реакция составляет единую сложную систему с массопереносом.
Рассмотрим
в качестве примера обратимую реакцию
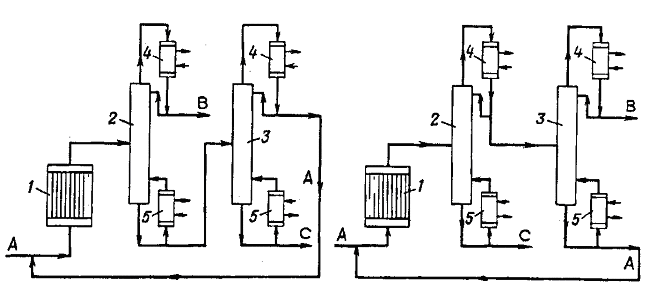
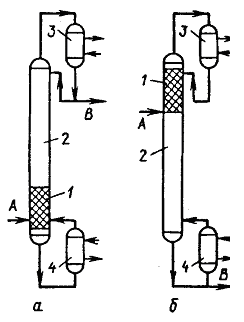
Рис. 1 Альтернативные варианты технологической схемы, основанные на принципе раздельного проведения химической реакции и выделения целевых продуктов: 1 - реактор; 2,3 - ректификационные колонны; 4 - конденсатор; 5 – кипятильник. На рис. 2 приведена ректификационная колонна, действующая на основе принципа направленного совмещения реакционного и ректификационного процессов. Так как компонент А является среднелетучим, его концентрация будет максимальна в середине ректификационной колонны. Именно в этой зоне и размещается специально подобранный катализатор, который одновременно выполняет роль насадки. В качестве дистиллята отбирается практически чистый компонент В, а из нижней части колонны - компонент С. Питанием служит чистый компонент А. Концентрация компонента В, как самого легколетучего, максимальна в дистилляте. При достаточной эффективности колонны, а также соответствующей производительности реакционной зоны можно получить в дистилляте практически чистый компонент В, а в продукте, отбираемом с нижней тарелки, - практически чистый компонент С. По сравнению с ранее рассмотренными схемами здесь исключается внешний рецикл и сокращается число аппаратов, сокращаются также и энергетические расходы. Особенно большой эффект достигается при использовании специально приготовленных в том числе и формованных катализаторов, которые способны обеспечить надлежащие гидродинамические условия в аппарате.
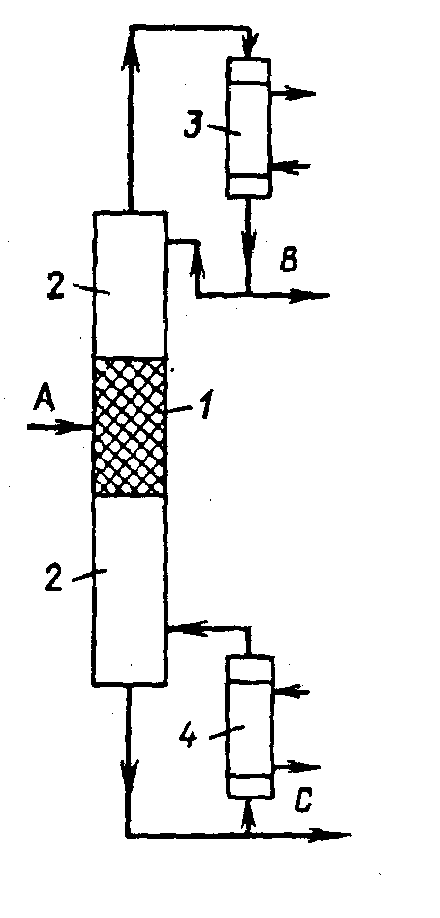
Рис. 2 Реакционно-ректификационный аппарат: 1 - реакционная зона; 2 - ректификационная зона; 3 - конденсатор; 4 - кипятильник. Этот простой пример хорошо иллюстрирует преимущества совмещённых процессов. В общем случае совмещенные процессы позволяют в корне изменить технологию получения того или иного продукта и предоставляют новые возможности в организации технологических процессов. Без преувеличения можно сказать, что максимальное использование этих возможностей является одной из современных задач химиков-технологов на пути создания энергосберегающих, экологически чистых технологий.
4.1 Области использования совмещенных процессов Совмещенные процессы могут с успехом использоваться в любой отрасли химического производства. Целенаправленное или интуитивное использование реакционно-ректификационных, реакционно-отгонных и других типов совмещенных процессов особенно распространено в отрасли основного органического и нефтехимического синтеза, в которой совмещенные процессы используются в следующих случаях: 1. В жидкофазных процессах, когда тепло, выделяемое при протекании экзотермических реакций, отводится за счет испарения реакционной смеси, которое сопровождается ее частичным разделением. 2. При протекании двухсторонних химических превращений с целью «обхода химического равновесия», т. е. увеличения конверсии по сравнению с химически равновесной вследствие избирательного непрерывного отвода из реакционной зоны посредством массообмена образующихся продуктов. 3. Для химических превращений произвольного типа, когда интенсивный отвод продуктов за счет целенаправленного использования массообменных процессов в общем случае способствует уменьшению доли побочных реакций и, как следствие, увеличению селективности процесса. При этом одновременно создаются более благоприятные условия для осуществления целевой реакции - возрастает концентрация реагентов в реакционной зоне и уменьшается время пребывания в ней целевых продуктов. 4. Для разделения близкокипящих продуктов или азеотропных смесей, когда разделяемые компоненты в условиях разделения реагируют с некоторым дополнительно вводимым либо изначально присутствующим в системе веществом, а образующийся при этом продукт легко может быть выделен из многокомпонентной смеси.
4.2 Признаки совмещенного процесса.
Таким образом, под непрерывным совмещенным реакционно-массообменным процессом понимается такой процесс, при котором химическое превращение сопровождается одновременным (в рамках одного аппарата) разделением реакционной смеси посредством избирательного обмена продуктами реакции между реакционной зоной и окружающей средой. Теперь мы можем уточнить определение совмещенного процесса. Под непрерывным совмещенным процессом понимается сложный процесс, в котором совместно в рамках одного аппарата протекают по крайней мере два процесса, один из которых выполняет роль источника (стока) вещества и обеспечивает конверсию, а другой обеспечивает селективность, выполняя роль избирательного стока (источника) вещества внутри системы или избирательный обмен веществом с окружающей средой. Результатом совмещения является преодоление термодинамических ограничении, свойственных каждому сопряженному процессу, взятому в отдельности.
4.3 Основные преимущества совмещенных процессов. 1) Экономия энергии за счет ликвидации промежуточных стадий перекачки и подогрева; 2) Снижение металлоемкости аппаратов; 3) Снижение себестоимости эксплуатации оборудования (например, уменьшение налогов и объема освидетельствования); 4) Улучшение селективности и конверсии процесса. Рассмотрев основные признаки совмещенных процессов, можно сделать вывод о том, что совмещенный процесс не является аддитивным объединением составляющих его процессов. При совмещении появляются новые возможности, которые позволяют преодолеть ограничения, свойственные каждому процессу в отдельности. Степень преодоления этих ограничений и характеризует случай, когда совмещенный процесс будет обладать явными преимуществами по сравнению с другими формами организации. При этом наибольшими преимуществами будет обладать такой совмещенный процесс, в котором одновременно преодолеваются термодинамические ограничения по обеим составляющим.
Рассмотрим
двухстороннюю химическую реакцию
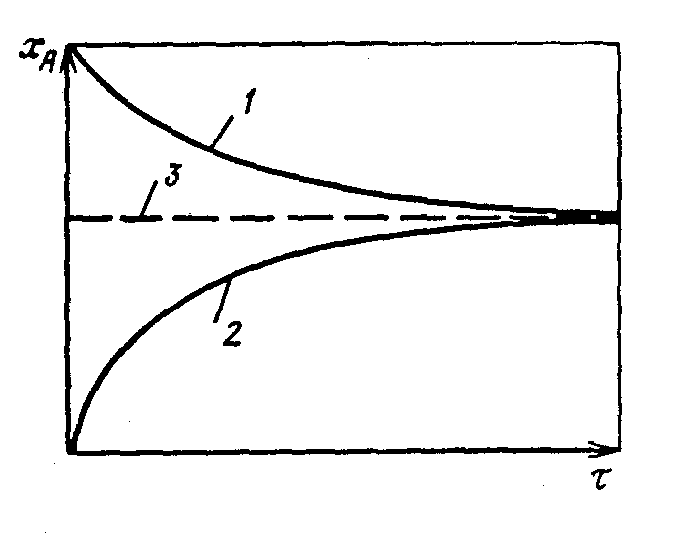
Рис. 8 Типичные кинетические кривые: 1 - прямая реакция; 2 - обратная реакция; 3 - равновесный состав.
По
мере асимптотического приближения
кинетической кривой к горизонтальной
прямой, характеризующей равновесный
состав, скорость обратной реакции
будет уменьшаться. В пределе, если
время
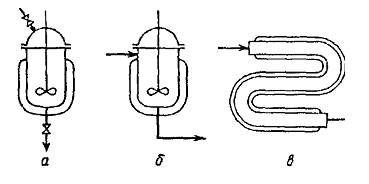
Очевидно, что если технологически оформить рассматриваемый жидкофазный процесс, выбрав реактор периодического действия с мешалкой и внешним теплообменом с окружающей средой, то в зависимости от времени работы этого реактора мы в лучшем случае получим состав, в той или иной степени приближающийся к равновесному. При значительном увеличении продолжительности процесса будут развиваться и побочные реакции различного типа, что нежелательно. Реактор периодического действия можно заменить на проточный реактор, например реактор полного смешения или реактор полного вытеснения. Однако такой переход к проточным открытым системам приведет в конечном итоге к составам, еще более удаленным от равновесных, так как время пребывания реакционной смеси в таких реакторах конечно. Таким образом, при проведении процесса в любом из реакторов, изображенных на рис. 3, в качестве конечного результата будет получен некоторый состав реакционной смеси, лежащий в области протекания прямой реакции, где термодинамическим ограничением по химической составляющей является химическое равновесие.
Рис. 3 Типы реакторов: а - реактор периодического действия; б - проточный реактор полного смешения; в - проточный реактор полного вытеснения.
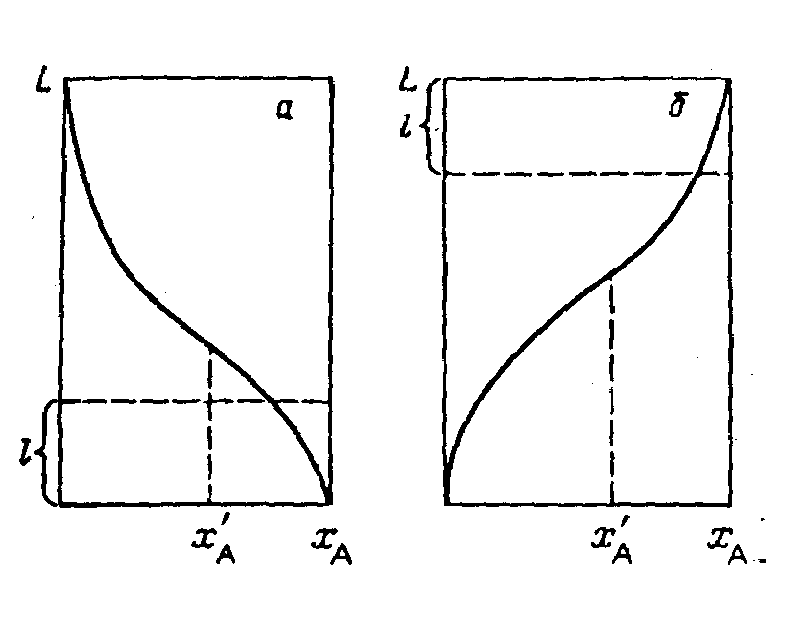
Рис. 4 Варианты непрерывного реакционно-ректификационного процесса: 1 - реакционная зона; 2 - ректификационная зона; 3 - конденсатор; 4 - кипятильник; А - исходное вещество; В - продукт реакции. Ситуация изменится, если технологическое оформление процесса осуществить по принципу совмещения. Допустим, мы остановились на реакционно-ректификационном процессе. Если легколетучим компонентом является компонент В, то процесс может быть осуществлен в ректификационной колонне непрерывного действия, в которой каталитическая зона расположена в нижней части колонны. В качестве дистиллята выводится практически чистый компонент В, а кубовый продукт не отбирается. Распределение компонентов по высоте аппарата будет иметь вид, представленный на рис. 4а. В случае азеотропной смеси наверху колонны концентрация компонента А XА 0, в кубе колонны - XА 1. Компонент В будет иметь концентрацию XВ 1 наверху колонны и XВ 0 в кубе колонны. Таким образом, при размещении каталитической зоны в нижней части колонны химическая реакция будет протекать в области, где ее скорость является наивысшей (В 0). Результатом такого процесса будет получение чистого компонента В в виде дистиллята. Теперь допустим, что легколетучим компонентом будет компонент А. В этом случае отбор практически чистого компонента В можно организовать в виде кубового продукта, осуществив режим полного орошения в колонне, т. е. замкнув верхний отбор. Каталитическую зону в этом случае необходимо разместить в верхней части колонны (рис. 4б). Распределение компонента В по высоте колонны представлено на рис. 4б. Эффект, полученный в случае совмещенного процесса, часто объясняют «смещением равновесия». На самом деле состояние химического равновесия зависит только от температуры и давления. Так как средние температуры во всех рассмотренных случаях одинаковы, получаемый в совмещенном процессе конечный результат обусловлен не смещением равновесия, а эффективностью массообменного процесса, в результате которого происходит избирательный вывод в практически чистом виде продукта реакции (компонента В) с одновременным концентрированием реагента А в зоне реакции. Это и позволяет получить выход продукта В, превышающий предельно допустимый в закрытых или простых проточных системах (см. рис. 2).
Рис. 5 Распределение компонентов А и В по высоте аппарата: а - легколетучим является компонент В; б - легколетучим является компонент А; L - высота колонны, l - высота реакционной зоны; х'А - равновесный химический состав. Вторая возможность, появляющаяся при осуществлении совмещенных процессов, связана с увеличением селективности в случае протекания сложных реакций. Эта возможность обусловлена, прежде всего, тем, что, подобрав соответствующие условия проведения совмещенного процесса и расположение реакционной зоны, всегда можно организовать процесс таким образом, чтобы его протекание описывалось бы только начальным участком кинетической кривой для стационарного режима. Именно на этом участке селективность процесса будет наивысшая, наивысшей будет и скорость химической реакции. Использование совмещенных процессов позволяет также обеспечить высокую движущую силу процессов за счет естественного противотока реагентов и перераспределения компонентов вдоль аппарата. Эта возможность обеспечивается оптимальным размещением зоны реакции и концентрационным перераспределением компонентов в колонном противоточном аппарате. В ряде случаев переход к совмещенным процессам позволяет создать «мягкие» условия подвода и отвода тепла. Кроме этого, совмещение позволяет упростить организацию непрерывных процессов, что является немаловажным фактором, особенно в крупнотоннажных производствах, например в производствах основного органического синтеза. И, наконец, использование совмещенных процессов позволяет сделать более компактными технологические схемы и тем самым сократить капитальные затраты. Выше были перечислены только главные преимущества совмещенных процессов. Естественно, полнота реализации этих преимуществ будет зависеть в каждом конкретном случае от химических и физико-химических свойств, как чистых компонентов, так и их смесей. В целом, преимущества совмещенных процессов играют особую роль в свете разработки безотходной и малоотходной технологий получения различных продуктов органического синтеза. Здесь особое значение приобретают увеличение селективности процессов и увеличение степени превращения реагентов за один проход. Первое приводит к снижению количества побочных продуктов, что в свою очередь позволяет полностью или частично решить проблему их утилизации или уничтожения. Второе создает необходимые условия для снижения числа рециклов реагентов. В идеальном случае все внешние рециклы становятся внутренними рециклами одного аппарата. В связи с этим меньшее количество реагентов проходит дополнительную переработку или дополнительная их переработка исключается полностью. Следовательно, сокращаются потери реагентов, и повышается степень их использования.
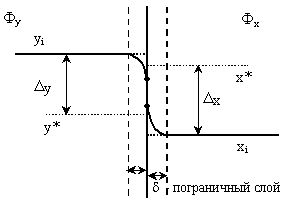
4.4 Совмещенный процесс абсорбции с химической реакцией (хемосорбция) Движущей силой массообменного процесса является отклонение от состояния равновесия. Состояние равновесия определяется равенством химического потенциала компонента в одной и другой фазе. Химический потенциал – энергия взаимодействия одной молекулы со всеми окружающими молекулами, при этом концентрации в фазах отличны друг от друга. Движущей силой процесса массообмена является разность между рабочей концентрацией компонента в аппарате и равновесной концентрацией этого компонента в этой же фазе по отношению к другой фазе.
Рис. 6 Профиль распределения концентрации абсорбтива в фазах при процессе хемосорбции.
Фx
– жидкая фаза (A
+ B),
Фy
– газовая фаза. хi,
yi
– рабочая концентрация компонента i
в жидкой и газовой фазе, х*,
y*
– равновесная концентрация компонента
i в жидкой и газовой фазе. Существует
предположение, что на границе раздела
фаз мгновенно устанавливается
равновесие. Уравнение равновесия:
y*=f(xi),
Хемосорбция – процесс, когда компонент i переходит в жидкую фазу и вступает в химическую реакцию. При этом скорость химической реакции ускоряет процесс разделения в I раз
где
I
– коэффициент ускорения хемосорбции;
За счет химической реакции, проходящей в жидкой фазе при хемосорбции, рабочая концентрация абсорбтива в жидкой фазе хi снижается, соответствующая ей равновесная концентрация в газовой фазе y* снижается и следовательно растет движущая сила процесса y (рис. 6).
4.4.1 Стадии процесса массопередачи с химической реакцией.
Механизм процесса массопередачи сложен и включает ряд стадий. Скорость процесса является сложной функцией параметров нескольких процессов: 1. Диффузия одного или нескольких реагентов из объема фазы Фy к границе раздела фаз. На границе раздела фаз можно предположить установление физического равновесия во всех случаях, когда концентрации реагентов вблизи границы в обеих фазах конечны. 2. Диффузия реагентов от поверхности раздела в объем фазы Фx. 3. Химическая реакция в фазе Фx. 4. Диффузия реагентов, первоначально присутствующих в фазе Фx, и (или) продуктов реакции в пределах собственно фазы Фx, обусловленная градиентом концентраций за счет протекания химической реакции. Все эти стадии протекают одновременно. Если 1-я стадия очень медленная, а реакция в Фx фазе достаточно быстрая, то абсолютное знание скорости химической реакции неважно. Т.е. 1-я фаза является лимитирующей, и ускорение достигается только за счет увеличения движущей силы. Это бывает редко. Обычно диффузия в газообразной фазе не является лимитирующей, так как высока величина свободного пробега молекул. В остальных случаях, когда лимитируют процессы в исходной фазе, возможны различные варианты моделирования течения процесса в зависимости от соотношения скоростей диффузии и химического превращения. Стадии 2 - 4 могут протекать одновременно и таким образом взаимно накладываться; суммарный результат этих стадий осуществляется после стадии 1. Если, например, стадия 1 определяет скорость, то общая скорость не зависит от химической реакции и процесс может рассматриваться как простое явление массопереноса, которое не зависит от скорости реакции. Сама химическая реакция может быть причиной высокой общей скорости массопереноса в пределах фазы 2 и поэтому стадия 1 будет лимитировать скорость. Интересен также анализ массопередачи с химической реакцией, когда скорость суммарного явления стадий 2 - 4 лимитирует процесс. 4.4.2 Общие математические основы процесса хемосорбции. В литературе представлен ряд гидродинамических моделей поверхности раздела системы жидкость - газ. Некоторые из них будут здесь обсуждены. Все гидродинамические модели основаны на предположении о нулевом градиенте скорости в жидкости. Однако необходимо напомнить, что условие нулевого градиента скорости у границы раздела системы газ - жидкость является не очень строгим применительно к теории химической абсорбции, хотя можно показать, что в большинстве случаев отношение скоростей массопереноса в жидкости при наличии или отсутствии химической реакции не зависит от частных гидродинамических условий в ней. Пленочная теория. Первой гидродинамической моделью, предложенной для исследования процессов переноса, была модель, основанная на пленочной теории. Она предполагает, что вблизи поверхности раздела любой текучей среды имеется неподвижная пленка толщиной , процессы переноса через которую происходят путем молекулярной диффузии. Условия в объеме рассматриваемой фазы должны быть постоянными с единственным исключением собственно пленки, так что общая движущая сила полностью используется явлением молекулярного переноса в пленке.
В
случае применения к процессу абсорбции,
лимитированному сопротивлением в
жидкой фазе, модели пленочной теории
скорость абсорбции через единицу
поверхности,
где с - концентрация абсорбированного компонента в жидкой фазе; х - расстояние от границы раздела фаз (за положительное принято направление от границы раздела фаз в жидкую фазу); D1 - коэффициент молекулярной диффузии абсорбируемого компонента в жидкости; ux - скорость переноса компонента по нормали к поверхности раздела. Если поверхность предполагается плоской, то
и градиент концентраций будет постоянным в пределах пленки, если не наложены какие-либо дополнительные условия (например, как при наличии химической реакции)
где с0 и c0 - значения с на поверхности раздела и в объеме жидкой фазы, соответственно. Коэффициент физической абсорбции k0L определяется уравнением
или
Уравнение (5) не дает какой-либо реальной новой информации о рассматриваемых процессах. В самом деле, толщина пленки , как и коэффициент абсорбции - неизвестны. Можно только полагать, что значение зависит лишь от гидродинамических условий в жидкой фазе. На основе уравнения (5) можно сделать вывод о том, что при одинаковых гидродинамических условиях коэффициент абсорбции должен быть пропорционален коэффициенту молекулярной диффузии. Эмпирическая корреляция коэффициентов абсорбции (при лимитировании процесса сопротивлением в жидкой фазе) в форме соотношений между критериями Стэнтона, Рейнольдса и Шмидта имеет вид:
Здесь uL - характеристическая скорость жидкости; L - характеристический линейный размер; L - кинематическая вязкость жидкости; а1, а2, а3 - численные постоянные. Лучшие результаты по уравнению (6) получены при а3 = 0.5; следовательно, по уравнению (6) при одинаковых гидродинамических условиях имеем
что по форме отличается от уравнения (5). В случае контакта жидкой фазы с твердой или намного более вязкой жидкой фазой k0L будет пропорционален коэффициенту диффузии в степени 2/3, что снова не соответствует уравнению (5). Следовательно, можно сделать вывод о том, что пленочная теория противоречит экспериментальным фактам. Тем не менее, при решении ряда теоретических проблем в области химической абсорбции встречаются такие математические затруднения, что само решение возможно только для наиболее простой модели, основанной на пленочной теории. Решение на основе пленочной теории можно считать в любом случае как приемлемое первое приближение. Особенно если рассматривается отношение коэффициента абсорбции в присутствии химической реакции kL к значению k0L. Если уравнение для этого отношения содержит только толщину пленки, то можно использовать уравнение (5) для выражения величины I как функции k0L:
Теория проникновения (модель Хигби) В 1935 г. Хигби предложил модель гидродинамических условий в жидкой фазе вблизи границы раздела жидкость - газ, которая основана на следующих гипотезах. Поверхность раздела газ - жидкость состоит из небольших элементов жидкости, которые непрерывно подводятся к поверхности из объема жидкости и наоборот уходят в объем за счет движения самой жидкой фазы. Каждый элемент жидкости, пока находится на поверхности, можно рассматривать как неподвижный, а концентрацию растворенного газа в элементе - всюду равной концентрации в объеме жидкости, когда элемент подводится к поверхности. В таких условиях абсорбция осуществляется при нестационарной молекулярной диффузии в различных элементах поверхности жидкости. При рассмотрении массопереноса из цилиндрического газового пузыря Хигби принял допущение, что все поверхностные элементы находятся на поверхности в течение одинакового количества времени, а именно
где d - вертикальная длина пузыря; ub —скорость. Нестационарный процесс молекулярной диффузии в пределах каждого элемента жидкости описывается обычным дифференциальным уравнением
где t - время, прошедшее от момента доставки рассматриваемого элемента поверхности к границе раздела фаз. Краевые условия к уравнению (10) запишутся в виде:
Здесь уравнение (11) вытекает из предположения о первоначальной концентрации; уравнение (12) дает определение концентрации на границе раздела фаз c0 и (13) может использоваться как второе граничное условие, если даже к концу времени существования элемента t* концентрация в его пределах заметно отличается от первоначальной величины c0 в поверхностных слоях элемента. Последнее предположение может также рассматриваться как условие, что «глубина проникновения» (т.е. расстояние от поверхности раздела, на котором с заметно отличается от c0) будет по истечении времени t* намного меньше, чем глубина самого элемента поверхности. Следует отметить, что в некоторых случаях, например в пленочных колоннах, условие (13) должно быть заменено условием нулевого градиента концентраций на некотором конечном расстоянии от поверхности. Интегрирование уравнения (10) легко выполнить, применив преобразование Лапласа:
Тогда уравнение (10) примет вид
где граничное условие (11) уже удовлетворено. Интеграл уравнения (15) будет иметь вид:
где функция erfc(z) определяется следующим образом:
Производная
а мгновенная скорость абсорбции в элементе определяется уравнением:
Уравнение (19) определяет скорость абсорбции в элементе, возраст которого, т.е. время его пребывания на поверхности, равен t. Средняя скорость абсорбции в течение всего времени существования элемента t* будет:
Из определения коэффициента абсорбции по уравнению (4) следует:
Из уравнения (21) видно, что k0L пропорционально коэффициенту диффузии в степени 1/2, что подтверждается экспериментально. Конечно, уравнение (21) можно непосредственно использовать для вычисления k0L только в тех случаях, когда известно t*, как, например, в случае движения пузырьков газа. При подстановке уравнения (9) в (21) получим для данного случая:
Здесь
Уравнение (22) удовлетворительно подтверждается экспериментальными данными в случае пузырьков средних размеров. Оно также приемлемо для случая жидких капель при достаточно низкой вязкости дисперсной фазы. Во всех случаях, когда t* неизвестно, по уравнению (21) можно определить эквивалентное время существования элементов поверхности. Теория проникновения (модель Данквертса) Если отказаться от допущения о равном времени существования элементов поверхности, то среднюю скорость абсорбции можно определить как
где (t)dt - доля общей поверхности, занимаемая элементами с возрастом от t до (t + dt). Функция (t) называется функцией распределения возраста элементов и удовлетворяет очевидному условию:
Уравнение (23) не может быть проинтегрировано без предположения о специфической форме функции распределения возраста. Тем не менее, можно заметить, что какой бы ни была форма функции распределения, уравнение (23) всегда обеспечивает требуемую пропорциональность k0L и (D)1/2. Данквертс выбрал аналитическую форму для (t), которая основывается на следующем предположении. Допустим, что вероятность обновления данного элемента жидкости в определенном промежутке времени не зависит от его возраста. В этом случае скорость обновления поверхностных элементов с любым данным возрастом будет пропорциональна числу имеющихся элементов этого возраста, отсюда
где s - коэффициент пропорциональности. В результате интегрирования уравнения (25) получаем:
Подстановка уравнения (26) в (24) показывает, что требуемая константа s; отсюда:
Подставляя уравнение (27) в (23), имеем:
Величина s имеет физический смысл скорости обновления поверхности и 1/s может рассматриваться как средний возраст поверхностных элементов. Сравнение уравнений (21) и (28) показывает, что в любом случае коэффициент абсорбции пропорционален квадратному корню из отношения коэффициента диффузии к возрасту элементов поверхности, причем коэффициент пропорциональности близок к 1. Кроме тех случаев, для которых при использовании модели Хигби величину t* можно рассчитать независимым путем, для определения t* и s применяют уравнения (21) и (28). Здесь и далее предполагается опустить различие между моделями Хигби и Данквертса и определять «эквивалентное время диффузии» tD с помощью уравнения:
4.4.3 Диффузия, реакция и время пребывания. Выше было показано, что пенетрационная теория приводит к приемлемым выражениям для коэффициента абсорбции, таким как уравнения (21) и (28). Оба уравнения могут быть приведены к форме (29), которая определяет время диффузии tD. По физическому смыслу последнее является средним возрастом элементов поверхности жидкости, т.е. промежутком времени, достаточным для полного перемешивания. Величины tD в промышленных абсорберах можно оценить либо непосредственно при исследовании гидродинамики жидкости, либо по уравнению (29) в сочетании с корреляциями для коэффициентов абсорбции. Проанализируем порядок величин для двух важнейших типов абсорберов. Если газ барботирует через слой жидкости, величину tD можно определить по уравнению (9). Обычные диаметры пузырьков составляют 0.2 – 0.6 см; скорости движения пузырьков 15 - 35 см/сек. При этих значениях интервал величин tD будет
и по уравнению (29), принимая D1 равным 10-5 см2/сек (для растворенного газа в не слишком вязкой жидкости), получим:
Интервал, указанный в уравнении (31), подтверждается экспериментально. Для насадочной колонны обычные значения высоты единицы переноса при лимитировании массопередачи сопротивлением в жидкой фазе составляют от 20 до 80 см:
Здесь VL — объемная скорость жидкости на единицу поперечного сечения (фиктивная скорость жидкости); а - эффективная площадь поверхности раздела фаз на единицу объема. Значение VL составляет ~ 0.15 см/сек; значение а очень неопределенно, но может считаться приемлемой величина 0.1 см-1. Отсюда, k0L ~ 0,03 см/сек, и интервалы, указанные в уравнениях (30) и (31), можно рассматривать как применимые и к насадочным колоннам. В анализе химических реакций очень полезным является понятие «время реакции». Его можно определить как
r - скорость реакции; c - действительная концентрация рассматриваемого реагента; с - равновесная концентрация реагента. Для простой реакции первого порядка с константой скорости k
Физический смысл времени реакции - время, необходимое для протекания реакции. За исключением только реакции первого порядка, время реакции в общем случае зависит от рассматриваемой концентрации; это обусловлено нелинейной зависимостью химических процессов от величины их движущей силы. Напомним, что время диффузии зависит от гидродинамических условий, так как оно является временем процесса нестационарной диффузии в пределах элементов поверхности жидкости; время же реакции зависит только от кинетики рассматриваемой реакции и не является фактически достижимым временем реакции, а только временем, необходимым для нее. Как было показано выше, время диффузии tD практически изменяется в узком интервале. В отличие от этого времена реакции, рассчитанные для практических систем, могут различаться существенно. Наконец, следует рассмотреть третье характеристическое время - время, действительно доступное для реакции. Последнее является, по-видимому, общим временем пребывания жидкой фазы tпр в рассматриваемом абсорбере, так как химическая реакция происходит в жидкой фазе. По-видимому, если рассматривать процесс химической абсорбции в целом, то величина tпр должна иметь, по крайней мере, тот же порядок, что и tр. Действительно, если tр будет намного больше, чем tпр, тогда никакой реакции в жидкой фазе вообще не будет и рассматриваемый процесс фактически будет процессом физической абсорбции. 4.4.4 Реакционно-диффузионные дифференциальные уравнения Дифференциальные уравнения, отражающие протекание одновременных процессов диффузии и химической реакции в жидкой фазе, могут быть записаны для каждого реагирующего компонента в форме
где
Аналогичная векторная запись использовалась Бердом, Стюартом и Лайтфутом [I].
Для
гидродинамических условий, предполагаемых
в моделях пленочной и пенетрационной
теорий, уравнение (34) значительно
упрощается. Действительно, для обеих
моделей и
= 0, а в
случае пленочной теории также и
Важно выяснить физический смысл и и t. Уравнение (34) записано в системе координат, которая движется вместе с рассматриваемым поверхностным элементом. Отсюда равенство и = 0 означает, что поверхностный элемент жидкости за время своего существования ведет себя как абсолютно твердое тело, но это не значит, что его положение в пространстве неизменно. С этой точки зрения, величина t - возраст элемента жидкости или, иными словами, время, отсчитываемое от момента доставки элемента жидкости к поверхности. В связи с этим уравнение (34), описывающее нестационарное состояние, может быть с успехом применено к стационарным в макроскопическом масштабе процессам. Уравнение (23) показывает, как явление, описанное уравнениями (10) - (13), которое является чисто нестационарным, пока рассматривается каждый поверхностный элемент, результируется в макроскопически стационарный процесс, при условии, что функция распределения возраста элементов неизменна во времени. Модель пленочной теории предполагает, что рассматриваемое явление даже в микроскопическом масштабе настолько отвечает условиям стационарности, что член из уравнения (34) выпадает. Здесь возможны дальнейшие упрощения, если предположить, что поверхность раздела газ - жидкость плоская, или, более точно - если кривизной поверхности жидкости можно пренебречь. В случае пленочной теории это допущение означает, что минимальный радиус кривизны поверхности Rкр намного больше толщины пленки
и в случае пенетрационной теории
где
Действительная глубина проникновения почти равна . В самом деле, химическая реакция всегда вызывает более крутое увеличение градиента концентраций на единице расстояния вблизи поверхности раздела фаз. Уравнения (35) и (36), как будет показано ниже, должны всегда выполняться, когда
Хотя в литературе рассмотрены [2, 3] также и специфические задачи, для которых должна учитываться кривизна поверхности раздела газ - жидкость, условие (36) может рассматриваться как выполнимое в любом практическом случае. Следовательно, уравнение (34) может быть упрощено: для пенетрационной модели
для пленочной модели
Следует отметить, что уравнение (37) переходит в уравнение (10) при r = 0. Даже в упрощенной форме уравнение (37) далеко не всегда может быть решено. В общем случае r является функцией концентраций более чем одного реагента и, следовательно, математическая проблема состоит в интегрировании системы дифференциальных уравнений вида (37). Эта общая проблема не может быть решена. Даже система дифференциальных уравнений вида (38) требует для своего решения ряда аппроксимаций. Тем не менее, если рассматривать очень простые выражения для r, то может быть предложен ряд асимптотических решений. Граничные условия. Ограничимся рассмотрением системы только с двумя реагентами, а именно абсорбируемый компонент и нелетучий жидкий реагент. Пусть b - концентрация последнего и с – концентрация первого на расстоянии х от поверхности раздела газ - жидкость. Пусть D2 будет коэффициентом диффузии нелетучего реагента. У поверхности раздела газ - жидкость концентрация абсорбируемого компонента равна его растворимости при определенном парциальном давлении на границе раздела фаз , (39) в то время как нелетучесть жидкого реагента накладывает условие отсутствия его массопереноса к границе раздела фаз:
Шервуд и Вей [4] установили, что для ионных компонентов движущая сила массопередачи не адекватна просто градиенту концентраций. В этом случае условия отсутствия массопереноса могут создаться при конечном градиенте концентраций на поверхности раздела. Согласно пенетрационной модели, распределение концентраций в нулевой момент времени может быть записано как
где b0 и c0 - концентрации двух реагентов в объеме жидкости. Условием, определяющим решение задачи, является второе условие по пространственной координате. В случае пленочной модели это условие имеет вид:
В
случае пенетрационной модели то же
самое условие будет выполняться при
,
(44) При более тщательном подходе всякий раз, когда концентрация в объеме c0 равна равновесной концентрации с', или, когда r = 0 в объеме жидкости, следует руководствоваться граничными условиями (43) или (44). Это может быть показано интегрированием уравнения (38) от границы раздела фаз до расстояния , где с = с':
Из уравнения (45)
Члены
правой части уравнения (46) выражают
мгновенную скорость абсорбции, общую
скорость накопления абсорбирующегося
компонента и общую скорость реакции.
Их алгебраическая сумма равна нулю
только при условии, если величина
условие
где значение определяется дифференциальным уравнением:
В таких случаях интегрирование уравнения (38) переходит в проблему «движущейся границы» [5 -8].
4.5 Методы исследования реакционно-массообменных процессов. Рассмотрим основные этапы исследования неоднородных совмещенных реакционно-массообменных процессов на примере непрерывных реакционно-ректификационных процессов. Первый этап - анализ статики процессов. В процессе анализа статики непрерывных совмещенных реакционно-ректификационных процессов решаются следующие задачи: 1) определение составов и числа фракций, на которые может быть разделена реакционная смесь методом ректификации; 2) определение параметров химического равновесия; 3) определение возможных значений степени превращения реагентов и выхода продуктов; 4) выбор заданного разделения в реакционно-ректификационной колонне, содержащей реакционную зону; 5) синтез отдельных комплексов аппаратов функционального действия и всех вариантов принципиальной технологической схемы; 6) выбор оптимального варианта технологической схемы. На втором этапе решаются задачи математического моделирования реакционно-ректификационного процесса в такой последовательности: 1) создание или выбор из имеющихся математической модели совмещенного процесса; 2) выполнение машинного эксперимента с целью поиска возможных стационарных состояний, исследовании влияния различных параметров на результаты совмещенного процесса; 3) выбор оптимальных параметров; 4) расчет аппаратов, в которых проводится совмещенный процесс. Решение данных задач предусматривает создание методов расчета реакционно-массообменных процессов, обладающих устойчивой сходимостью. На третьем этапе проводят моделирование технологической схемы, включающей как составную часть непрерывный совмещенный реакционно-массообменный процесс. На четвертом этапе предусматривается проверка работоспособности реакционно-ректификационного аппарата и схемы в целом методом натурного эксперимента. Здесь же проверяется адекватность используемых моделей, подбирается необходимый катализатор и анализируется качество получаемых продуктов. Математические модели для расчета реакционно-массообменных процессов можно подразделить на две группы. К первой группе относятся модели, разработанные на уровне условий фазового равновесия, в которых используется понятие теоретических ступеней разделения. В моделях такого типа не рассчитывается кинетика массопереноса. Ко второй группе относятся модели, которые учитывают влияние химической реакции на коэффициенты и движущие силы процесса массопереноса.
4.6 Математическое моделирование и расчет реакционно-массообменных процессов. Первой была создана и наиболее широко распространена в настоящее время модель совмещенного процесса, основанная на концепции теоретической тарелки, на которой происходит химическое взаимодействие. Эта модель относительно проста, но при сопоставлении результатов, полученных на ее основе для ряда систем синтеза сложных эфиров, с экспериментальными данными была установлена удовлетворительная согласованность. К моделям этого же класса можно отнести модели, описывающие процессы, в которых реакция протекает достаточно быстро, предполагающие, что на тарелке (контактном устройстве) устанавливается химическое равновесие. Отдельный класс представляют математические модели, учитывающие кинетику межфазного массопереноса. Модели этого класса используются преимущественно для описания совмещенных процессов в аппаратах с непрерывным изменением состава фаз. Оценка параметров подобных моделей представляет сложную кинетическую задачу, к тому же в данном случае критериальная теория подобия является в принципе неприемлемой. Отметим, что в настоящее время отсутствуют систематические исследования, позволяющие сделать однозначный вывод относительно преимущества данного класса моделей в отношении их адекватности объекту по сравнению с классом, представленным выше. Наконец, известны модели РМП, построенные на основе информационного подхода. Широкого распространения данные модели пока не получили. Замечания, которые были сделаны относительно моделей, учитывающих реальный массоперенос, справедливы и для них. Таким образом, модель, основанная на понятии теоретической тарелки, является, с одной стороны, простой, а с другой - достаточно надежной и универсальной, ею мы и будем пользоваться в дальнейшем. Среди задач расчета реакционно-массообменного аппарата, так же как и в случае ректификации, можно выделить проектные и поверочные. Поверочная задача решается, когда тип аппарата, а также режимные параметры его работы (эффективность, флегмовое число, задержка жидкой фазы в реакционной зоне, уровень подачи и состав питания, отношение количеств отбираемого дистиллята к кубовому продукту и др. определены, требуется определить распределение компонентов по высоте колонны и составы кубового продукта и дистиллята. При проектной постановке задачи задают требования, определяющие кондицию продуктовых потоков (они, в свою очередь, могут определять степень превращения реагентов и селективность химического превращения), требуется определить технологические параметры совмещенного процесса, обеспечивающие получение продуктовых потоков необходимого состава. Поверочной постановке задачи расчета соответствует своего рода эксперимент, проводимый с использованием математической модели. Поэтому поверочный расчет иногда называют вычислительным экспериментом. Очевидно, задача в проектной постановке может быть решена посредством серии поверочных расчетов, в каждом из которых технологические параметры процесса меняют по сравнению с предыдущим значением таким образом, чтобы обеспечить выполнение предъявляемых к составу продуктовых потоков требований.
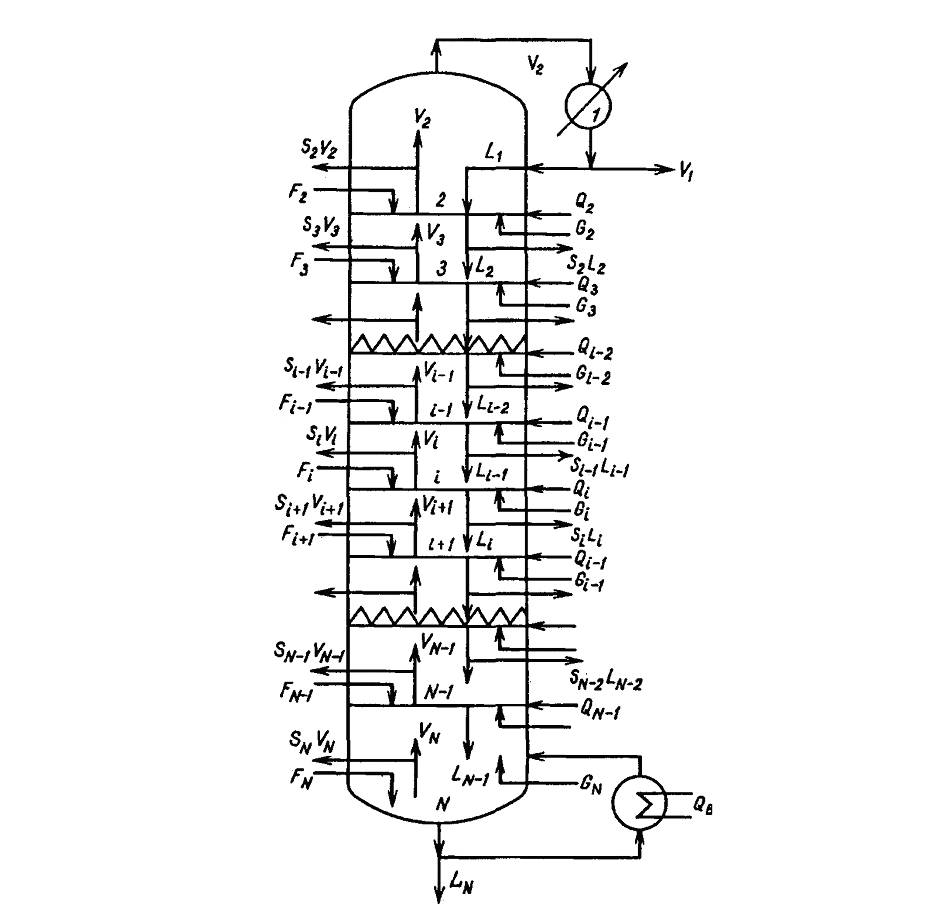
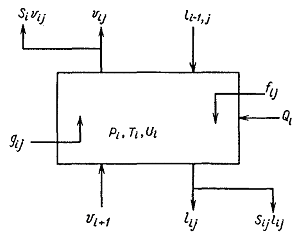
Рис. 7 Схема материальных потоков в реакционно-ректификационном аппарате. 4.7 Построение математической модели Рассмотрим N-ступенчатую колонну, в которой осуществляется реакционно-ректификационный процесс. Реакционная смесь включает с компонентов. Схема аппарата приведена на рис. 7. Ступень с номером 1 является полным конденсатором, ступень с номером N - парциальным кипятильником. Примем, что химические реакции протекают в жидкой фазе на каждой тарелке. Считаем, что: 1) процесс достигает стационарного состояния; 2) каждая ступень (тарелка) соответствует реактору идеального смешения (таким образом, состав жидкости на каждой тарелке является гомогенным и совпадает с составом жидкости, покидающей ступень); 3) пар и жидкость, покидающие тарелку, находятся в равновесии. Степень протекания жидкофазной реакции на каждой ступени определяется с помощью кинетического уравнения для односторонней или двухсторонней химической реакции. На рис. 8 приведена схема материальных потоков на реакционно-дистилляционной ступени (тарелке аппарата). Выделим три типа функций, описывающих физические и химические процессы на ступени i: Покомпонентный материальный баланс:
где
Si
и si
- боковые отборы пара и жидкости с i-ой
ступени;
Последнее слагаемое в уравнении 1 соответствует количеству j-го вещества, полученному за счет химического превращения. Энергетический баланс:
где H и h - мольные энтальпии паровых и жидких потоков. Данные уравнения взаимосвязаны с уравнениями покомпонентного материального баланса. Равновесие соотношения:
В уравнении (51) Qij выведено из определения Кij:
х и у - мольные доли компонентов в жидкости и паре. Набор рабочих параметров, т.е. совокупность параметров, определяющих режим реакционно-массообменного процесса, установившийся в аппарате, включает: 1) общее число ступеней; 2) номера тарелок, на которые подается питание, отбираются материальные потоки (боковые отборы) по высоте колонны, 3) режим теплообмена на контактных устройствах; 4) давление на каждой из ступеней, а также задержку на них жидкой фазы; 5) составы потоков, подаваемых на ступени.
Рис. 8 Схема материальных потоков на тарелке аппарата При этом остается возможность задать N переменных перед тем, как мы приступим к решению N(2c+1) уравнений для соответствующих N(2c+1) итерируемых переменных. Если в качестве задаваемых N переменных выступают скорости передачи энергии в виде тепла на каждую из ступеней, то уравнения решают для 2cN мольных потоков компонентов и N температур на каждой из тарелок. Однако режимы работы конденсатора и кипятильника зависят друг от друга и в общем случае могут быть заданы независимо только в узком, заранее неустановленном интервале значений, поэтому желательно в качестве задаваемых выбирать другие переменные.
Уравнение
материального баланса для полного
холодильника (конденсатора) будет
иметь отличную от уравнения (51) форму.
Обозначим покомпонентные мольные
потоки жидкого дистиллята:
где R -флегмовое число. Отметим, что состав дистиллята тот же, что и жидкости, стекающей из конденсатора, и поэтому равновесные соотношения не являются независимыми. Равновесное соотношение для компонента 1 заменяется уравнением точки кипения (компонент 1 должен присутствовать в дистилляте).
Так же как и уравнение энергетического баланса, остальные равновесные соотношения Q12 - Q1c замещаются уравнениями для покомпонентных флегмовых потоков, а именно:
В дальнейшем при составлении общей системы уравнений принят следующий поступенчатый порядок их группировки (Mi1, …, Mic, Ei, Qi1, …, Qic) с последующим дифференцированием по переменным
Такая последовательность при составлении уравнений и проведении их дифференцирования ведет к блочно-тридиагональной структуре матрицы Якоби с минимальной длиной блоков. Для достижения гибкости в выборе закрепленных при расчете переменных уравнения, определяющие их значение или соотношение между ними, включают в качестве дополнительных строк в нижней части стандартной системы, а дополнительные переменные - в качестве столбцов в правой части матрицы Якоби. Скорости химических превращений rin в жидкой фазе могут быть представлены уравнениями, в которых они выражены как функции от состава жидкой фазы и температуры. Задержкой паровой фазы и протеканием в ней химической реакции, как правило, пренебрегают. Напомним, что vj - стехиометрический коэффициент компонента j в -ой химической реакции является положительной величиной, если j-ый компонент образуется за счет -ой реакции. Одна из возможных форм записи уравнения для расчета скоростей химической реакции, соответствующая закону действующих масс, имеет следующий вид:
где
ciq
= liq/(LiLi)
-
концентрация компонента q;
Li
- мольный
объем жидкой фазы на тарелке с номером
i;
nq
- показатель степени; Ap
- предэкспоненциальный множитель
уравнения Аррениуса; Ep
- энергия активации; R
- универсальная
газовая постоянная; Ti
- температура на ступени i,
например,
для двухсторонней реакции
где p = 1 соответствует прямой реакции, р = 2 - обратной; k1 - положительная величина, k2 - отрицательная.
Используемые формулы
Пусть
Тогда
Используя
набла-оператор
Оператор
Лапласа
для скалярной функции
для
векторной функции
|

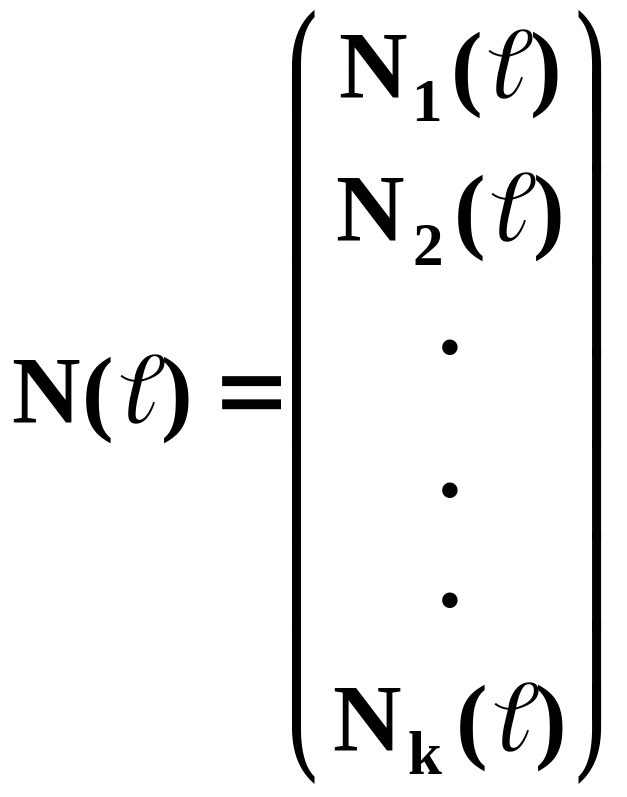 .
.
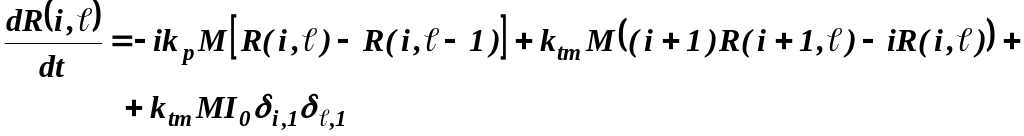 .(9)
.(9)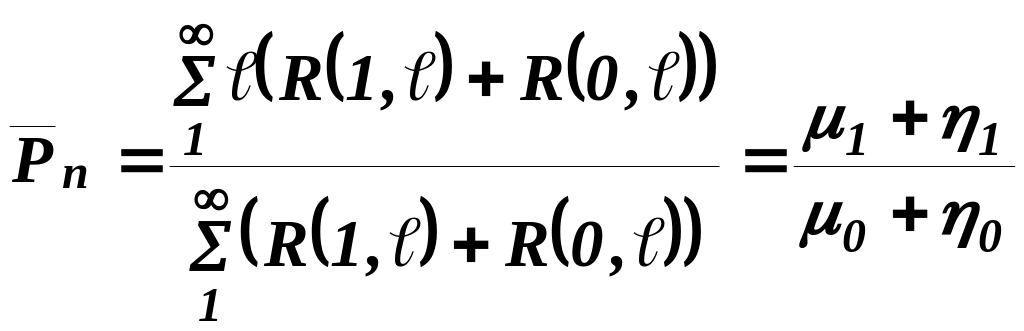 , (16)
, (16)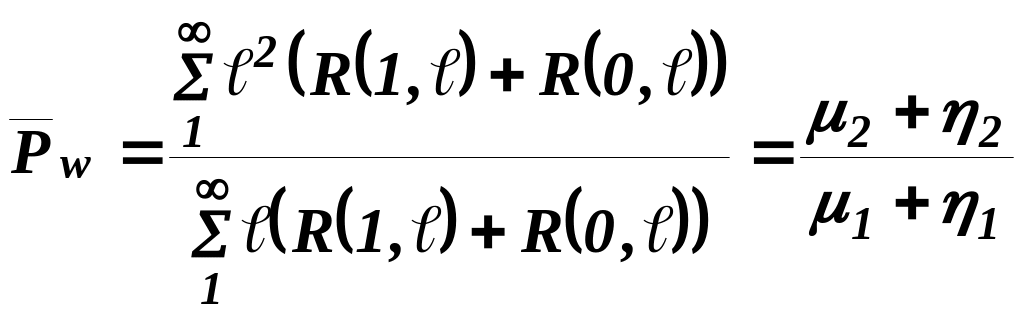 . (17)
. (17)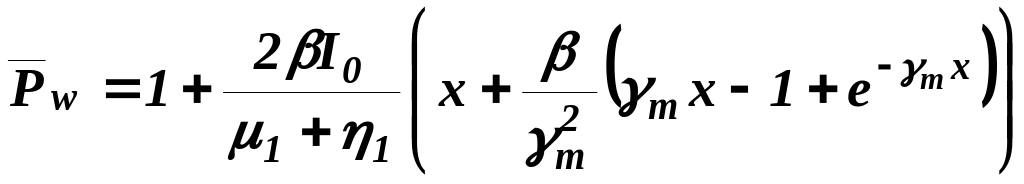 .
.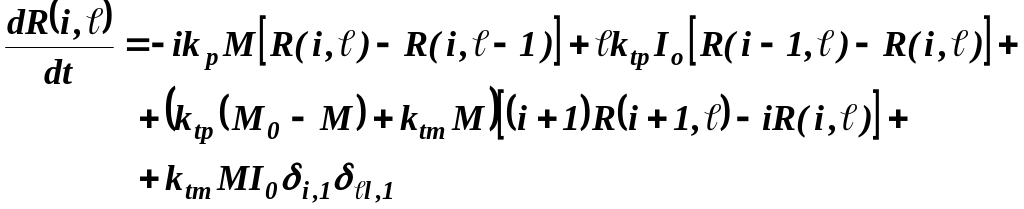 ,
(23)
,
(23)
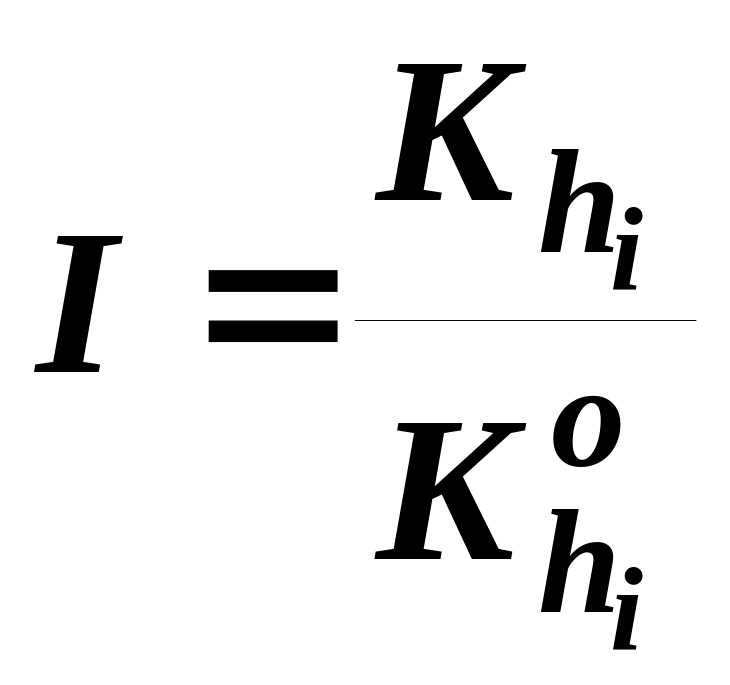 ,
,
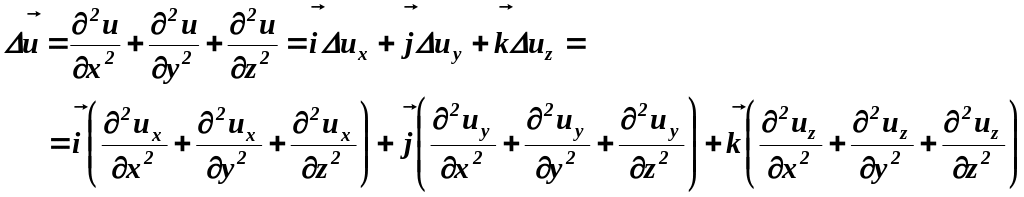 - это векторная функция.
- это векторная функция.