2.3.5 Уравнения переноса импульса

При выводе уравнений переноса импульса из общего уравнения переноса (27) в качестве потенциала переноса используется импульс единичного объема жидкости .

Скорость изменения импульса неизолированной системы равна сумме действующих на нее внешних сил.

На выделенный объем жидкости V, движущейся в поле силы тяжести, действуют поверхностные сжимающая сила давления и сила внутреннего трения. Если в рассматриваемую систему включить взаимодействующую с областью V жидкость, то силы внутреннего трения и давления можно рассматривать как внутренние для данной системы. Внешней силой остается сила тяжести, она характеризуется объемной плотностью притока импульса .

В этом случае в уравнении (27) -тензор плотности потока импульса:

.

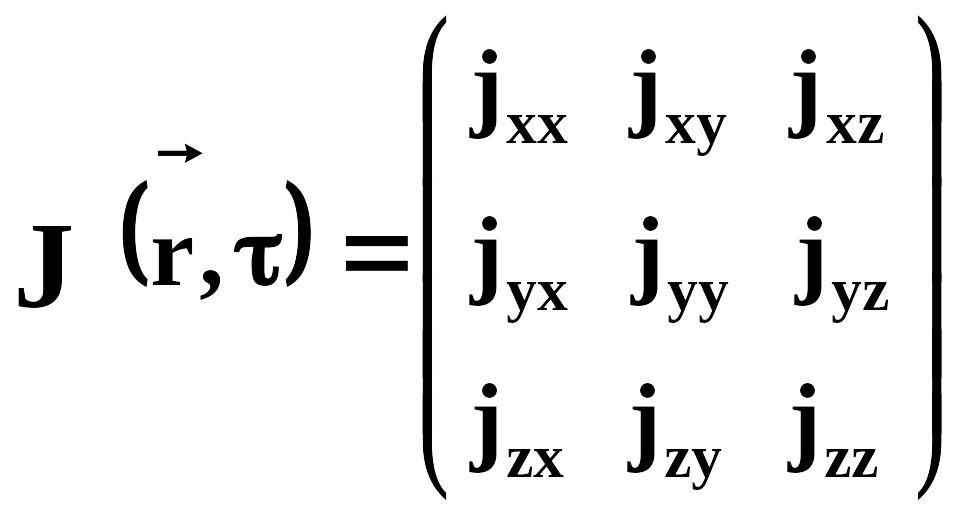Понятие тензора является обобщением понятия вектора (вектор-это тензор первого ранга).

Физический смысл компонент тензора таков: величина - это x-я компонента импульса, переносимого за единицу времени через единичную площадку, перпендикулярную оси Oy.

Тензор представим в следующем виде

,

где , р - гидростатическое давление, - единичный тензор, - тензор вязких напряжений.

Таким образом, - плотность потока импульса за счет конвекции; - плотность потока импульса за счет гидростатического давления; - плотность потока импульса за счет внутреннего трения жидкости.

Уравнения переноса импульса при течении несжимаемой ньютоновской жидкости имеют вид

, (41)

(41) - уравнения Навье-Стокса, здесь ,

.

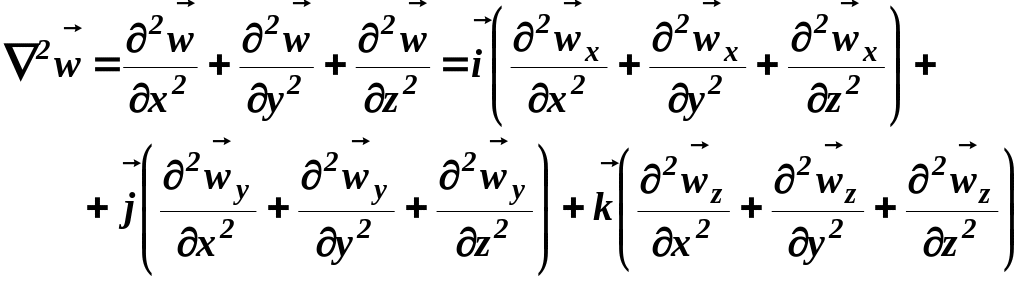Уравнения Навье-Стокса совместно с уравнением неразрывности потока (21), дополненные начальными и граничными условиями, описывают поля скоростей и давлений при течении несжимаемой вязкой жидкости. В случае идеальной жидкости (для которой можно пренебречь вязким трением) уравнения Навье-Стокса переходят в уравнения Эйлера

, (42)

Анализ движения вязкой жидкости с помощью уравнений Навье-Стокса проводят отдельно для ядра потока и для пограничного слоя.

2.3.6 Аналогия процессов переноса

Уже отмечалась идентичность уравнений, описывающих молекулярный перенос массы, теплоты и импульса (18), (19), (20), что объясняется сходством физических процессов переноса.

Описание конвективного переноса массы, теплоты и импульса единым уравнением (27) - основным уравнением переноса субстанций, также основано на сходстве физических процессов переноса.

В большей степени аналогичны процессы переноса массы и теплоты. Перенос импульса описывается более сложными уравнениями Навье-Стокса, так как, во-первых, импульс - это векторная величина, во-вторых, на перенос импульса в большей степени, чем на перенос массы и теплоты, влияют силы давления и тяжести.

2.3.7 Начальные и граничные условия к уравнениям переноса

Поскольку дифференциальные уравнения переноса имеют бесконечное множество решений, для выделения однозначного решения надо сформулировать краевые условия, которым удовлетворяют искомые функции.

Движущаяся среда может занимать либо неограниченную область, либо область, ограниченную поверхностью S, в которую входит и межфазная поверхность, если в среде имеются включения другой фазы (капли, пузыри, твердые частицы).

Решение нестационарных уравнений переноса находится для промежутка времени либо .

В качестве начальных условий используют задание потенциалов переноса во всей рассматриваемой области в начальный момент времени :

.

Более общей записью начальных условий является выражение

, (43)

где L – заданный оператор; - известная функция.

Граничным условием является выражение вида:

, (44)

где L – заданный оператор; - функция, заданная в точках граничной поверхности S.

граничные условия делятся на четыре типа:

1. граничное условие I рода получается из соотношения (44) при 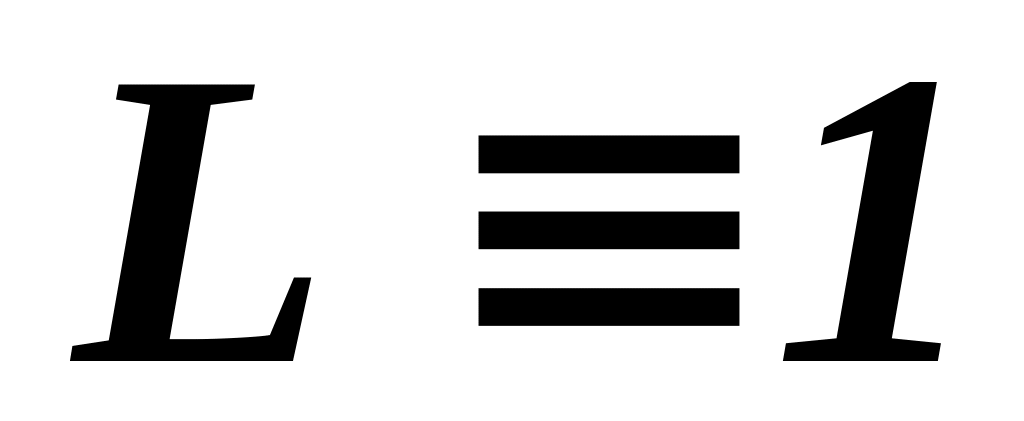, т.е. является заданием потенциала переноса на границе рассматриваемой области во все моменты времени.

2. граничное условие II рода получается из соотношения (44) при 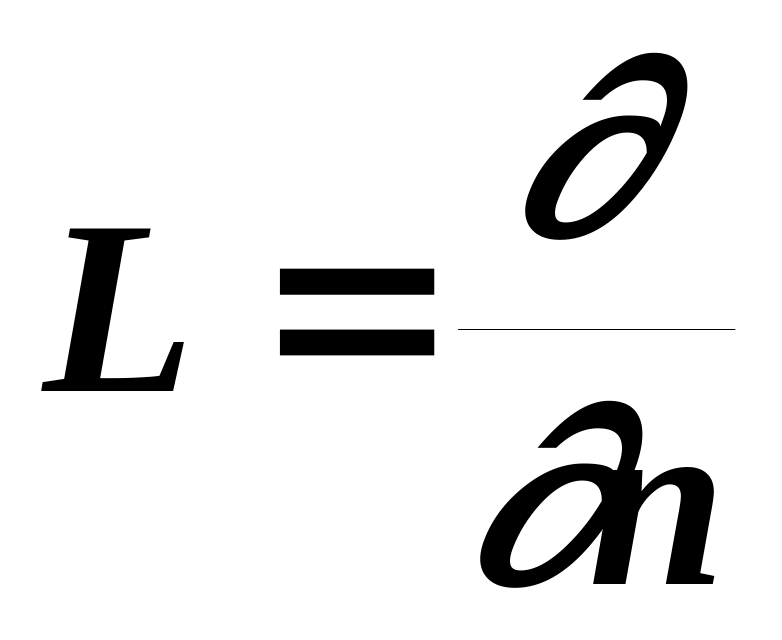, т.е. является заданием производной потенциала  по нормали к поверхности S в точках этой поверхности. Для уравнений переноса, в которых молекулярный поток переноса описан градиентным законом вида

,

граничное условие II рода является заданием величины плотности потока переноса на граничной поверхности

. (45)

3. граничное условие III рода состоит в задании некоторой комбинации значений потенциала переноса и его производной по нормали на границе рассматриваемой области. Обычно граничные условия III рода являются математической формулировкой условий конвективного тепло- и массообмена на границе:

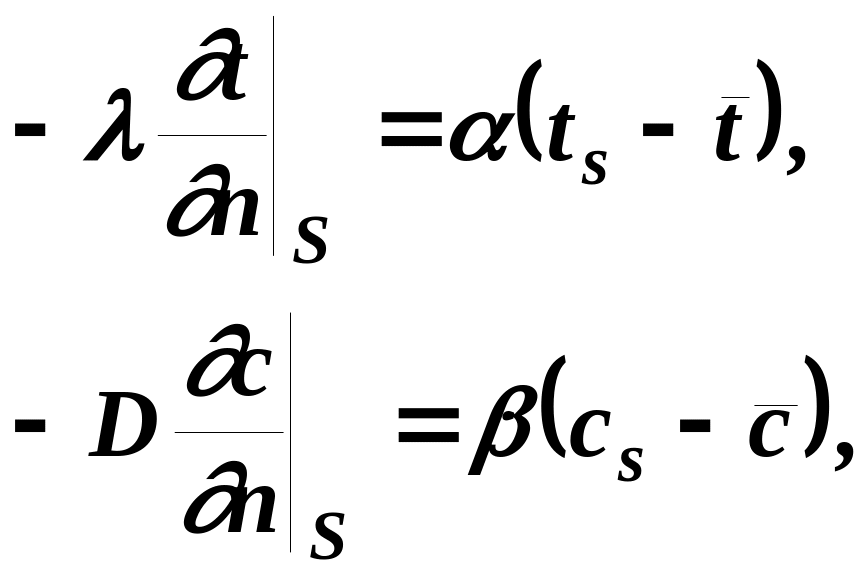(46)

здесь ,  - соответственно коэффициенты тепло- и массоотдачи, их введение эквивалентно введению эффективной толщины пограничного слоя, через который происходит перенос

где и - соответственно эффективная толщина теплового и диффузионного пограничных слоев на поверхности S, ограничивающей рассматриваемую область; , - соответственно средние температура и концентрация распределяемого вещества в ядре потока (т.е. на внутренней границе соответствующего пограничного слоя).

Для уравнений переноса импульса граничное условие I рода состоит в задании поля скоростей на границе движущегося потока. Например, экспериментально установлено, что при движении вязкой среды макроскопическая скорость на неподвижной поверхности обращается в ноль (условие прилипания).

граничное условие II рода состоит в задании тензора напряжений на ограничивающей поверхности, а граничное условие III рода является условием пропорциональности компонент тензора вязких напряжений и скоростей движения жидкости на границе области течения.

Граничные условия IV рода надо использовать при рассмотрении процессов переноса в двух смежных областях с различными свойствами и скоростями переноса. Например,

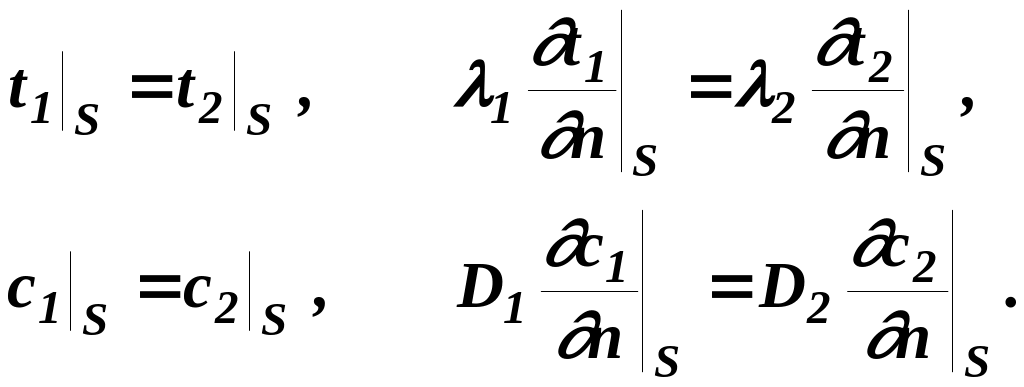(47)

граничные условия IV рода накладывают требование равенства потенциалов переноса и их молекулярных (диффузионных) потоков на поверхности раздела фаз.

Если среда занимает неограниченную область, то кроме условий (44)-(47) на границе раздела фаз, надо еще задать условия на бесконечности:

При решении уравнений переноса для симметричных пространственных областей с одинаковыми условиями на симметричных ограничивающих поверхностях используют условие сопряжения решений на оси или плоскости симметрии:

,

где - координатный вектор оси или плоскости симметрии.

Чтобы исключить решения, не имеющие физического смысла, используют условие конечности потенциалов переноса

.