6 Заключение

Интерференционная картина от двух точечных источников в вол­новой кювете характеризуется системой узловых линий, т. е. ли­ний, на которых вода остается невозмущенной. Когда источники находятся в одинаковых фазах, узловые линии располагаются сим­метрично относительно средней линии, т. е. перпендикуляра, вос­ставленного из середины прямой S₁S₂, соединяющей источники.

В непосредственном соседстве с источниками узловые линии искривлены, но уже довольно близко от источников они становятся почти прямыми. Продолжения этих прямых, проведенные в сторону источников, пересекаются в середине прямой, соединяющей источ­ники. Число узловых линий и угол, образуемый каждой из них с прямой S₁S₂, определяются отношением . Это означает, что, зная одну из величин, или , можно определить другую.

Даже при постоянной длине волны и постоянном расстоянии между источниками интерференционные картины различны в зави­симости от разности фаз р источников. При синфазных источниках образуется четное число узловых линий, расположенных симмет­рично относительно средней линии. Если же источник S₂ посылает гребни на время позже, чем S₁, то все гребни от S₂ имеют меньший радиус, чем соответствующие гребни от S₁. Соответственные ради­усы отличаются на отрезок l=рλ. Вследствие этого точки пересече­ния соответственных гребней от S₂ и впадин от S₁ расположены ближе к S₂. Это означает, что узловые линии загибаются от S₁ в сторону S₂ и картина становится несимметричной. Только при р=1/2 получается вновь симметричная картина, но в этом случае средняя линия совпадает с одной из узловых линий, а число узловых линий является нечетным.

Если расстояние между источниками и длины возбуждаемых волн постоянны, расположение интерферен­ционных линий зависит от разности фаз источников. Следовательно, для поддержания неизменной интерференционной картины разность фаз источников должна быть также постоянной. Для двух источ­ников, действующих с одинаковой частотой, разность фаз будет обя­зательно постоянной. Но если хотя бы один из источников будет нерегулярно включаться и выключаться, то разность фаз, а с нею и интерференционная картина будут изменяться. Интерференционные картины имеют огромное значение в интерференции любых волн.

ДОМАШНИЕ ЗАДАНИЯ

1 . Если бы вдоль спиральной пружины распространялась периодическая волна, каждый волновой импульс которой имел бы форму, изображенную на рис. 19, и если бы мы пожелали образовать узлы посредством посылки в обрат­ном направлении периодических волновых импульсов, то какую форму нужно было бы им придать? (раздел 1)

Рисунок 19. К задаче 1

2. На каком расстоянии от стенки (см. рис. 3) произойдет встреча волновых импульсов а и с с образованием следующего узла? (раздел 1)

3. При анализе рис. 1 – 3 было показано, что при падении периодических волновых импульсов на закрепленный конец спиральной пружины точка Р, находя­щаяся на расстоянии от закрепленного конца, все время остается в покое и по­тому является узлом. Продолжите те же рассуждения, чтобы доказать, что точка Р₂, находящаяся на расстоянии от того же конца, также является узлом.

4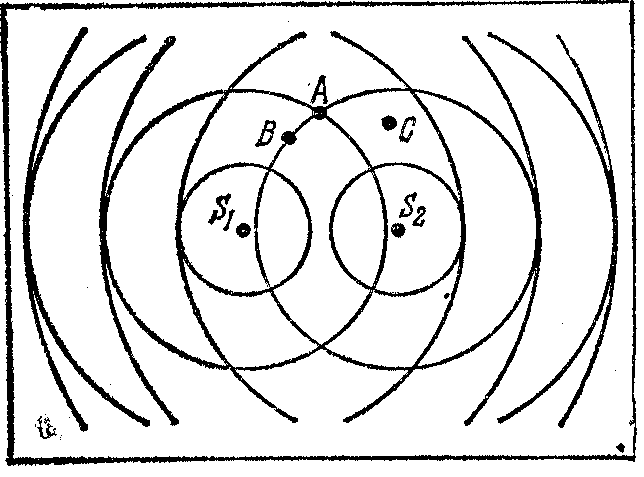 . На рис. 20 окружности изображают гребни волн, возбуждаемых источ­никами S₁ и S₂. В которых из точек А, В и С расположатся «удвоенный гребень», «удвоенная впадина» и узловая точка? (раздел 2)

Рисунок 20. К задаче 4

5. Постройте семейства концентрических гребней и узловых линий от двух ис­точников с расстоянием для моментов:

а) когда возбудители создают гребни;

б) когда возбудители создают впадины.

Как движутся усиленные гребни за время между этими двумя моментами?

6. Постройте интерференционную картину для случая , на листе бумаги достаточных размеров, чтобы можно было уместить прямолинейные участки уз­ловых линий. Проведите продолжения этих прямых обратно к области источников и удостоверьтесь в том, что эти продолжения пересекаются вблизи середины пря­мой, соединяющей источники.

7. Если на рис. 4 восставить перпендикуляр к прямой S₁S₂ в ее середине, то будет ли он узловой линией? (раздел 2)

8 . Сложите две полоски линованной бумаги шириной 2 см, как показано на рис. 21. Представьте себе, что линии на бумаге являются гребнями волн, а ваши пальцы изображают источники волн. Заметьте, где гребни от обоих источников на­кладываются друг на друга. Затем, вращая свободные концы полосок вокруг прижи­мающих пальцев, установите положения узловых линий и цепочек бегущих волн.

Рисунок 21. К задаче 8

9. Рассмотрите интерференционную картину от двух точечных источников. Затем выясните, что произойдет с узловыми линиями после помещения третьего источника, тождественного с остальными, посредине между ними?

10. Какая из узловых линий на рис. 10 образует геометрическое место точек Р, удовлетворяющих условию РS₁ ─ РS₂ = λ? (раздел 3)

11. Известно расстояние некоторой точки узловой линии от двух точечных источников в волновой кювете. Чего не хватает для вычисления длины волны? (Раздел 3.)

12. Используя метод, показанный на рис. 11, постройте узловые линии интерференционной картины от двух точечных источников для = 1/3. Отличает­ся ли этот метод от метода, описанного в задаче 6?

13. Что произошло бы с узловыми линиями, если бы один из двух источников стал постепенно ослабевать и наконец перестал бы работать?

14. В случае двух точечных источников, находящихся на расстоянии друг от друга, существует ли диапазон длин волн , создающих интерференционную картину без узловых линий? (раздел 4)

15. Два источника, расположенные на расстоянии 6 см друг от друга и ко­леблющиеся в одинаковой фазе, вызы­вают водяные волны с длиной волны 1,5 см. Постройте узловые линии вдали от источников, определяя их положение по точкам пересечения дуг окружностей с центрами в источниках. Измерьте угол между второй узловой линией и средней линией интерференционной картины. Сравните синус этого угла с величиной .

16. Придумайте интерференцион­ный опыт, способный доказать волно­вую природу звука и позволяющий измерять длины звуковых волн.

17. а) Используйте рис. 6 и рис. 9 для нахождения отношения с помощью формулы = .

б) На рис. 6 и рис. 9 интерференцион­ная картина уменьшена в 4 раза. Измерив на этих снимках, определите значение λ.

1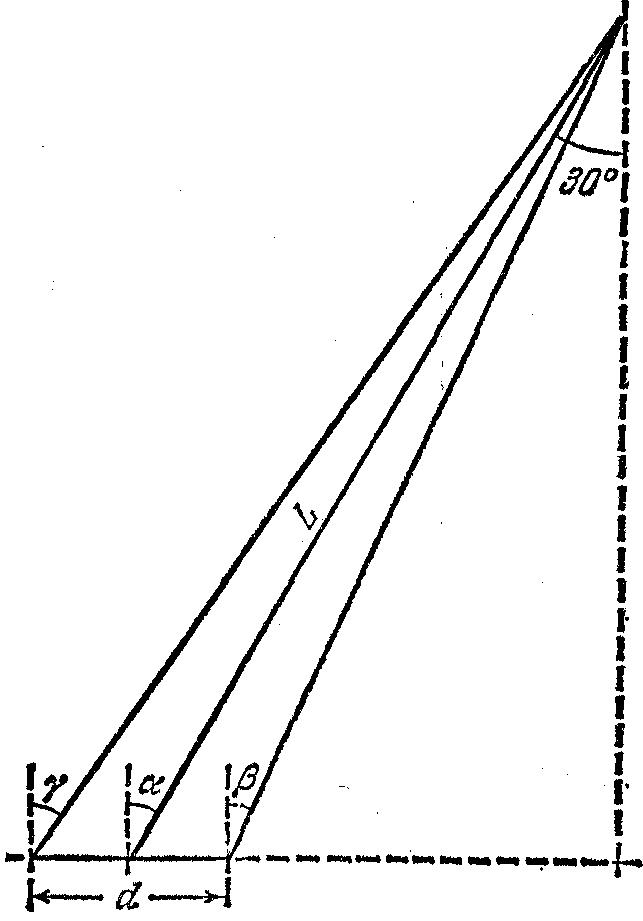 8. Вспомните или разыщите определение гиперболы и объясните, почему узловые линии расположены по гиперболами?

19. а) На рис. 22 L=50 см, =10 см, α = 30^о. Чему равны углы γ и β?

б) Найдите значение углов γ и β для L=500 см.

в) Убеждают ли вас полученные результаты в том, что можно с достаточно хорошим приближением полагать γ β α, когда L во много раз больше ?

Рисунок 22. К задаче 19

20. Красный и синий гоночные автомобили мчатся по круговому гоночному треку, имеющему 5 км в окружности. Их скорости одинаковы и постоянны. Каж­дый автомобиль затрачивает 2,5 мин на полный оборот. Синий автомобиль все время отстает на 0,5 мин от красного.

а) Каково отставание по фазе р синего автомобиля относительно красного?

б) Чему равна скорость автомобилей?

в) Если длину трека уменьшить до 4 км, то повлияет ли это на ответы по пунктам а) и б)?

21. На рис. 14 l = 0,25 см и λ=0,70 см. Каково отставание по фазе? (раздел 3)

22. Есть ли разница между отставаниями по фазе, равными нулю и единице (в долях периода)? (раздел 5)

23. Докажите, что для двух источников с разностью фаз р первая узловая линия может быть построена по точкам, для которых разность хода лучей от источ­ников равна .

24. Наблюдатель находится на большом расстоянии L от пары источников, создающих интерференционную картину. Перемещаясь по перпендикуляру к сред­ней линии, он должен пройти путь х, чтобы перейти со средней линии на первую узловую (см. рис.13).

а) Чему равна разность фаз источников, если х=0,008L, а λ=0,01 ?

б) Чему равна разность фаз источников, если λ=0,016 ?

25. Два точечных источника, образующих волны одинаковой длины λ, рас­полагаются в волновой кювете на расстоянии =5λ друг от друга.

а) Найти угол между прямолинейной частью первой узловой линии и сред­ней линией интерференционной картины при одинаковых фазах источников.

б) Найти для разности фаз источников р= .

в) Сколько получится узловых линий?

26. В радиоастрономии один из методов «просматривания» космического пространства можно сравнить с обратным использованием двухточечного генера­тора поверхностных волн в кювете, снаб­женного фазорегулятором (см. рис. 23). Наибольшая интенсивность сигнала дости­гается, когда сигналы, поступающие в С и D, находятся в одинаковой фазе.

Ф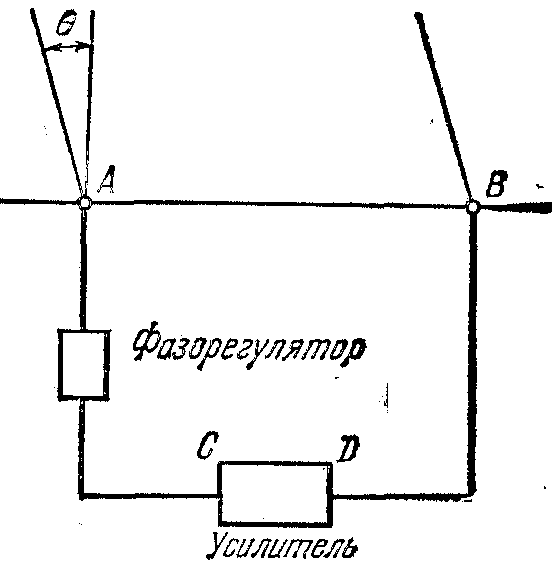 азорегулятор изменяет разность фаз путем изменения длины провода между А и С. Если длины проводов АС и ВD равны, то сигналы, принятые из точки, расположенной прямо «над головой», находятся в фазе. Чтобы «смотреть» по направлению, определяемому углом , провод АС должен быть удлинен. Если расстояние АВ составляет 100 м, частота, на которую настроен приемник, равна 2·10⁷ с^–1, какая разность фаз должна быть введена, чтобы «смотреть» под углом 5^о к вертикали?

Рисунок 23. К задаче 26

27. Обычные широковещательные радиостанции работают на длинах волн от 200 до 600 м. Антенны обычного типа представляют собой вертикальные мачты, которые в плоскости земной поверхности ведут себя как точечные источники волн.

а) Как надо расположить две антенны подобного типа в городе, растянувшемся узкой полосой вдоль берега моря, чтобы потери мощности на излучение в направ­лении как моря, так и ненаселенной местности были минимальными?

б) Если город растет по направлению в глубь материка, что нужно сделать, чтобы посылать наиболее интенсивные сигналы на новостройки?

28. Два источника волн колеблются в кювете с частотами 15 и 16 колебаний в секунду. Опишите получающуюся систему узловых линий.

29. Что будет происходить с интерференционной картиной от двух точечных источников волн, если разность фаз внезапно меняется?

18