3 Форма узловых линий

Изучив интерференционные картины на рис. 6 и 9, можно увидеть, что, хотя вблизи источника узловые линии слегка искрив­лены, с удалением от источников они вскоре совершенно выпрям­ляются.

Другой бросающийся в глаза факт заключается в том, что число узловых линий уменьшается с увеличением длины волны. Для облегчения дальнейшего обсуждения интерференционных картин пронумеруем узловые линии таким образом, чтобы затем было удобно на них ссылаться. Для этого вернемся еще раз к рис. 8 и удосто­веримся, что картина симметрична, т. е. выглядит совершенно одинаково справа и слева от центральной прерывистой линии. По­этому достаточно пронумеровать половину узловых линий, напри­мер те, которые расположены в правой половине картинки.

В соот­ветствии с этим первую узловую линию справа от центральной (прерывистой) назовем первой узловой линией. Следующую назовем второй узловой линией и т. д. Когда же мы хотим говорить об одной из узловых линий, но нас не интересует ее порядковый номер, будем называть ее n-й узловой линией, где п есть целое число (1, 2, 3 и т. д.).

О бозначим буквой Р произвольно выбранную точку на первой узловой линии и соединим ее прямыми РS₁ и РS₂ с источниками (рис. 10). Каждая из этих прямых является длиной пути от ис­точника до данной точки.

Рисунок 10 – Первая узловая линия

Для любой точки Р на этой линии разность хода от S₁ до Р и от S₂ до Р равна полуволне

Сосчитав число гребней на длине каждого из двух рассматриваемых путей на рис. 10, мы убедимся, что РS₁=3λ и РS₂= λ, так что разность хода (т. е. разность длин путей) равна РS₁ ─ РS₂ = λ.

Выбрав любую другую точку на пер­вой узловой линии, мы получили бы такую же разность хода, т. е. λ. Таким образом, можно сказать, что первая узловая линия проходит через все точки Р, для которых разность хода от двух источ­ников равна λ, так что некоторый определенный гребень и неко­торая определенная впадина попадают в любую из точек этой узловой линии одновременно.

Вторая узловая линия может характеризоваться аналогичным образом.

Если Р является произвольной точкой второй узловой линии, то разность хода равна РS₁ ─ РS₂ = λ, в чем также можно убедиться, анализируя рис. 10. Продолжая эти рассуждения, можно прийти к уравнению описывающему n-ю узловую линию:

РS₁ ─ РS₂ = λ.

П ользуясь этим уравнением, можно строить любую n-ю узловую линию, находя точки пересечения дуг окружностей радиуса r, имеющих центр в S₁, с дугами окружностей радиуса , имеющих центр в S₂, что иллюстрирует рис.11.

Рисунок 11 – Построение узловой линии

Дуги окружностей с радиусами r и проведены вокруг

двух соответствующих точечных источников. Узловая линия проходит через точки пересечения этих дуг. На рисунке проведены первая и вторая узловые линии: п =1 и п =2

4 Длины волн, расстояния между источниками и углы

В волновой кювете можно измерить путь до любой точки на узловой линии. Используя при этом уравнение РS₁ ─ РS₂ = λ, можно определить и длину волны λ. Для таких измерений нет надоб­ности останавливать волны. Во время измерений отрезков РS₁ и РS₂ узловые линии остаются в покое.

И ногда бывает удобно и даже необходимо произвести измерения для точки Р, далеко отстоящей от S₁ и S₂. Но если непосредственно измерить два больших расстояния РS₁ и РS₂ и вычесть одно из другого для определения их малой разности, то точность окажется слишком малой. Необходимо поэтому искать более точный метод определения раз­ности хода.

Для любой точки Р, достаточно удаленной от источников, раз­ность хода РS₁ ─ РS₂ зависит от угла между РS₁ и d.

Рассмотрим на рис.12, а схему расположения двух источников S₁ и S₂ и точки Р, удаленной на большое расстояние по сравнению с расстоянием между источниками d.

Рисунок 12 – Разность хода AS₁ может быть выражена через расстояние между источниками d и углы. При большом удалении Р от источника AS₁=d·sinΘ

На прямой РS₁ отложен отрезок РА, равный расстоянию РS₂, так что углы 1 и 2 равны, причем

РS₁ ─ РS₂ =АS₁.

Чем дальше расположена точка Р, тем с большим правом можно рас­сматривать прямые РS₁ и РS₂ как параллельные. Ограничимся рассмотрением точек Р, настолько удаленных от S₁ и S₂, что прямые РS₁ и РS₂ можно считать практически параллельными. Этому усло­вию соответствует рис. 12, б. Поскольку углы 1 и 2 стали пря­мыми, треугольник АS₁S₂ является прямоугольным. Отсюда, по определению синуса угла,

Угол показан на рис. 12, б. Учитывая, что АS₁ есть разность хода, получаем

РS₁ ─ РS₂ =d

Это уравнение выражает раз­ность хода через расстояние между источниками и угол, определяющий направление, в котором находится точка Р по отношению к источникам излучения волн.

Например, при =90^о точка Р находится справа от источников на продолжении прямой, проходящей через оба источника. При =0^о точка Р находится против источников, на перпендикуляре, восстановленном из середины отрезка S₁S₂ , что хорошо видно на рис. 12, б.

Если точка Р находится на n-й узловой линии, то

РS₁ ─ РS₂ = λ.

Следовательно, λ= d , или = при условии, что Р достаточно удалено от S₁ и S₂ .

Между прочим, этот результат означает, что на достаточно боль­шом расстоянии от источников узловая линия не изменяет своего направления. Оно определяется углом .

Таким образом, вдали от источников узловая линия должна быть прямой. Если продолжить эти прямолинейные части узловых линий в сторону источников, то их продолжения сойдутся в средней точке между источниками.

В разделе 3 лабораторной работы было отмечено, что число узловых линий возрастает при уменьшении длины волны. Это легко увязать с последней формулой. Значение не может превышать единицу, значит, не может быть больше единицы. Наибольшее значение п, удовлетворяющее этому условию, есть число узловых линий по каждую сторону от средней линии. Это число зависит только от и увеличивается с уменьшением λ. Поэтому можно приближенно вычислить длину волны, просто сосчитав половину общего числа узловых линий.

Для точного вычисления λ следует определить направление п-й узловой линии, т.е. угол и вычислить λ из уравнения = .

В волновой кювете определяется легко, но это относится не ко всем видам волн. Рассмотрим метод непосредственного измерения без измерения самого угла .

Допустим, что точка Р на рис. 13 находится на п-й узловой линии вдали от источников S₁ и S₂ , так что прямые СР и S₁Р практически параллельны друг другу и обе перпендикулярны к АS₂. Поскольку средняя линия перпендикулярна к d, легко доказать, что = . Но , где =РС, а является расстоянием от Р до средней линии. Таким образом, для п-й узловой линии имеем

= = = или .

Рисунок 13 – Если точка Р достаточно удалена от источников, . Поскольку , то .

Кроме того, sin , откуда sin .

Рассмотрим на примере, насколько проста процедура определения λ. Пусть расстояние между источниками составляет 10 см. Выберем точку Р на третьей узловой линии и измерим ее расстояние от средней точки С, также ее расстояние х от средней линии.

Допустим, что получили = 80 см и х = 48 см. Отсюда = 0,6. Точность этого результата может быть проверена путем измерения значений и соответствующих значений х для других точек на третьей узловой линии. Если точки достаточно удалены, отношение остается равным 0,6.

Поскольку имеем дело с третьей узловой линией, то и при d = 10 см получаем

2,4 см.

Используя несколько узловых линий, можно произвести несколько измерений λ. Сходство результатов может служить проверкой правильности рассуждений и измерений.

5 Фаза

Два возбудителя водяных волн находятся в одинаковой фазе, если они каждый раз погружаются в воду одновременно, создавая гребни волн также одновременно. Но источники с одинаковым пе­риодом не всегда находятся в одинаковой фазе. Один из источников может погружаться в воду несколько позже другого, например с постоянным временем запаздывания t. Поскольку естественной единицей времени для каждого определенного периодического дви­жения служит его период Т, целесообразно измерять время запаз­дывания между погружениями источников S₁ и S₂ в долях р периода Т.

Итак, используем для характеристики запаздывания величину р= . Например, если источник S₁ погружается через интервалы в секунды, а источник S₂ каждый раз погружается на секунды позже, то р= .

Когда источники одинаковой частоты не погружаются одновре­менно, говорят, что они не совпадают по фазе, или имеют раз­ность фаз.

Дробь р характеризует отставание по фазе одного источника по отношению к другому. Отставаний, превышающих период, не бы­вает, так как отставание второго источника всегда измеряет­ся с момента последнего погружения первого источника, а после­довательные погружения происходят через период, т.е. равные интервалы времени Т.

Поэтому отставание по фазе, выраженное в долях периода не ^может превышать единицы; р всегда заключено между 0 и 1.

Воспользуемся теперь двумя точечными возбудителями волн, работающими таким образом, что S₂ отстает по фазе на р по срав­нению с S₁. Как будет в этом случае вы­глядеть интерференционная кар­тина?

Можно попытаться выяснить это графически, по­строив два семейства концентри­ческих гребней круговых волн, исходящих от двух источников. Как и на рис. 4, в каждом семействе гребни отстоят друг от друга на длину волны λ. Но на этот раз источники колебаний различа­ются по фазе, и радиусы r₁ и r₂ соответствующих гребней, исхо­дящих от двух источников, не равны (рис. 14). Радиусы запаздывающих гребней от S₂ меньше соответствующих радиу­сов гребней от S₁ на отрезок l, который относится к λ, как р : 1, т. е. l=рλ.

Рисунок 14 – Волны от двух точечных источников, Рисунок 15 – Расположение узловых

не совпадающих по фазе: S₂ отстает по фазе на р от линий при разности фаз р = 1/2

S₁. Разность радиусов соответственных гребней

двух систем волн равна

Например, если S₂ запаздывает на одну треть периода по отношению к S₁, то гребни, центр которых находится в S₂, меньше соответствующих кругов с центром в S₁ на одну треть длины волны.

В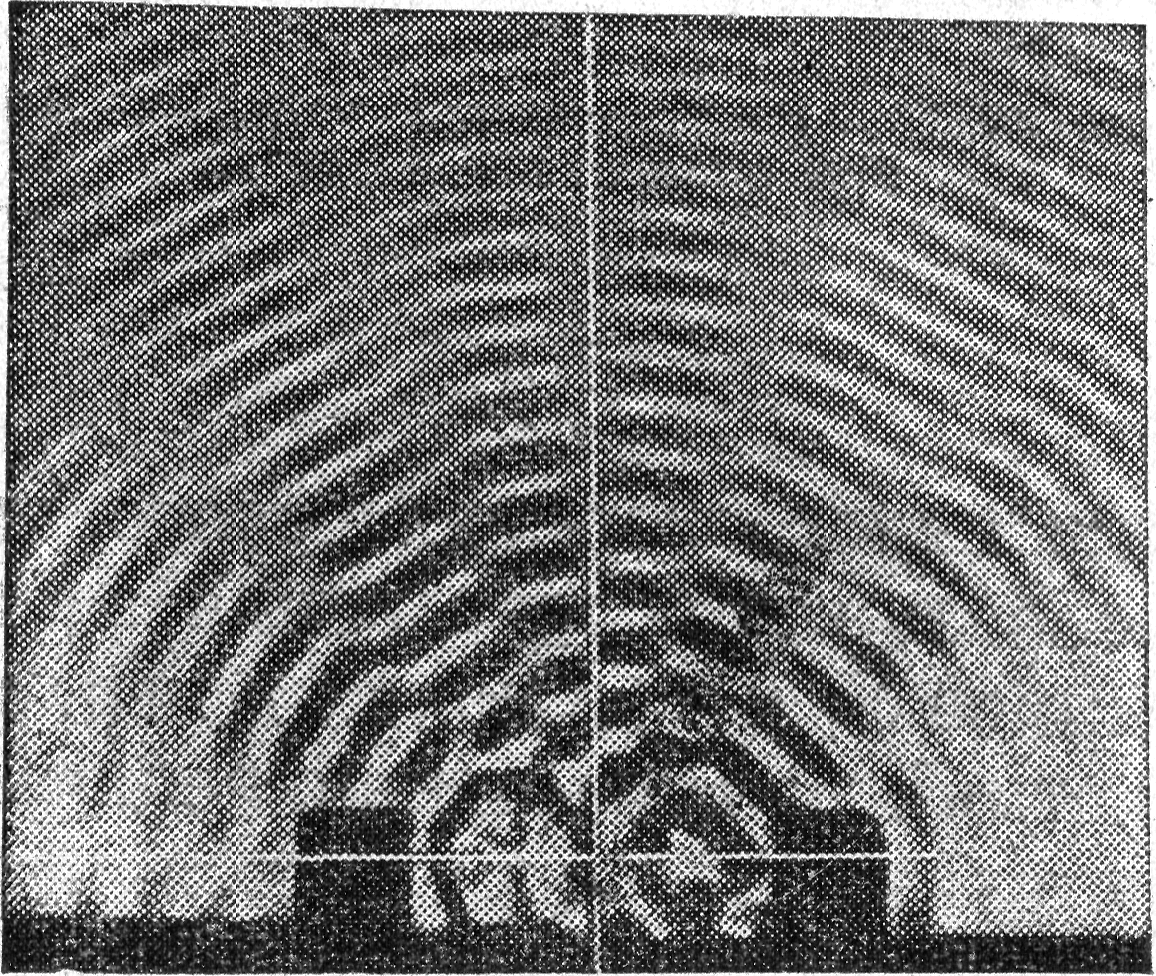 виде примера рассмотрим случай, когда один из источников отстает от другого на полпериода. В этом случае отрезок l равен полу­волне, а отставание по фазе составляет р= . Гребни волн для этого примера построены на рис. 15; там же проведены узловые линии, проходящие через точки пересечения гребней со впадинами. На рисунке видно, что расположение узловых линий отличается от картины, наблюдаемой при двух синфазных источниках. При том же отношении узловые линии находятся в том месте, где при синфазных источниках находились наиболее усиленные гребни, а наиболее уси­ленные гребни занимают места прежних узловых линий. Сравните рис. 15 с рис. 10. Для каждого из них , но на рис. 10 источники совпадают по фазе, а на рис. 15 имеется отставание по фазе р= .

Фотоснимок волновой картины при разности фаз источников р= приведен на рис. 16.

Рисунок 16 – Фотоснимок воновой картины во время действия двух источников с разностью фаз р =1/2

Можно видеть, например, что со сред­ней вертикальной прямой здесь совпадает узловая линия, тогда как на рис. 6 (и рис. 9) с ней совпадала линия наиболее усиленных гребней.

Таким образом, были рассмотрены примеры интерференционных картин для двух част­ных случаев разности фаз: р=0 и р= . Можно было бы выбрать любую разность фаз от 0 до 1, и в каждом случае интерференционная картина была бы разная.

С ерия фотоснимков на рис. 17 воспроиз­водит интерференционные картины на экране волновой кюветы для различных отставаний по фазе источника S₂. Изменение разности фаз сдвигает всю систему узловых линий в определенном направ­лении. По мере того как отставание по фазе источника S₂ увеличи­вается (от а к г), радиусы гребней волн системы S₂ отстают от ради­усов гребней системы S₁ на все возрастающий отрезок l=рλ. По­этому узловые линии все круче загибаются вокруг S₂, удаляясь от средней линии. Это и наблюдается на фотоснимках.

Рисунок 17 – Интерференция волн от двух точечных источников при возрастающем (от а к г) отставании по фазе р правого источника.

На фотоснимке а) источники синфазны (р =0).

На следующих сним­ках р возрастает, проходя через значение р =1/2 на снимке в).

Включив отрезок l=рλ в разность хода для любой точки узловой линии, получаем общую формулу разности хода для п-й узловой линии при произвольной разности фаз источников:

РS₁ ─ РS₂ = λ.

Отсюда (по причинам, рассмотренным в разделе 4) углы, опреде­ляющие направления прямолинейных концов узловых линий, выра­жаются формулой

= .

Эти уравнения легко понять, если учесть, что узловые линии опре­деляются пересечениями дуг радиуса r + λ с центром в S₁ с дугами радиуса r – рλ с центром в S₂. В такие точки пересечения гребень от одного источника всегда доходит одновременно со впадиной от другого (смотрите конец раздела 3).

При изменении запаздывания по фазе источника S₂ цепочки волн, состоящие из усиленных гребней и впадин, поворачиваются подобно узловым линиям. При увеличении этого запаздывания каждая цепочка волн отклоняется от S₁ и постепенно загибается вокруг S₂.

В качестве примера на рис. 18 построены гребни волн от двух источников, разделенных интервалом в 3λ.

Рисунок 18 - Ряд черных кружков изобра­жает линию удвоенных гребней при одина­ковых фазах источников S₁ и S₂. Белые кружки изображают удвоенные гребни при отставании S₂ по фазе. Запаздывающие греб­ни от S₂ изображены пунктирными дугами

Система сплошных кругов с центром в S₂ изображает гребни от S₂, которые получи­лись бы при совпадении фаз источников. Пунктирные же дуги с центром в S₂ обозначают гребни от S₂ при отставании S₂ по фазе. Обратите внимание на загибание удвоенных гребней в сторону S₂ при отставании S₂. В частности, при равенстве фаз по центральной вертикали про­ходит прямолинейная цепочка волн. При отставании источника S₂ эта цепочка смещается вправо, в сторону источника S₂. Все остальные цепочки волн при этом смещаются аналогичным образом.