
Лабораторная работа 7
Составление динамической модели простейшей акустической системы методом электроакустических аналогий
Цель работы: усвоение методики и развитие навыков выполнения начальных процедур анализа акустических систем
Методические указания к выполнению работы
Изучив материал по теме, выполнить задания, ответы на которые представить для отчета в письменном виде.
Введение
Источниками или излучателями звуковых волн являются механические колеблющиеся тела – струны, деки музыкальных инструментов, голосовые связки и любые вибрирующие поверхности.
Создаваемые
деформации сжатия и разряжения не
остаются в зоне образования, а
распространяются в окружающую среду с
определенной скоростью с0,
называемой скоростью
звука,
зависящей от плотности среды
![]() и модуля упругости
и модуля упругости
![]() =1,41·105
Н/м2).
Для воздушной среды с0=
=1,41·105
Н/м2).
Для воздушной среды с0=![]() ~340
м/с.
~340
м/с.
Механические колебательные системы, в которых элементы массы реализованы в в виде движущихся воздушных масс, а элементы гибкости – в виде замкнутых воздушных объемов, выделяются в особый класс акустических колебательных систем.
Акустическая колебательная система, как и простая механическая колебательная система, состоит из массы, гибкости и активного сопротивления, однако эти элементы сосредатачиваются в разных участках объема сосуда: своеобразной воздушной «пружиной» является воздух в полости сосуда; «массой» служит воздух, заполняющий горлышко резонатора; активное сопротивление образуется в результате потерь колебательной энергии вследствие излучения звука открытым концом горла.
В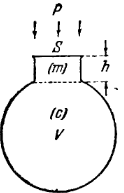 оздух
в любом сосуде с горлышком (например,
обыкновенной бутылки или флаконе)
образует акустическую колебательную
систему, а сам сосуд выполняет роль
резонатора Гельмгольца.
оздух
в любом сосуде с горлышком (например,
обыкновенной бутылки или флаконе)
образует акустическую колебательную
систему, а сам сосуд выполняет роль
резонатора Гельмгольца.
1 Резонатор Гельмгольца
Простейшая акустическая система с одной степенью свободы – так называемый резонатор Гельмгольца, представляет собой сосуд с коротким горлышком, заполненный воздухом.
При возбуждении резонатора звуковой волной воздух в горле резонатора колеблется, как поршень, а объем воздуха в полости резонатора (сосуде) создает необходимую упругость и обеспечивает возвращающую силу.
Таким образом, резонатор является колебательной системой с распределенными массой и упругостью.
Если размеры резонатора невелики по сравнению с длиной падающей волны (низкие частоты), то допустимо считать, что вся кинетическая энергия сосредоточена в слое воздуха, который движется в горле резонатора, а потенциальная энергия связана с упругой деформацией воздушного объема полости.
В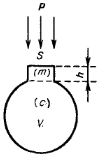
 этом предположении резонатор Гельмгольца
является колебательной системой с одной
степенью свободы, состоящей из
сосредоточенных параметров массой m
и упругостью с.
Активное сопротивление r
обусловлено трением воздуха о стенки
трубы и потерями колебательной энергии,
возникающими вследствие излучения
звука открытым концом.
этом предположении резонатор Гельмгольца
является колебательной системой с одной
степенью свободы, состоящей из
сосредоточенных параметров массой m
и упругостью с.
Активное сопротивление r
обусловлено трением воздуха о стенки
трубы и потерями колебательной энергии,
возникающими вследствие излучения
звука открытым концом.
Сосредоточенные параметры системы определяются следующим образом. Рассмотрим характер реакции, создаваемой воздухом, заключенным в объеме резонатора V, при колебаниях невесомого поршня площадью S. Атмосферное давление Ро.
Массу воздуха, движущегося в горле резонатора, можно определить как
![]() ,
,
где
![]() – высота горла,
– высота горла,
![]() –
сечение горла резонатора,
–
плотность воздуха.
–
сечение горла резонатора,
–
плотность воздуха.
Для определения гибкости воздушного объема в полости, представим, что воздушная пробка в горле смещается в сторону полости на величину х. Смещение невесомого поршня на расстояние х в сторону полости вызывает изменение объема на ΔV= – Sх и, следовательно, изменение давления в полости на величину ΔР.
Если
Ро
есть атмосферное давление, ΔР–
избыточное давление в полости и
![]() –
изменение объема V
воздуха в полости, то при адиабатическом
процессе
(адиабатический
процесс – это термодинамический процесс,
при котором система не получает теплоты
извне и не отдает ее. Быстропротекающие
процессы, например, распространение
звука, могут рассматриваться как
адиабатический процесс)
–
изменение объема V
воздуха в полости, то при адиабатическом
процессе
(адиабатический
процесс – это термодинамический процесс,
при котором система не получает теплоты
извне и не отдает ее. Быстропротекающие
процессы, например, распространение
звука, могут рассматриваться как
адиабатический процесс)
(Р0+ΔР)(V+ΔV)γ = Р0V γ ,
где γ = ср/сV – отношение удельных теплоемкостей, или показатель адиабаты.
Отсюда
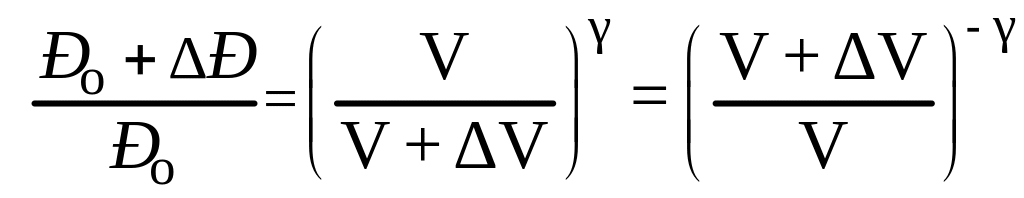
или

Если
колебания являются малыми, т.е.
![]() ,
то последующие члены биноминального
ряда можно отбросить. При этом, учитывая,
что ΔV=
–
Sх,
получаем
,
то последующие члены биноминального
ряда можно отбросить. При этом, учитывая,
что ΔV=
–
Sх,
получаем
![]() – избыточное,
или звуковое давление.
– избыточное,
или звуковое давление.
Тогда возвращающая сила или реакция воздуха, заключенного в полости,
 (1)
(1)
Пропорциональность
между
![]() и
и
![]() (по
аналогии с законом Гука) свидетельствует
об упругом характере реакции внутри
полости. Таким образом, замкнутый
воздушный объем акустической системы
подобен пружине механической колебательной
системы.
(по
аналогии с законом Гука) свидетельствует
об упругом характере реакции внутри
полости. Таким образом, замкнутый
воздушный объем акустической системы
подобен пружине механической колебательной
системы.
Из
(1) можно определить акустическую
гибкость
(![]() )
воздушного объема в полости как отношение
смещения
к
возвращающей упругой силе
)
воздушного объема в полости как отношение
смещения
к
возвращающей упругой силе
![]() :
:
 ,
(2)
,
(2)
где
![]() –
атмосферное давление;
–
атмосферное давление;
![]() –
объем резонатора;
–
сечение горла резонатора;
–
объем резонатора;
–
сечение горла резонатора;
![]() –
плотность воздуха;
–
плотность воздуха;
![]() –
скорость распространения звуковой
волны в воздухе, при температуре 20 оС,
равная 340 м/с,
–
скорость распространения звуковой
волны в воздухе, при температуре 20 оС,
равная 340 м/с,
![]() –
показатель адиабаты, равный 1,41
–
показатель адиабаты, равный 1,41
