4 Примеры изображения механических систем и их эквивалентные схемы

Пример 1. Груз, подвешенный на пружине и погруженный в сосуд с вязкой жидкостью, находится под действием силы, приложенной к нему (рис. 4).

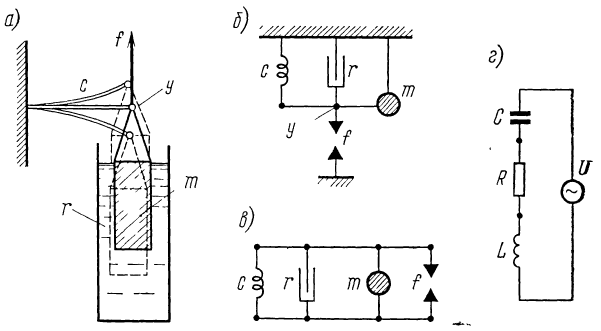
Рисунок 4 – Простейшая колебательная система из пружины, несущей массу,

погруженную в вязкую жидкость

Это пример механической системы с одной степенью свободы, которая описывается уравнением (6). Элементы этой системы соединены в узел: масса (m), гибкость пружины (с) и элемент трения (r), образуемый между поверхностью массы, вязкой жидкостью и неподвижными стенками сосуда, – все они имеют одинаковое перемещение концов.

Для изображения системы используем горизонтальную связку, к которой подсоединяем элементы гибкости, массы и трения одним концом, а вторые концы соединяем с изображением неподвижной опоры, как показано на рис 5,б. Таким же образом изображается и сила (f) (рис. 5, в).

Эквивалентная электрическая схема приведена на рис. 5, г.

Пример 2. Груз, подвешенный на пружине, к свободному концу которой приложена сила.

а) - груз на пружине, возбуждаемый через сво-бодный конец пружины,

б, в) - условное изображение системы;

г) - эквивалентная элек-трическая схема

Поскольку пружина считается идеальной (невесомой), силы, действующие на обоих концах при ее растяжении, всегда одинаковы, т.е. к массе приложена такая же сила, как и к свободному концу пружины. Таким образом, на оба элемента действует одна и та же сила – это пример соединения элементов цепочкой. Второй конец силы действует на неподвижную опору, а второй конец массы по условию всегда соединяется с неподвижной опорой.

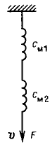
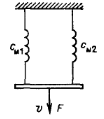
Пример 3. Система из двух масс и трех пружин с силой, приложенной к одной из пружин.

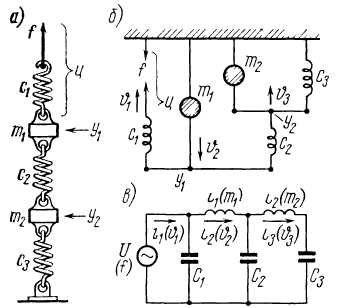
В этой системе имеется два узла: У₁ и У₂. Первый узел образован одним из концов с₁, массой m₁ и одним из концов с₂,

Второй узел образован массой m₂ , вторым концом с₂ и одним из концов с₃.

Имеется еще цепочка (u), обра-

зованная силой f, гибкостью с₁ и ос-тальной частью схемы. Узлы изображаются стяжками, а массы - двухполюсными элементами, вторые концы которых соединены с неподвижной опорой.

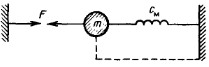
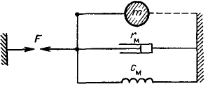
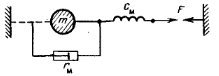
Пример 4. Система из двух масс и силы, действующей между ними.

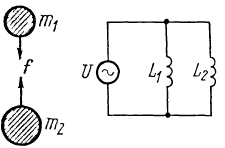
Такая система представляет собой соединение цепочкой двух масс и силы. Особенность ее в том, что второй конец силы приложен к одному из элементов рассматриваемой системы, а не к неподвижной опоре.

В эквивалентной схеме для примера 4 индуктивности, изображающие массы, соединены параллельно, и общий ток будет больше, чем протекающий через каждую индуктивность. Это соответствует уменьшению общей индуктивности в схеме и как бы уменьшению общей массы в механической системе, поскольку общий ток в этой схеме – это относительная скорость движения масс, которая, конечно, больше, чем скорость каждой из масс относительно неподвижной опоры.

ДОМАШНИЕ ЗАДАНИЯ

1. 1. Установите аналогию, существующую между уравнениями, описывающими колебания в электрических цепях и механических системах. Рассмотрение провести на примере линейных колебательных систем: механической с одной степенью свободы и электрического колебательного контура.

2. 2. Составьте таблицу аналогов, существующих между величинами, описывющими колебания в электрических цепях и механических системах (по образцу, приведенному в пункте 2.а).

Механическая величина	Электрическая величина
1.Смещение – х	заряд - q
2.Колебательная скорость
3.Сила
4.Масса
5.Гибкость
6.Активное механическое сопротивление
7.Ускорение
8.Полное механическое сопротивление
9.Инерциальное сопротивление
10.Упругое сопротивление
11.Собственная частота механической системы

2.а Механическая величина «х» это относительное смещение концов элемента упругости или элемента трения х = х₁ – х₂ .

В методе электромеханических аналогий, применяемым для анализа акустических систем, аналогом смещения является электрическая величина «заряд» q – электрический заряд, проходящий через поперечное сечение проводника колебательного контура при приложении внешней электро-движущей силы (эдс).

….

3. Установите аналогию в способах соединения механических и электрических элементов. Приведите формулу для расчета электрического аналога системы.

А) Б) В) Г)

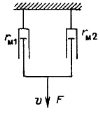
4. Индивидуальное задание: в соответствии с порядковым номером в журнале группы, для механических систем, изображенных на рис. 1…12, постройте схему электрического аналога.

1) 2)

3) 4)

5) 6)

7. 8)

9) 10)

11. 1 2)

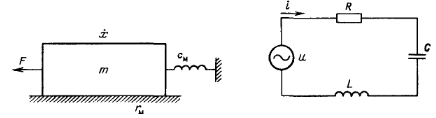
5 . Две массы m₁ и m₂ жестко связаны друг с другом и движутся вместе под действием силы F. Изобразить схему соединения механических элементов, построить схему электрического аналога и определить импеданс системы.

Ответ: Z=jω(m₁+m₂)

14