2 Электромеханическая аналогия

Колебательный контур составлен из последовательно соединенных индуктивности L, емкости C и омического сопротивления R, как показано на рис. 2. На процессы в контуре воздействует периодическая электродвижущая сила (ЭДС) .

Рисунок 2

Для такой цепи дифференциальное уравнение напряжений имеет вид:

,

где – ток в контуре.

Введя обозначение заряда конденсатора q = , получаем уравнение

, (16)

которое по форме ничем не отличается от уравнения (10) и имеет, соответственно, аналогичное решение.

В стационарном режиме ток в колебательной цепи равен

.

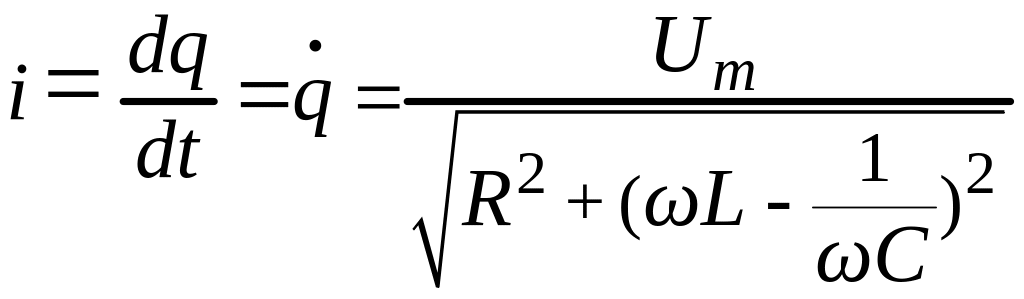Сравнение уравнений (10) и (16) позволяет составить таблицу электромеханических аналогов, т.е. взаимно аналогичных механических и электрических величин.

Механические величины Электрические величины

1. Переменные:

сила F (в Ньютонах) напряжение (ЭДС) U (в Вольтах)

скорость ( в м/с) ток ( в Амперах)

смещение (перемещение) (в м) заряд (в кулонах)

2) Параметры

масса m (кг) индуктивность L (Генри)

гибкость с (м/Н) емкость С (Фарада)

коэффициент трения r (Н·с/м) омическое (активное) сопротивление R (Ом)

3) Сопротивления

инерциальное индуктивное

упругое емкостное

полное z полное Z.

Совпадение математических описаний позволяет для синтеза механических колебательных систем, обладающих заданными частотными свойствами, рассматривать электрическую систему вместо механической. Это удобно потому, что в электротехнике на основании законов Кирхгофа и обобщенного на случай переменного тока закона Ома развит универсальный метод расчета электрических цепей.

Для расчетов необходимо составить динамическую модель колебательной системы. Динамической моделью называется изображение системы с помощью символов, установленных для каждого механического элемента – массы, гибкости или трения и отображающих их особенности, определить способы их сочетания друг с другом.

3 Механические двухполюсники и их соединения

Поскольку основные элементы механических систем соответствуют основным типам электрических двухполюсников (L, C, R), их называют простейшими механическими двухполюсниками, т.е. имеющими два конца.

Изображение элементов механических приведено на рис. 3.

Рисунок 3

1 – элемент трения; 2 – элемент гибкости;

3 – массивный элемент; 4 – сила и реакция опоры

Д вухполюсный характер основных элементов механических систем яснее всего обнаруживается в элементе гибкости, который можно представить в виде невесомой пружины.

Обозначим через х₁ и х₂ перемещения концов пружины. Тогда развиваемая пружиной упругая (возвращающая) сила . Так как в режиме стационарных колебаний все величины меняются во времени по закону , то и . Поэтому .

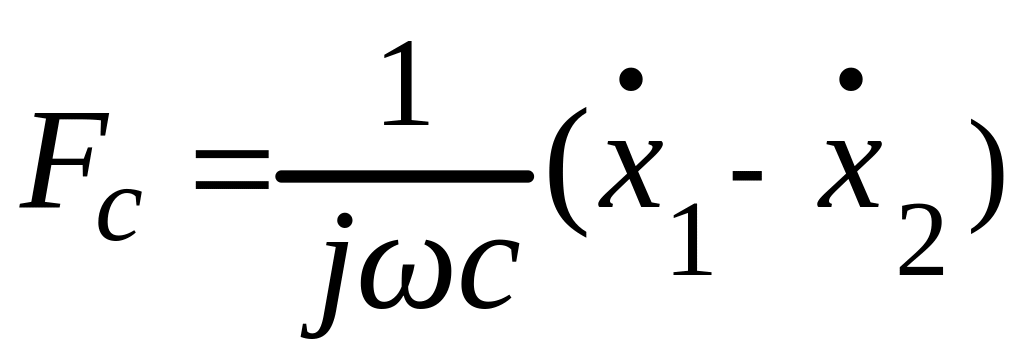Д вухполюсник, представляющий элемент трения (механическое активное сопротивление), изображают в виде невесомого цилиндра, внутри которого движется невесомый поршень с трением, пропорциональным относитель-ной скорости поршня и цилиндра. Если и - скорости цилиндра и поршня (т.е. концов двухполюсника), то диссипативная сила .

По отношению к элементам гибкости (пружина) и трения (поршень) предложенное на рис. 3 изображение естественно, опорой для них служат их вторые концы.

Почему массивный элемент (масса) представляется в таком виде?

Е сли мы хотим приложить к массивному элементу силу и сообщить ему ускорение, для этого необходима точка опоры. Такой неподвижной опорой – «вторым концом» – является корпус аппарата, фундамент, наконец, земля, масса которых велика по сравнению с той, которую мы двигаем. Эта точка всегда является закрепленной.

Масса – это мера инертности тел, т.е. . Так как в стационарном режиме , то предыдущее соотношение можно написать в виде .

Сила также изображается в виде двухполюсного элемента (см. рис. 3): один конец – собственно сила, приложенная к элементу, который приводим в движение, а второй – это реакция в сторону опоры.

М еханический элемент, характер сопротивления которого может быть произвольным, изображают в виде, показанном на рисунке.

Все рассмотренные соотношения для основных механических элементов имеют общую форму:

,

где может быть упругим ( ), активным ( ) или инерциальным ( ) сопротивлением (в последнем случае = 0, т.к. второй полюс закреплен связью с системой отсчета).

Сложные механические системы представляют в виде совокупности элементарных двухполюсников, соединенных друг с другом тем или иным способом.

Если все элементы в системе движутся с одинаковой скоростью, то их концы соединены вместе.

Такое соединение называется соединением в узел.

При соединении механических двухполюсников в узел развива-емые двухполюсниками усилия складываются, а относительные скорости концов одинаковы для всех элементов соединения:

и .

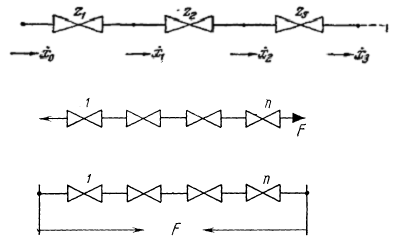Очевидно, что электрическим аналогом узла является последовательное соединение электрических двухполюсников, при котором ; .

Если через все элементы передается одна и та же сила, то элементы соединяются друг за другом. Такое соединение называется цепочкой.

Каждый из двухполюс-ников цепочки развивает одну и ту же силу. Это непосред-ственно вытекает из приме-нения закона равенства сил действия и противодействия, приложенных к точкам соединения концов смежных двухполюсников.

Так как электрическим аналогом силы является напряжение, а относительные скорости аналогичны токам, очевидно, что электрическим аналогом цепочки является параллельное соединение электрических двухполюсников, при котором: ; .