Лекции по ТММ2 / Лекция №3 16.09.2003

Created by SuhOFFF

П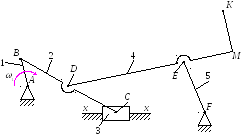лан ускорений механизма, как и план скоростей, не подобен самому механизму, и является совокупностью планов ускорений отдельных звеньев, построенных из одного полюса плана ускорений .

Заданы геометрические параметры всех звеньев и угловая скорость , которая является постоянной величиной.

Требуется определить ускорение точки .

Построение плана скоростей.

С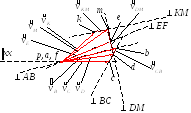корости точек и равны нулю, поэтому на плане скоростей точки и совпадают с полюсом плана скоростей .

Модуль скорости точки : . Линия действия вектора скорости точки : перпендикулярно звену .

Зададимся неким масштабным коэффициентом , и построим вектор на плане скоростей.

Скорость точки определяется из решения векторного уравнения , где - скорость точки ; - скорость точки , - скорость звена в его относительном вращении около точки . Вектор известен. Линия действия вектора : перпендикулярно звену . Линия действия вектора : параллельно направляющей .

Скорость точки определяется с помощью теоремы подобия и правила чтения букв. Правило чтения букв заключается в том, что порядок написания букв на плане скоростей или ускорений жёсткого звена должен в точности соответствовать порядку написания букв на самом звене. Из пропорции , можно определить длину отрезка и, построив его на плане скоростей, получить точку . Соединив полюс плана скоростей с точкой получим вектор скорости точки - .

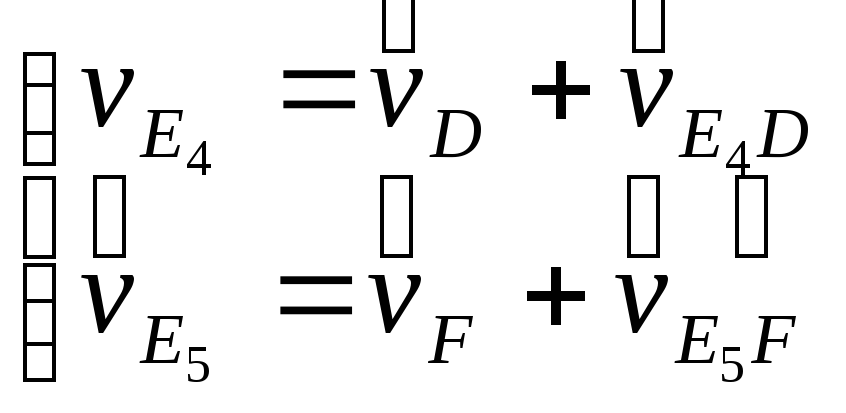Скорость точки определяется с помощью решения системы геометрических уравнений: , или .

Скорости точек и определяются с помощью теоремы подобия и правила чтения букв: , следовательно, ; , следовательно, , при этом .

Выводы:

1. Как видно из построений, план скоростей механизма не подобен самому механизму.

2. План скоростей даёт возможность найти скорость любой точки любого звена по величине и направлению.

Построение плана ускорений.

У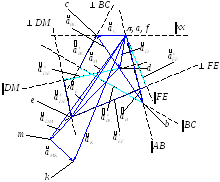скорения точек и равны нулю, поэтому соответствующие им точки и на плане ускорений совпадают с полюсом плана ускорений .

Ускорение точки можно найти с помощью решения векторного уравнения , где - ускорение точки , которое равно нулю; - ускорение звена в его относительном движении около точки . Ускорение звена можно представить в виде векторной суммы его нормального и тангенциального ускорений, то есть: . Тангенциальное ускорение звена равно нулю, поскольку его угловая скорость не меняется, поэтому ускорение точки равно нормальному ускорению звена , то есть Модуль нормального ускорения звена : . Линия действия вектора : параллельно звену . Направление вектора : к точке . Задавшись масштабным коэффициентом , строится вектор .

Скорость точки находится с помощью геометрического решения векторного уравнения: , где - ускорение точки ; - ускорение точки ; - нормальное ускорение звена ; - тангенциальное ускорение звена . Направление ускорения точки : параллельно направляющей . Ускорение точки известно. Модуль нормального ускорения звена : ; линия действия вектора : параллельно звену ; направление вектора : к точке . Линия действия вектора тангенциального ускорения звена : перпендикулярно звену .

Ускорение точки находится с помощью теоремы подобия и правила чтения букв: , следовательно, .

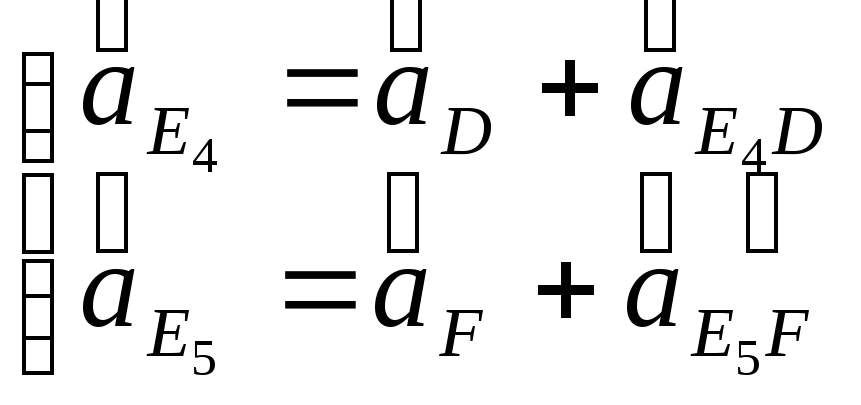Ускорение точки можно найти с помощью решения системы векторных уравнений: или .

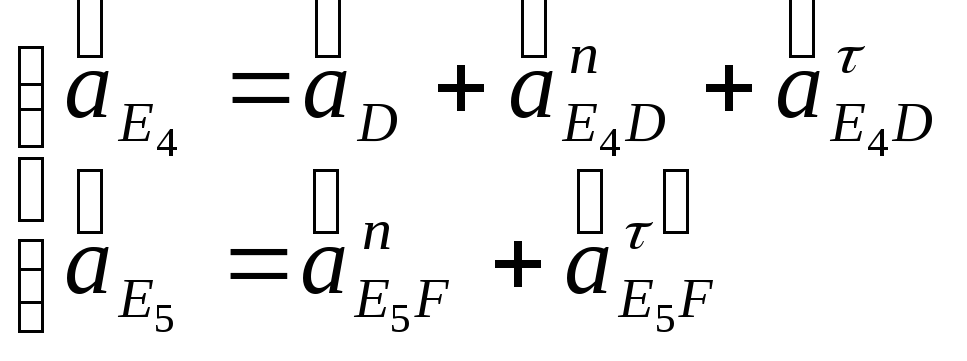Ускорения точек и определяются с помощью теоремы подобия и правила чтения букв: , следовательно, ; , следовательно, .

Теория машин и механизмов