15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
27.
28.
29.
30.
31.
32.
33.
ІІ.
Перевірити, що вектори
утворюють базис і розкласти вектор
за цим базисом.
|
|
|
|
|
1. |
|
|
|
|
2. |
|
|
|
|
3. |
|
|
|
|
4. |
|
|
|
|
5. |
|
|
|
|
6. |
|
|
|
|
7. |
|
|
|
|
8. |
|
|
|
|
9. |
|
|
|
|
10. |
|
|
|
|
11. |
|
|
|
|
12. |
|
|
|
|
13. |
|
|
|
|
14. |
|
|
|
|
15. |
|
|
|
|
16. |
|
|
|
|
17. |
|
|
|
|
18. |
|
|
|
|
19. |
|
|
|
|
20. |
|
|
|
|
21. |
|
|
|
|
22. |
|
|
|
|
23. |
|
|
|
|
24. |
|
|
|
|
25. |
|
|
|
|
26. |
|
|
|
|
27. |
|
|
|
|
28. |
|
|
|
|
29. |
|
|
|
|
30. |
|
|
|
|
31. |
|
|
|
|
32. |
|
|
|
|
33. |
|
|
|
|
Відповіді:
1.
,
2.
,
3.
,
4.
,
5.
,6.
,7.
,
8.
,
9.
,
10.
,
11.
,
12.
,
13.
,
14.
,
15.
,
16.
,
17.
,
18.
,
19.
,
20.
,
21.
,
22.
,
23.
,
24.
,
25.
,
26.
,
27.
,
28.
,
29.
,
30.
,
31.
,
32.
,
33.
.
Тема 3. Елементи аналітичної геометрії на площині Індивідуальне завдання 3
У
трикутнику АВС
задано координати вершини А
та векторів
і
.
Знайти:
а) координати вершин В і С;
б) кут при вершині А;
в) рівняння висоти, проведеної з вершини В;
г) рівняння медіани, проведеної з вершини В;
д) кут між медіаною і висотою, проведеними з вершини В;
е) довжину висоти, проведеної з вершини В.
Зробити рисунок.
Зразок виконання індивідуального завдання 3
У
трикутнику АВС
задано координати вершини А
(4;2) та векторів
і
.
Розв’язування.
а)
Оскільки
,
то для координат точки В
маємо співвідношення:
.
Аналогічно знаходимо координати точки С:
.
б)
Кут при вершині А
знайдемо як кут між векторами
і
(див.[1],
стор. 176). Маємо:
.
в)
Знайдемо рівняння сторони АС
трикутника, користуючись рівнянням
прямої, що проходить через дві задані
точки:
.
Вектор
нормалі до цієї прямої
можна взяти за напрямний вектор
в канонічному рівнянні висоти, проведеної
з вершини B(0;–1)
трикутника ABC:
отже
– рівняння висоти. Кутовий коефіцієнт
цієї прямої
.
г)
Знайдемо спочатку координати точки
,
як координати середини відрізку АС
(див.[1],
стор. 165):
;
.
Після цього запишемо рівняння прямої, що проходить через дві задані точки В і M (див.[1], стор. 193):
,
.
д)
З рівнянь висоти і медіани знаходимо
кутові коефіцієнти цих прямих. Маємо:
– кутовий коефіцієнт висоти BD;
– кутовий коефіцієнт медіани ВМ.
Кут між двома прямими знаходимо за
формулою
,
тому
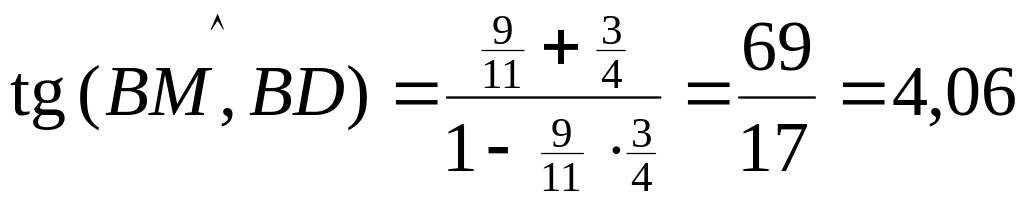, отже
.
е)
Щоб знайти довжину висоти ВD
як відстань від точки В
до прямої
,
запишемо нормальне рівняння прямої
(див.[1],
стор. 199):
.
Отже,
.
Y
C
M
A
В D Х
Варіанти завдань
А
|
А |
1. (5;2); (–3;8); (2;–8); 3. (10;2); (–2;–4); (2;8); 5. (0;2); (6;6); (–2;12); 7. (0;-2); (1;4); (-3;4); 9. (8;–3) ; (6;4); (–2;–2); 11. (–10;–2); (1;–1); (0;–6); 13. (3;2); (1;-2); (1;2); 15. (–1;–3); (–3;2); (–1;1); |
2. (2;4) ; (3;–1); (1;5); 4. (–3;5); (–2;0); (5;1); 6. (7;3); (1;0); (–4;–5); 8. (3;3); (1;2); (1;3); 10. (3;2); (3;0); (1;-2); 12. (–1;–3); (2;–1); (–6;5); 14. (1;9); (3;2); (–7;3); 16. (–3;–1) ; (–4;2); (2;–2); |
17. (–2;–1); (–5;6); (–4;1); |
18. (–1;–2); (4;5); (3;2); |
19. (1;–3) ; (–3;4); (5;10); |
20. (3;–1) ; (3;2); (5;2); |
21. (2;–1); (2;1); (–1;3); |
22. (–1;3); (5;7); (–2;–3); |
23. (–3;1); (–2;1); (6;7); |
24. (–2;1); (3;–1); (–2;–5); |
25. (–1;2); (4;–5); (5;8); |
26. (1;3); (–1;12); (–7;4); |
27. (3;1); (1;–1); (3;0); |
28. (2;1); (–1;9); (–3;–2); |
29. (1;2); (–4;5); (–5;8); |
30. (1;–2); (–4;5); (–5;–8); |
31. (3:1) ; (-1:-4); (-4:10); |
32. (0; 1); (6; 2); (-1;-1); |
33. (2: 2); (-3; 5); (-1; 2). |
|
Відповіді:
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1. |
(2;10) |
(7;-6) |
-1 |
|
|
0,6 |
2. |
(5;3) |
(3;9) |
-0,12 |
|
|
2,2 |
3. |
(8;-2) |
(12;10) |
-0,95 |
|
|
0,8 |
4. |
(-5;5) |
(2;6) |
-0,98 |
|
|
0,4 |
5. |
(6;8) |
(-2;14) |
0,57 |
|
|
8,4 |
6. |
(8;3) |
(3;-2) |
-0,6 |
|
|
1 |
7. |
(1;2) |
(-3;2) |
0,6 |
|
|
0,6 |
8. |
(4;5) |
(4;5) |
1 |
|
|
0,3 |
9. |
(14;1) |
(6;-5) |
-1 |
|
|
5,6 |
10. |
(6;2) |
(4;0) |
0,5 |
|
|
3 |
11. |
(-9;-3) |
(-10;-8) |
0,7 |
|
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
12. |
(1;-4) |
(-7;2) |
-1 |
|
|
0,5 |
13. |
(4;0) |
(4;4) |
-0,6 |
|
|
1,68 |
14. |
(4;11) |
(-6;12) |
-0,5 |
|
|
9,1 |
15. |
(-4;-1) |
(-2;-2) |
1 |
|
|
3 |
16. |
(-7;1) |
(-1;-3) |
-1 |
|
|
1,4 |
17. |
(-7;5) |
(-8;0) |
0,8 |
|
|
6,2 |
18. |
(3;3) |
(2;0) |
1 |
|
|
2,1 |
19. |
(-2;1) |
(6;7) |
0,5 |
|
|
5 |
20. |
(6;1) |
(8;1) |
1 |
|
|
0,8 |
21. |
(4;0) |
(1;2) |
0,1 |
|
|
1,4 |
22. |
(4;10) |
(-3;0) |
-1 |
|
|
0,3 |
23. |
(-5;2) |
(3;8) |
-0,2 |
|
|
0,2 |
24. |
(1;0) |
(-4;-4) |
-0,1 |
|
|
3,4 |
25. |
(3;-3) |
(4;10) |
-0,3 |
|
|
5,7 |
26. |
(0;15) |
(-6;7) |
0,6 |
|
|
9,6 |
27. |
(4;0) |
(6;1) |
0,7 |
|
|
1 |
28. |
(1;10) |
(-1;-1) |
0,5 |
|
|
8,7 |
29. |
(-3;7) |
(-4;10) |
1 |
|
|
0,4 |
30. |
(-3;3) |
(-4;11) |
-0,3 |
|
|
2,7 |
31. |
(2;-3) |
(-1;2) |
-0,8 |
|
|
3,4 |
32. |
(6;3) |
(-1;0) |
-0,9 |
|
|
2,1 |
33. |
(-1;7) |
(1;4) |
1 |
|
|
0,5 |
