I плоская волна

Согласно гипотезе Голицына Б.Б. – количество поглощаемой в пути энергии, пропорционально толщине слоя (dx) и количеству входящей в него энергии – (I).

Пусть имеем:

I-количество энергии подводимой к слою;

dI- количество энергии поглощаемой средой;

dx- толщина слоя;

- коэффициент, характеризующий затухание энергии в среде (пути);

Тогда можно записать

; (-) – энергия поглощается;

Далее интегрируя, получим:

Рассмотрим распространение плоской волны.

Возьмем два сечения 1 и 2 на расстоянии Z₁ b Z₂ соответственно.

Тогда для сечения 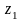и _имеем:

;

;

;

Для вязкой среды, где сопротивление вязкой среды пропорционально скорости колебаний, а энергия колебаний пропорциональна квадрату амплитуды, тогда:

;

где с-коэффициент вязкого сопротивления;

а- амплитуда;

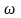- частота.

;

; откуда имеем

Случай распространения кольцевых волн.

I- количество энергии проходящей через единицу длины окружности радиусом r описанной окружности вокруг источника колебаний.

I’- количество энергии проходящей через единицу длины окружности радиусом r+dr описанной окружности вокруг источника колебаний.

Если в пути энергия не поглощается, то количество энергии проходящее через единицу длины окружности на радиусе r+dr равно I’, тогда:

или

;

или с определенной погрешностью

Но теперь надо учесть, что согласно гипотезе Голицына энергия в пути поглощается толщине слоя и количеству подаваемой в него энергии: то есть . Тогда полное поглощение энергии с переходом от окружности с радиусом r до r+dr будет:

или:

Интегрируя:

;

Запишем:

;

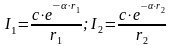или

или

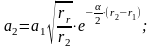
III сферическая волна.

Частота колебаний,Гц	Коэфф. Затухания колебаний 1/см	Минимальная амплитуда колеб. Бетонной смеси, см
100	0,04	0,004
150	0,055	0,003
200	0,07	0,002
300	0,09	0,0015

Виброамортизаторы

Для низких частот (260) Гц основным показателем вибрации является виброперемещение.

Для Гц и выше (82000) – виброскорость.

- децибел (относительно единица).

Методы снижения вибрации

В технике широко распространены объекты, движущиеся с большими ускорениями или подвергающиеся вибрации и ударным воздействиям. К таким объектам можно отнести и вибрационные и виброударные площадки для изготовления бетонных и железобетонных изделий. В результате отдельные узлы на таких объектах, или механизмы испытывают большие перегрузки, грозящие выходом их из строя. Кроме того, оказывают вредное влияние на организм операторов , обслуживающих такое оборудование.

Для уменьшения этих перегрузок узлы и механизмы крепятся к корпусу движущегося объекта не жестко, а с помощью специальных технических устройств — амортизаторов, которые, осуществляя управляющее воздействие на защищаемый объект, снижают неблагоприятное влияние внешних факторов.

Существует много работ, посвященных теории амортизационных систем. Подробное изложение теории виброзащитных и противоударных систем содержится в работе М. 3. Коловского [2] , К. В. Фролова и Ф. А. Фурмана [3], А. Ю. Ишлинского [6, 7] а также в справочнике [5].

А. Ю. Ишлинским [6, 7] показано, что амортизаторы целесообразно применять лишь в том случае, когда путь разгона или торможения объекта, содержащего амортизируемое тело, не больше хода амортизации. А˂▲, где ▲- статическая осадка акмортизатора. (максимального отклонения амортизируемого тела относительно основания). Это, по существу, означает, что амортизаторы обеспечивают эффективную защиту только от ударных внешних воздействий и высокочастотных вибраций. Под ударом понимается кратковременное внешнее воздействие большой интенсивности, а под вибрацией — продолжительное действие возмущающего фактора (силы при динамическом внешнем воздействии или ускорения движения основания при кинематическом), часто изменяющегося как по величине, так и по направлению. Эффективность функционирования противоударных амортизаторов определяется в основном механическими характеристиками свободных колебаний амортизируемого тела (переходного процесса), а качество виброзащитных устройств — характеристиками установившихся колебаний. Это обстоятельство обусловливает ряд отличительных особенностей в методике решения задач оптимальной амортизации в случае ударного внешнего воздействия и вибрации.

Рассматрим виброзащитные системы, основными элементами которых являются упругие амортизаторы (3 на рис. 1), устанавливаемые между основанием I и амортизируемым объектом 2. Виброзащитные системы такого рода могут быть разделены на две группы. К первой группе относятся активные системы, в которых внешние, переменные во времени силы, приложены к амортизируемому объекту, а задачей упругих амортизаторов является защита основания от действия этих сил.

В пассивных системах, составляющих вторую группу, динамические воздействия вызываются движением основания с переменным ускорением. Задачей амортизаторов в таких системах является защита амортизируемого объекта от этих динамических воздействий.

На рис. 2 приведены принципиальные схемы простейших виброзащитных систем с одной степенью свободы, активной (рис. 2, а) и пассивной (рис. 2, б). В обоих случаях положение амортизируемого объекта относительно основания определяется координатой и. Начало отсчета выбирается таким образом, чтобы в положении статического равновесия и равнялось нулю. Используя второй закон Ньютона, составим уравнения движения амортизируемого объекта, имеющего массу m. Для активной системы получим:

(1)

где и — ускорение объекта, — U — реакция упругого амортизатора,

Q(t) — внешняя сила, приложенная к объекту.

2) Активная 1) Пассивная

Амортизация от предмета

Амортизация предмета (человека)

б) Демпфирование:

С нижает вибрацию только в зоне резонанса.

Для пассивной системы

(2)

Здесь — закон движения основания, а 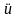— относительное ускорение объекта.

В активной системе на основание передается сила U. Основная задача виброзащитной системы — это уменьшение динамической (переменной) составляющей этой силы. В пассивной системе, как это видно из уравнения (2), реакция амортизатора — U представляет собой силу, приложенную к амортизируемому объекту; поэтому и здесь виброзащитная система должна уменьшать динамическую составляющую этой силы.

Реакция идеально упругого амортизатора является функцией его деформации и. В реальных амортизаторах деформация всегда сопровождается рассеянием энергии, вызванным либо внутренним трением в деформируемом материале, либо применением специальных демпфирующих устройств. Если учитывать демпфирование, то оказывается, что величина реакции зави­сит не только от деформации, но и от ее производных по времени. В большинстве случаев при проведении практических расчетов достаточно ограничиться учетом только первой производной, то есть принять, что

(3)

При этом уравнения (1) и (2) могут быть записаны в следующей общей форме:

(4),

причем в случае пассивной системы:

(5)

Поведение системы (4) определяется характером внешнего воздействия («вынуждающей силы») Q(t). В теории виброзащитных систем рассматриваются два класса внешних воздействий. К первому классу относятся вибрационные воздействия, классическим примером которых может служить гармоническая вынуждающая сила:

Q(t)= (6)

Вибрационные воздействия, с которыми приходится иметь дело при исследовании современных виброзащитных систем, обычно являются полпгармоническами, то есть могут быть представлены в виде суммы конечного или бесконечного числа гармонических компонент:

(7)

Второй класс вынуждающих сил, рассматриваемых в теории виброзащитных систем, образуют ударные воздействия. Классическим примером ударного воздействия может служить силовой импульс — воздействие бесконечно большой силы в течение бесконечно малого интервала времени, вызывающее изменение количества движения системы на конечную вели­чину. Такой «мгновенный» удар является, разумеется, идеализацией, которая далеко не всегда пригодна для описания реальных ударных воздействий. В теории виброзащитных систем термин «удар» имеет более широкий смысл: ударом называется обычно кратковременное воздействие на систему сравнительно больших внешних сил. Ударное воздействие характеризуется законом изменения 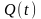; некоторые возможные формы этой зависимости показаны на рис. 3. Во всех случаях (8)

Интервал времени т, в течение которого прикладывается к системе ударное воздействие, называется длительностью удара; зависимость Q(t) часто называют формой удара.

Классическая линейная теория виброзащитных систем исходит из возможности замены реального упругого амортизатора его идеализированной моделью — линейным амортизатором. Напомним основные положения и выводы этой теории.

Предполагается, что динамическая составляющая реакции амортизатора складывается из упругой силы, пропорциональной деформации, и силы сопротивления, пропорциональной скорости деформации:

(9)

Коэффициент с называется жесткостью амортизатора, b —коэффициентом демпфирования. Подставляя (9) в уравнение (4), получаем:

(10)

Вводя обозначения:

приводим уравнение (10) к следующей форме:

(11)

Общее решение этого уравнения, как известно, складывается из общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. При начальных условиях:

t=0, u=u₀,

общее решение уравнения (11) имеет такой вид [8]:

, (12)

где

Исследуя поведение виброзащитной системы при вибрационном воздействии, обычно ограничиваются определением установившегося движения, соответствующего достаточно большим значениям t. Поскольку при наличии демпфирования (n> 0) свободные колебания, соответствующие первому слагаемому в выражении (12), затухают, установившееся движение оказывается не зависящим от начальных условий и полностью определяется видом вибрационного воздействия. При гармоническом вибрационном воздействии (6) установившиеся вынужденные колебания также оказываются гармоническими. При этом:

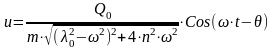, (13)

где — сдвиг по фазе между колебаниями и вибрационным воздействием, определяющийся по формуле:

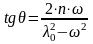(14)

Подставляя (13) в формулу (9), можно определить усилие, передаваемое амортизатором при вибрационном воздействии:

(15)

Где

Коэффициент К = U/Q_о или

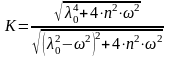(16)

представляет собой отношение амплитуды гармонической силы U к амплитуде гармонического вибрационного воздействия и называется обычно коэффициентом динамичности. Этот коэффициент характеризует качество виброзащитной системы. Если К< 1, виброзащитная система эффективна, она снижает амплитуду вибрационного воздействия, при К> 1 применение упругого амортизатора становится нецелесообразным. В самом деле, если крепить объект к основанию жестко, без амортизаторов, то динамическое воздействие, передаваемое таким жестким креплением, будет, очевидно, равно Q(t). Таким образом, для жесткого соединения К=1.

Вводя в формулу (16) безразмерные параметры:

,

получаем

(17)

На рис. 4 приведены графики зависимости К (z) при разных значениях v. Из этих графиков видно, что независимо от значения v, при коэффициент динамичности меньше единицы, причем его величина тем меньше, чем меньше v.

При полигармоническом вибрационном воздействии вида (7) вынужденные колебания являются полигармоническими. Используя принцип суперпозиции, получаем

(18)

где

(19)

Аналогично, для силы U имеем:

(20)

причем:

(21)

Очевидно, что если для всех i выполняется условие , то амплитуда каждой из гармонических составляющих силы U меньше, чем амплитуда соответствующей гармоники вибрационного воздействия, и виброзащитная система окажется эффективной.

При ударном воздействии обычно исследуется движение, соответствующее нулевым начальным условиям:

(22)

Подставляя это выражение в формулу (9), получаем:

(23)

Качество виброзащитной системы при заданном ударном воздействии может быть оценено коэффициентом динамичности при ударе Ку, равным отношению максимального значения усилия U к максимальному значению Q

24

В линейной теории рассматриваются обычно виброзащитные системы со слабым демпфированием; в таких системах при исследовании удара можно с достаточной степенью точности принять n=0. При этом формулы (22) и (23) принимают такой вид:

(25)

(26)

(27)

предполагая, что n = 0. Из выражения (26), произведя интегрирование, получим:

(28)

(29)

Первое из этих выражений достигает максимума при t=t₁.= . Этот максимум, равный 2Q_m, может быть достигнут только в том случае, если

(30)

Если же

(31)

то максимальное значение U определяется по формуле (29):

(32).

Оно достигается при

(33)

Таким образом,

(34)

Для того, чтобы амортизатор уменьшал ударное воздействие, должно быть К_у<1, что обеспечивается при

(35)

Этот вывод остается справедливым для ударного воздействия любой формы. В самом деле, определим значения u( ) и для удара произвольной формы. Дифференцируя выражение (25), находим

Таким образом,

Найдем значение Ку для удара «прямоугольной» формы

(36)

(37)

При t> в системе происходят свободные колебания, амплитуда которых, равная максимальной деформации амортизатора, определяется следующим способом:

При отсутствии демпфирования максимальное усилие соответствует максимальной деформации. Поэтому

При выполнении условия (35) ядра интегралов (36) и (37) положительны при всех значениях t’. Поэтому, если

Учитывая эти неравенства, получаем

Таким образом, при заданных значениях Q_m и величина максимального усилия, передаваемого амортизатором, оказывается наибольшей, если удар имеет прямоугольную форму. Отсюда, в частности, следует, что при выполнении условия (35) К_у окажется меньше единицы, какова бы ни была форма удара.

Учет демпфирования не изменяет сколько-нибудь существенно полученных результатов. При ударе прямоугольной формы для усилия получаем:

при t> (40)

Если отношение n/ является малым. То, пренебрегая членами порядка 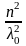, можно получить следующие выражения для коэффициента динамичности при ударе:

(41)

Исследование поведения линейной системы с одной степенью свободы при вибрационном и ударном воздействии позволяет сделать следующие выводы:

1. Уменьшение жесткости амортизатора, а следовательно, и собственной частоты системы приводит к ухудшению ее виброзащитных свойств. Для того, чтобы линейная система защищала от вибрационных воздействий, должно выполняться условие:

где w_min - наименьшая из частот гармонических компонент, имеющихся в вибрационном воздействии. Для защиты от ударных воздействий достаточно, чтобы выполнялось условие (35).

2. Если выполнено условие (42), то увеличение демпфирования может только ухудшить вибразащитные свойства системы. С этой точки зрения введение сильного демпфирования является нежелательным; слабое демпфирование, обеспечивающее затухание свободных колебаний, возникающих в системе при ударных воздействиях, оказывается вполне достаточным для виброзащитных систем.

Эти выводы, составляющие основу линейной теории виброзащитных систем, могут быть распространены и на системы с несколькими степенями свободы. ,Основные рекомендации (желательность снижения собственных частот системы и нецелесообразность введения в систему сильного демпфирования) сохраняют силу и в этом случае.

Казалось бы линейная теория предлагает универсальный метод эффективного решения задач, связанных с защитой от вибраций и ударов: необходимо создавать достаточно мягкие линейные системы со слабым демпфированием. Однако опыт проектирования и эксплуатации реальных виброзащитных систем показал, что в большинстве случаев этот метод не приводит к желаемым результатам. Более того, в последние годы развитие конструкций виброзащитных систем пошло в направлении, противоречащем рекомендациям линейной теории. Появились и получили широкое применение жесткие и сильно демпфированные системы. Причиной такого несоответствия является ограниченность линейной теории, ее непригодность для описания ряда явлений, происходящих в виброзашитных системах.

Ограниченность линейной теории связана в первую очередь с ограниченностью размеров впброзащитных устройств. Любой реальный амортизатор может иметь линейную упругую характеристику лишь в некоторой области значений деформации, называемой обычно областью линейности, в любой реальной виброзащитной системе должны существовать «ограничители хода», устанавливающие предельно возможные размеры области линейности. Естественно, что использование линейной теории для анализа виброзащитной системы возможно лишь в том случае, если при заданных воздействиях деформации амортизаторов не выходят за пределы области линейности. Однако во многих задачах выполнение этого условия оказывается практически невозможным.

Рассмотрим следующий пример. Пусть мы желаем защитить объект от удара, вызванного движением основания с ускорением м/сек² в течение времени . Максимальное ускорение объекта, равное, очевидно, отношению U_max/m, не должно превышать 50 м/сек². Попытаемся применить для защиты линейную систему без демпфирования. Поскольку в рассматриваемом случае , получаем:

Отсюда из выражения (34) находим

Найдем величину наибольшей деформации такого амортизатора при заданном ударном воздействии. Используя формулу (32), получаем

м

Такая величина «свободного хода», разумеется, практически неприемлема; поставленная задача оказалась невыполнимой, во всяком случае при использовании амортизаторов с линейной характеристикой.

Не менее существенными оказываются размерные (габаритные») ограничения при вибрационных воздействиях Наиболее четко их влияние сказывается в тех случаях, когда частота вибрационного воздействия оказывается настолько низкой, что не удается избежать резонанса. При формула (13) дает

(43)

Для того чтобы ограничить максимальную амплитуду при резонансе, не допустить выхода системы за пределы линейной области, приходится увеличивать коэффициент v, то есть вводить более сильное демпфирование.

Однако влияние габаритных ограничений этим не исчерпывается. Они приводят к возможности возникновении ряда явлений, носящих ярко выраженный «нелинейный характер» и не обнаруживаемых при линейном анализе. Дело в том, что в силу ограниченности линейного участка упругой характеристики становится уже неправомерным предположение о не­зависимости установившегося движения от начальных условий; в реальных виброзащитных системах оказывается возможным существование нескольких установившихся колебательных режимов при одном и том же вибрационном воздействии.

При колебаниях, выходящих за пределы области линейности, виброзащитная система уже не защищает от вибрационных воздействий; поэтому во всякой удовлетворительно работающей системе возможность возникновения таких колебаний должна быть исключена. Это достигается в первую очередь за счет увеличения демпфирования. Вместе с тем, как мы видели, с россом демпфирования ухудшаются виброзащитные свойства системы при высокочастотных воздействиях; в связи в этим возникает задача о выборе оптимального демпфирования, решение которой становится одной из главных проблем теории виброзащитных систем.

В свою очередь введение интенсивного демпфирования является еще одной причиной нелинейности реальных виброзащитных систем. Практически сложно осуществить достаточно эффективные демпферы, сила трения в которых была бы пропорциональна скорости; значительно более простыми в конструктивном отношении оказываются нелинейные демпферы, например, использующие сухое трение.

Сухое трение существенно ухудшает виброзащитные свойства системы при высокочастотном вибрационном воздействии. Улучшение виброзащитных свойств может быть достигнуто изменением конструкции амортизатора с сухим трением. В амортизаторах, схематически изображенных на рис.5, демпфер сухого трения соединяется с объектом через дополнительный упругий элемент.

Чем выше уровень, вибрационных и ударных воздействий, тем сильнее сказываются перечисленные выше обстоятельства, приводящие к ограни-ченности линейной теории. Именно поэтому в последнее время с появлением новых интенсивных источников вибраций и ударов стала особенно актуальной необходимость исследования виброзащитных систем нелинейными методами.

в) Динамические гасители:

Подбираем и так, чтобы колебался только шарик. Гашение здесь только в одной частоте.

1. Установка антивибратора

обвести рисунки