МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Вычислительной техники и защиты информации»
Расчётно-графическая работа
По дисциплине:
«Теория Автоматов»
«Часть 1»
Выполнил:
студент группы ВМ-218
Проверил:
профессор кафедры ВТ и ЗИ
Фрид А.И.
Уфа 2004
Оглавление
ОГЛАВЛЕНИЕ 2
ИСХОДНЫЕ ДАННЫЕ 3
ПЕРЕХОД ОТ ПРАВОЛИНЕЙНОЙ ГРАММАТИКИ К АВТОМАТНОЙ 4
ПОСТРОЕНИЕ НЕДЕТЕРМИНИРОВАННОГО КОНЕЧНОГО АВТОМАТА 4
ГРАФ МИНИМАЛЬНОГО АВТОМАТА 7
СЕТИ ПЕТРИ 8
Синтез распознающего автомата.
ЦЕЛЬ РАБОТЫ: изучение способов задания языков, грамматиками, распознающими автоматами, сетями Петри и построение конечного автомата распознающего заданный язык.
Исходные данные
|
А |
Б |
В |
Г |
Д |
Е |
Ж |
З |
И |
Й |
К |
Л |
М |
Н |
О |
П |
|
x1 |
x5 |
x2 |
x4 |
x6 |
x6 |
x4 |
x3 |
x3 |
x0 |
x7 |
x0 |
x3 |
x7 |
x4 |
x5 |
|
Р |
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ь |
Ы |
Э |
Ю |
Я |
_ |
|
x0 |
x4 |
x5 |
x7 |
x2 |
x5 |
x1 |
x2 |
x2 |
x0 |
x6 |
x1 |
x1 |
x3 |
x7 |
x5 |
|
Ci |
c1 |
c2 |
c3 |
c4 |
c5 |
c6 |
c7 |
c8 |
c9 |
c10 |
c11 |
c12 |
c13 |
c14 |
c15 |
c16 |
c17 |
c18 |
|
Si |
С |
А |
Р |
Б |
А |
Ш |
Е |
В |
_ |
К |
И |
Р |
И |
Л |
Л |
_ |
В |
Я |
|
xi |
x4 |
x1 |
x0 |
x5 |
x1 |
x2 |
x6 |
x2 |
x5 |
x7 |
x3 |
x0 |
x3 |
x0 |
x0 |
x5 |
x2 |
x7 |
Задана грамматика G = (N,T,P,S), где N = {S, A, B, C, D, F} T={c1, c2,…, c18} P: S→c1c2c3A | c1c4c5B | c6C |c7F; A→c8D | c9; B→c8E | c9; C→ c8E | c9; D→c10S | c11; E→c10S | c11; F→c12c13c14c15 | c16c13c14c15 | c17c18c15. S.
Данная грамматика является праволинейной, она приводится к следующему виду:
S→x4x1x0A | x4x5x1B | x2C | x6F, A→x2D | x5; B→x2E | x5; C→x2E | x5; D→x7S | x3; E→ x7S | x3; F→x0x3x0x0 | x5x3x0x0 | x2x7x0.
Окончательно терминальный словарь T’ имеет вид T’={x0,…,x7}
Переход от праволинейной грамматики к автоматной
Переход от праволинейной грамматики к автоматной осуществляется за счёт расширения нетерминального словаря.
S→x4S1, S1→x1S2, S2→x0A; S→x4S3, S3→x5S4, S4→z1B; S→x2C, S→x6F. A→x2D, A→x5; B→x2E, B→x5; C→x2E, C→x5; D→x7S, D→ x3; E→x7S, E→x3; F→x0F1, F1→x3F2,F2→x0F3,F3→x0; F→x5F4, F4→x3F5, F5→x0F6, F6→x0; F→x2F7, F7→x7F8, F8→x0.
Новый полученный недетерминированный словарь автоматной грамматики включает в себя следующие символы:
N’={S, S1, S2, S3, S4, A, B, C, D, E, F, F1, F2, F3, F4, F5, F6, F7, F8}
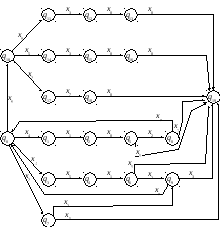
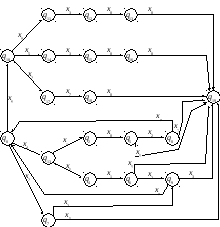
Построение недетерминированного конечного автомата
|
S |
S1 |
S2 |
S3 |
S4 |
A |
B |
C |
D |
E |
F |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
- |
|
q0 |
q1 |
q2 |
q3 |
q4 |
q5 |
q6 |
q7 |
q8 |
q9 |
q10 |
q11 |
q12 |
q13 |
q14 |
q15 |
q16 |
q17 |
q18 |
q19 |
q0 – начальное состояние q19 – конечное состояние
|
q |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
q0 |
|
|
q7 |
|
{q1,q3} |
|
q10 |
|
|
q1 |
|
q2 |
|
|
|
|
|
|
|
q2 |
q5 |
|
|
|
|
|
|
|
|
q3 |
|
|
|
|
|
q4 |
|
|
|
q4 |
|
q6 |
|
|
|
|
|
|
|
q5 |
|
|
q8 |
|
|
q19 |
|
|
|
q6 |
|
|
q9 |
|
|
q19 |
|
|
|
q7 |
|
|
q9 |
|
|
q19 |
|
|
|
q8 |
|
|
|
q19 |
|
|
|
q0 |
|
q9 |
|
|
|
q19 |
|
|
|
q0 |
|
q10 |
q11 |
|
q17 |
|
|
q14 |
|
|
|
q11 |
|
|
|
q12 |
|
|
|
|
|
q12 |
q13 |
|
|
|
|
|
|
|
|
q13 |
q19 |
|
|
|
|
|
|
|
|
q14 |
|
|
|
q15 |
|
|
|
|
|
q15 |
q16 |
|
|
|
|
|
|
|
|
q16 |
q19 |
|
|
|
|
|
|
|
|
q17 |
|
|
|
|
|
|
|
q18 |
|
q18 |
q19 |
|
|
|
|
|
|
|
|
q19 |
|
|
|
|
|
|
|
|
Как следует из таблицы и из графа, автомат является недетерминированным (находясь в состоянии q0 под действием сигнала х4 он переходит сразу в два состояния).
Получим из недетерминированного автомата детерминированный.
|
q |
x0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
|
q0 |
|
|
q7 |
|
{q1,q3} |
|
q10 |
|
|
{q1,q3} |
|
q2 |
|
|
|
q4 |
|
|
|
q2 |
q5 |
|
|
|
|
|
|
|
|
q4 |
|
q6 |
|
|
|
|
|
|
|
q5 |
|
|
q8 |
|
|
q19 |
|
|
|
q6 |
|
|
q9 |
|
|
q19 |
|
|
|
q7 |
|
|
q9 |
|
|
q19 |
|
|
|
q8 |
|
|
|
q19 |
|
|
|
q0 |
|
q9 |
|
|
|
q19 |
|
|
|
q0 |
|
q10 |
q11 |
|
q17 |
|
|
q14 |
|
|
|
q11 |
|
|
|
q12 |
|
|
|
|
|
q12 |
q13 |
|
|
|
|
|
|
|
|
q13 |
q19 |
|
|
|
|
|
|
|
|
q14 |
|
|
|
q15 |
|
|
|
|
|
q15 |
q16 |
|
|
|
|
|
|
|
|
q16 |
q19 |
|
|
|
|
|
|
|
|
q17 |
|
|
|
|
|
|
|
q18 |
|
q18 |
q19 |
|
|
|
|
|
|
|
|
q19 |
|
|
|
|
|
|
|
|
|
q1q3 |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q2 |
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q4 |
X |
X |
X |
|
|
|
(8,9) |
q5~q6~q7 |
|
|
|
|
|
|
|
|
||
|
q5 |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q6 |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q7 |
X |
X |
X |
X |
|
|
|
|
q8~q9 |
|
|
|
|
|
|
|
|
|
|
q8 |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|
|
|
|
q9 |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
(12,15) |
q11~q14 |
|
|
|
||
|
q10 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
|
|
q11 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
(13,16) |
q12~q15 |
|
||
|
q12 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
|
q13 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
|
|
|
|
q14 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
X |
X |
|
|
q13~q16~q18 |
||
|
q15 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
X |
X |
|
|
|
|
|
q16 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
X |
X |
|
~ |
|
|
q17 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
|
q18 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
X |
X |
|
X |
|
|
q19 |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
X |
|
|
q0 q1q3 q2 |
q4 |
q5 |
q6 |
q7 |
q8 |
q9 |
q10 |
q11 |
q12 |
q13 |
q14 |
q15 |
q16 |
q17 |
q18 |
||
В результате эквивалентными оказались:
q5~q6~q7;
q8~q9;
q11~q14;
q12~q15;
q13~q16~q18.
Введём следующие обозначения:
q0=r0;
q1,q3=r1;
q2=r2;
q4=r3;
q5,q6,q7=r4;
q8,q9=r5;
q10=r6;
q11,q14=r7;
q12,q15=r8;
q13,q16,q18=r9;
q17=r10;
q19=r11;
q20=r12.