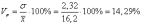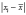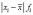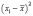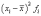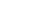Случайные величины. Дискретная случайная величина
Случайной называют величину, которая в результате испытания примет одно и только одно из возможных значений, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Обозначают случайные величины буквами Х, Y,Z,а их возможные значения — х, у,z.
Дискретной называют случайную величину, которая принимает отдельные, изолированные друг от друга значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным, но счетным.
Дискретная случайная величина может быть задана рядом распределения — это соответствие между возможными значениями и их вероятностями:

pi=P(X=xi), i = 1,n.
События X = x1, X = x2,..., X = xnобразуют полную группу, следовательно, сумма вероятностей этих событий равна единице:
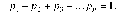
Ряд распределения дискретной случайной величины можно изобразить графически в виде полигона или многоугольника распределения вероятностей. Для этого по горизонтальной оси в выбранном масштабе нужно отложить значения случайной величины, а по вертикальной — вероятности этих значений, тогда точки с координатами (xi,pi) будут изображать полигон распределения вероятностей; соединив же эти точки отрезками прямой, получим многоугольник распределения вероятностей.
Пример 1. Пусть Х — дискретная случайная величина, заданная рядом распределения
Х |
-2 |
-1 |
0 |
2 |
4 |
Р |
0,1 |
0,2 |
0,3 |
0,2 |
0,2 |
Построить полигон и многоугольник распределения вероятностей.
Решение. На оси Х откладываем значения xi, равные -2, -1, 0, 2, 4, а по вертикальной оси вероятности этих значений (рис. 1):
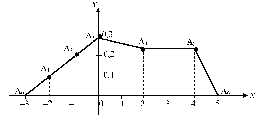
Рис. 1
Точки A1A2, A3, A4, A5изображают полигон распределения, а ломанаяA0A1A2A3A4A5A6— многоугольник распределения вероятностей.
Дискретная случайная величина может быть задана функцией распределения. Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что случайная величина Х примет значение меньшее х:
F(x)=P(X <x)
Функцию F(x) иногда называют интегральной функцией распределения.
Если значения случайной величины — точки на числовой оси, то геометрически функция распределения интерпретируется как вероятность того, что случайная величина Х попадает левее заданной точки х (рис. 2):
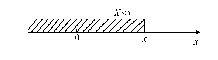 F(x)
F(x)обладает
свойствами:
F(x)
F(x)обладает
свойствами:
1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:
0<F(x)< 1.
Утверждение следует из того, что функция распределения — это вероятность.
2. Функция распределения есть неубывающая функция на всей числовой оси.
3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна 1.
4. Вероятность попадания случайной величины в интервал [x1, x2) (включая x1) равна приращению ее функции распределения на этом интервале, т.е.
P(x1≤X<x2)=F(x2)-F(x1).
Числовые характеристики случайной величины
Математическое ожидание М(Х)дискретной случайной величины
П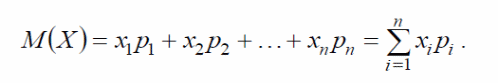 усть
случайная величина Х
может
принимать только значения x1,
x2,...,
xn,
вероятности которых соответственно
равны p1,p2,…,pn.
Тогда математическое ожидание
М(Х)случайной
величины Х
определяется
равенством
усть
случайная величина Х
может
принимать только значения x1,
x2,...,
xn,
вероятности которых соответственно
равны p1,p2,…,pn.
Тогда математическое ожидание
М(Х)случайной
величины Х
определяется
равенством
Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина.
М атематическое
ожидание приближенно равно среднему
арифметическому значений случайной
величины:
атематическое
ожидание приближенно равно среднему
арифметическому значений случайной
величины:
Свойства математического ожидания
1. Математическое ожидание постоянной величины равно самой постоянной
M(C) = C .
2. Постоянный множитель можно выносить за знак математического ожидания
M (CX) = CM (X).
3. Математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий
M(X±Y) = M(X)±M(Y).
4. Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий
M (XY )= M (X) M(Y).
5. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю
M (X - M (X ))= 0.
Дисперсия случайной величины
Только математическое ожидание не может в достаточной степени характеризовать случайную величину.
На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения.
Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата ее отклонения от ее математического ожидания:
D( X) = M[X - M (X )]2.
Дисперсия — это мера рассеяния случайной величины около ее математического ожидания.
Если Х — дискретная случайная величина, то дисперсию вычисляют по следующим формулам:
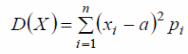
где а = М(Х);
d(x)=m(x2 )-(m(x))2.
Свойства дисперсии случайной величины
1. Дисперсия постоянной величины С равна нулю
d(c)=0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат
d(cx)= C2d(x) .
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин
d(x+y)=D(x)+d(y) .
4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий
d(x-y)=D(x)+d(Y).
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.
Средним квадратическим отклонением случайной величины Х называется арифметическое значение корня квадратного из ее дисперсии
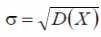 .
.
Среднее квадратическое отклонение характеризует степень отклонения случайной величины от ее математического ожидания и имеет размерность значений случайной величины.
Рассмотрим некоторые распределения дискретной случайной величины.
Биномиальный закон распределения
Если вероятность появления события А в каждом испытании постоянна и равна р,то число появлений события А— дискретная случайная величина Х, принимающая значения 0, 1, 2, …, m, с вероятностями
Pn(m)=Cmpmqn-m(формула Бернулли), где 0<p<1, q= 1 - p,m= 0,1, ...,n.
Математическое ожидание и дисперсия случайной величины Х, распределенной по биномиальному закону, вычисляется по формулам:
M (X ) = np,
D( X )=npq.
Пример 2. В аккредитации участвуют 4 коммерческих вуза. Вероятности пройти аккредитацию и получить сертификат для этих вузов, соответственно равны 0,5; 0,4; 0,3; 0,2. Составить закон распределения числа коммерческих вузов, не прошедших аккредитацию. Найти числовые характеристики этого распределения.
Решение. В качестве случайной величины х выступает число коммерческих вузов, не прошедших аккредитацию. Возможные значения, которые может принять случайная величина х: 0, 1, 2, 3, 4.
Для составления закона распределения необходимо рассчитать соответствующие вероятности.
Обозначим через событие a1— первый вуз прошел аккредитацию, a2— второй, a3— третий, a4— четвертый. Тогда P(A1)= 0,5; P(A2)= 0,4; P(A3)= 0,3; P(A4)= 0,2.
Вероятности
для вузов не пройти аккредитацию
соответственно равны P(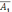 )
)
=1— 0,5=0,5; P( )= 1 — 0,4 = 0,6; p( )= 1 — 0,3 = 0,7; p( )= 1 — 0,2 = 0,8. Тогда имеем:
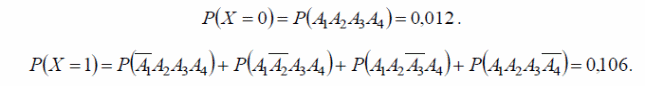

Х |
0 |
1 |
2 |
з |
4 |
Р |
0,012 |
0,106 |
0,320 |
0,394 |
0,168 |
П
Проверка: 0,012 + 0,106 + 0,32 + 0,394 + 0,168 = 1. Вычислим
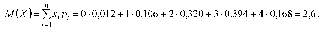
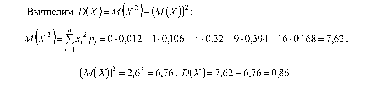
Проверка: 0,012 + 0,106 + 0,32 + 0,394 + 0,168 = 1. Вычислим
Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения числа библиотек, которые последовательно посетит студент, чтобы взять необходимую книгу, если в городе 3 библиотеки.
Решение. В качестве случайной величины Х выступает число библиотек, которые посетит студент, чтобы получить необходимую книгу. Возможные значения, которые примет случайная величина х:1, 2, 3.
Обозначим через событие A1— книга свободна в первой библиотеке,A2— во второй, A3— в третьей. ТогдаP(A1)=Р(A2)=P(A3)= 0,3. Вероятность противоположного события, что книга занята = 1 - 0,3 = 0,7.
Для составления закона распределения рассчитаем соответствующие вероятности:
З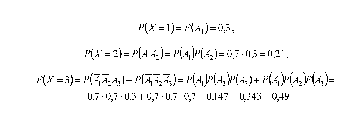 апишем
закон распределения в виде таблицы.
апишем
закон распределения в виде таблицы.
х |
1 |
2 |
3 |
р |
0,3 |
0,21 |
0,49 |
Проверка: 0,3 + 0,21 + 0,49 = 1.
Пример 4.Из поступающих в ремонт 10 часов 7 нуждаются в общей чистке механизма. Часы не рассортированы по виду ремонта. Мастер, желая найти часы, нуждающиеся в чистке, рассматривает их поочередно и, найдя такие часы, прекращает дальнейший просмотр. Составить закон распределения числа просмотренных часов. Найти математическое ожидание и дисперсию этой случайной величины.
Решение. В качестве случайной величины х выступает число просмотренных часов. Возможные значения, которые примет случайная величина х:1, 2, 3, 4. Все значения случайной величины зависимы.
Для составления закона распределения вычислим вероятности того, что случайная величина примет каждое из своих возможных значений. Для расчета вероятностей будем использовать формулу классической вероятности и теорему умножения для зависимых событий.
Пусть событие a1— первые, взятые наугад, часы, нуждающиеся в чистке,
a2— вторые, a3— третьи, a4— четвертые. Тогда имеем:
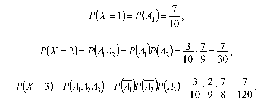
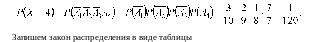
Х |
1 |
2 |
3 |
4 |
Р |
7/10 |
7/30 |
7/120 |
1/120 |
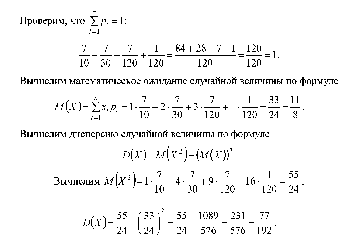
Пример 5.
Имеются данные о пяти промышленных предприятий района.
№ предприятия |
Объем произведенной продукции, тыс. руб. |
Среднесписочное число работающих, тыс. чел |
Выработка на одного работающего, руб. |
1 |
4000 |
4 |
1000 |
2 |
9000 |
6 |
1500 |
3 |
20000 |
10 |
2000 |
4 |
14400 |
8 |
1800 |
5 |
6500 |
5 |
1300 |
Определите для данной совокупности средние показатели: а) объема произведенной продукции; б) числа работающих; в) выработки на одного работающего.
Решение
а)
средний показатель объема произведенной
продукции рассчитаем по форме средней
арифметической невзвешенной.
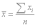 ,
где
xi
– значения объема произведенной
продукции i-го
предприятия, n–
число предприятий.
,
где
xi
– значения объема произведенной
продукции i-го
предприятия, n–
число предприятий.
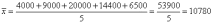 тыс.
руб.
б) средний показатель числа
рабочих рассчитаем по форме средней
арифметической невзвешенной.
тыс.
руб.
б) средний показатель числа
рабочих рассчитаем по форме средней
арифметической невзвешенной.
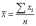 ,
где xi
– среднесписочное число рабочих
i-го
предприятия, n
– число предприятий.
,
где xi
– среднесписочное число рабочих
i-го
предприятия, n
– число предприятий.
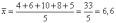 тыс.
чел.
в) средний показатель выработки
на одного работающего рассчитаем по
форме средней гармонической взвешенной.
тыс.
чел.
в) средний показатель выработки
на одного работающего рассчитаем по
форме средней гармонической взвешенной.
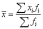 ,
где xi
– выработка на одного работающего i-го
предприятия, fi
– среднесписочное число рабочих i-го
предприятия.
,
где xi
– выработка на одного работающего i-го
предприятия, fi
– среднесписочное число рабочих i-го
предприятия.
 руб.
руб.
Пример 6.
Для изучения качества пряжи была проведена 2%-ая механическая выборка, в результате которой обследовано 100 одинаковых по весу образцов пряжи и получены следующие результаты:
Крепость нити, г |
Число образцов |
До 160 |
2 |
160-180 |
7 |
180-200 |
24 |
200-220 |
40 |
220-240 |
20 |
240-260 |
7 |
и т о г о |
100 |
На основании полученных данных вычислите: 1) среднюю крепость нити; 2) все возможные показатели вариации.
Решение
Среднюю
величину рассчитаем по формуле средней
арифметической взвешенной:
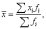 где
xi
- значение осредняемого признака, fi
- частота.
В качестве показателей
вариации рассчитаем:
Среднее линейное
отклонение, определяемое из отношения
суммы, взятых по абсолютной величине
отклонений всех вариант от средней
арифметической, к объему всей
совокупности:
где
xi
- значение осредняемого признака, fi
- частота.
В качестве показателей
вариации рассчитаем:
Среднее линейное
отклонение, определяемое из отношения
суммы, взятых по абсолютной величине
отклонений всех вариант от средней
арифметической, к объему всей
совокупности:
 Дисперсия,
равную среднему квадрату отклонений
индивидуальных значений признака от
их средней величины:
Дисперсия,
равную среднему квадрату отклонений
индивидуальных значений признака от
их средней величины:
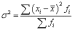 Среднее
квадратическое отклонение, характеризующее
величину, на которую все варианты в
среднем отклоняются от средней
арифметической. Равно корню квадратному
из суммы квадратов отклонений
индивидуальных значений признака отих
средней, т.е. из дисперсии:
Среднее
квадратическое отклонение, характеризующее
величину, на которую все варианты в
среднем отклоняются от средней
арифметической. Равно корню квадратному
из суммы квадратов отклонений
индивидуальных значений признака отих
средней, т.е. из дисперсии:
 Произведем
дополнительные расчеты в таблице для
получения средних величин.
Произведем
дополнительные расчеты в таблице для
получения средних величин.
|
Середина интервала xi |
Частота fi |
xifi |
|
|
|
|
1 |
80 |
2 |
160 |
126,6 |
253,2 |
16027,56 |
32055,12 |
2 |
170 |
7 |
1190 |
36,6 |
256,2 |
1339,56 |
9376,92 |
3 |
190 |
24 |
4560 |
16,6 |
398,4 |
275,56 |
6613,44 |
4 |
210 |
40 |
8400 |
3,4 |
136 |
11,56 |
462,4 |
5 |
230 |
20 |
4600 |
23,4 |
468 |
547,56 |
10951,2 |
6 |
250 |
7 |
1750 |
43,4 |
303,8 |
1883,56 |
13184,92 |
|
1130 |
100 |
20660 |
250 |
1815,6 |
20085,36 |
72644 |
В
результате получим следующие
значения:
Средняя крепость нити
 г.
г.
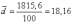 г.
г.
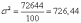
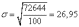 г.
Вычислим
относительные показатели вариации.
Коэффициент
осцилляции:
г.
Вычислим
относительные показатели вариации.
Коэффициент
осцилляции: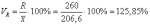 Линейный
коэффициент вариации:
Линейный
коэффициент вариации: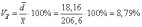 Коэффициент
вариации:
Коэффициент
вариации: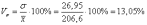 Коэффициент
вариации меньше 33%, значит данная
совокупность однородна, колеблемость
признака возле среднего значения
небольшая.
Коэффициент
вариации меньше 33%, значит данная
совокупность однородна, колеблемость
признака возле среднего значения
небольшая.
Пример 7.
Для контроля за качеством поступившей партии товара произведено 5%-ное выборочное обследование. При отборе в выборку образцов по схеме механического отбора получены следующие данные о содержании влаги:
Влажность, % |
Количество образцов |
До 14 |
20 |
14-16 |
30 |
16-18 |
25 |
18-20 |
20 |
20 и выше |
5 |
Итого |
100 |
Определите:
1.
Средний процент товара влажности.
2.
Показатели вариации (абсолютные и
относительные).
Решение
Средняя
арифметическая взвешенная вычисляется
по формуле:
где
xi
- значение влажности,
fi
- количество образцов.
Среднее линейное
отклонение определяется из отношения
суммы, взятых по абсолютной величине
отклонений всех вариант от средней
арифметической, к объему всей
совокупности:
Дисперсией
называется средний квадрат отклонений
индивидуальных значений признака от
их средней величины:
Среднее
квадратическое отклонение - это показатель
вариации, характеризующий величину, на
которую все варианты в среднем отклоняются
от средней арифметической. Равно корню
квадратному из суммы квадратов отклонений
индивидуальных значений признака отих
средней, т.е. из дисперсии:
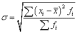 Произведем
дополнительные расчеты в таблице для
получения средних величин.
Произведем
дополнительные расчеты в таблице для
получения средних величин.
|
xi |
fi |
xifi |
|
|
|
|
1 |
13 |
20 |
260 |
3,2 |
64 |
10,24 |
204,8 |
2 |
15 |
30 |
450 |
1,2 |
36 |
1,44 |
43,2 |
3 |
17 |
25 |
425 |
0,8 |
20 |
0,64 |
16 |
4 |
19 |
20 |
380 |
2,8 |
56 |
7,84 |
156,8 |
5 |
21 |
5 |
105 |
4,8 |
24 |
23,04 |
115,2 |
|
85 |
100 |
1620 |
12,8 |
200 |
43,2 |
536 |
В
результате получим следующие
значения:

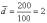
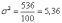
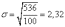 Вычислим
относительные показатели вариации.
Коэффициент
осцилляции:
Вычислим
относительные показатели вариации.
Коэффициент
осцилляции: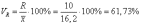 Линейный
коэффициент вариации:
Линейный
коэффициент вариации: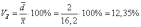 Коэффициент
вариации:
Коэффициент
вариации: