2. Produkční a nákladová funkce V dlouhém období

= všechny vstupy variabilní

= můžeme je mezi sebou nahrazovat (substituovat)

Produkční funkce v dlouhém období (LR)

• představuje maximální objem produkce, který je možno vyrobit s různými kombinacemi výrobních faktorů při dané technologii

• druhou důležitou vlastností zde jsou výnosy z rozsahu

• Q = f (K,L) » práce a kapitál;

• neplatí zákon klesajících výnosů;

• Q = f(K,L)

• K » kapitál

• L » práce (labour)

Izokvanta a její vlastností

• takové kombinace vstupů, kterými vyrobíme stejný objem produkce

• výstup roste směrem od počátku, tj. jednotlivé izokvanty se nemohou protínat

• konvexní a klesajicí

• nekonečné množství

• směrem od počátku výstup roste

• mapa izokvant je zobrazení dlouhodobé

• vidíme jí jenom ze předu

• produkční funkce (je to vlastně indiferentní křivka firmy)

• každé izokvantě můžeme přiřadit konkrétní číslo (hodnotu)

Grafickým znázorněním dlouhodobé produkční funkce je izokvantová mapa

Sklon izokvanty

• směrnice izokvanty = mezní míra technické substituce (MRTS ~ marginal rate of technical substitution) = technické nahrazení dvou vstupů

• je to záporná směrnice, ale uvažujeme v absolutní hodnotě

_{MRTS =} ∆K ₌ MPP_L

∆L MPP_K

Q = TPP_L + TPP_K

∆Q = 0 = Q

MPP_{K =} ∆TPP

∆K

• nahrazujeme kapitál prací

• práce je produktivní, musí vybavit stroje, které jsou jako takové neproduktivní

• ∆Q = 0 » na izokvantě; mění se produktivita (čím méně kapitálu, tím jeho produktivita poroste)

• ∆K * MPP_K = ∆L * MPP_L

• pohybem po izokvantěmezní produktivita kapitálu roste, mezní produktivita práce klesá

• výnosy z rozsahu se projevují zhušťováním a vzdalováním izokvant

Vlastnosti dlouhodobé produkční fce

• substituce vstupů – substituje K prací (L)

• výnosy z rozsahu

Nákladová funkce v dlouhém období

Izokosta

• kombinace výrobních faktoru v rámci stejných celkových nákladů (max.dostupné kombinace vstupů vzhledem k prostředkům, které má firma k dispozici a vzhledem k cenám vstupů)

• obdoba linie příjmů

• TC je linie celkových nákladů

• TC = (Pl * L) + (Pk * K);

Pl*L = náklady na práci

Pk*K = náklady na kapitál

• ∆K/∆L = Pl/Pk

• směrnice izokosty: K= (TC/Pk) – ((Pl*L)/Pk) – záporná směrnice, ale uvažujeme v absolutní hodnotě

Nákladové optimum = místo dotyku izokvanty a izokosty. Řeší za problém :

• konkrétní objem produkce s min. náklady - ideální kombinace vstupů vzhledem k nejnižším nákladům

• dané náklady – jak vyrobit toho co nejvíc

• Bod E (nákladové optimum) = průnik izokvanty a izokosty;

• Směrnice jsou s mínusem, tj. jsou klesajicí

• Pl/Pk = MPPl / MPPk;

• MRTS = ∆K/∆L = MPl/MPk = Pl / Pk » platí pro optimální kombinaci vstupů;

• MPPk/Pk = MPPl / Pl » pravidlo nejnižších (stejných) nákladů; u všech spotřebovaných vstupů musí dojít k vyrovnání mezních produktů a cen (hledáme ideální kombinaci); neplatí v E;

GRAF!!!!!!!!!!!!!!

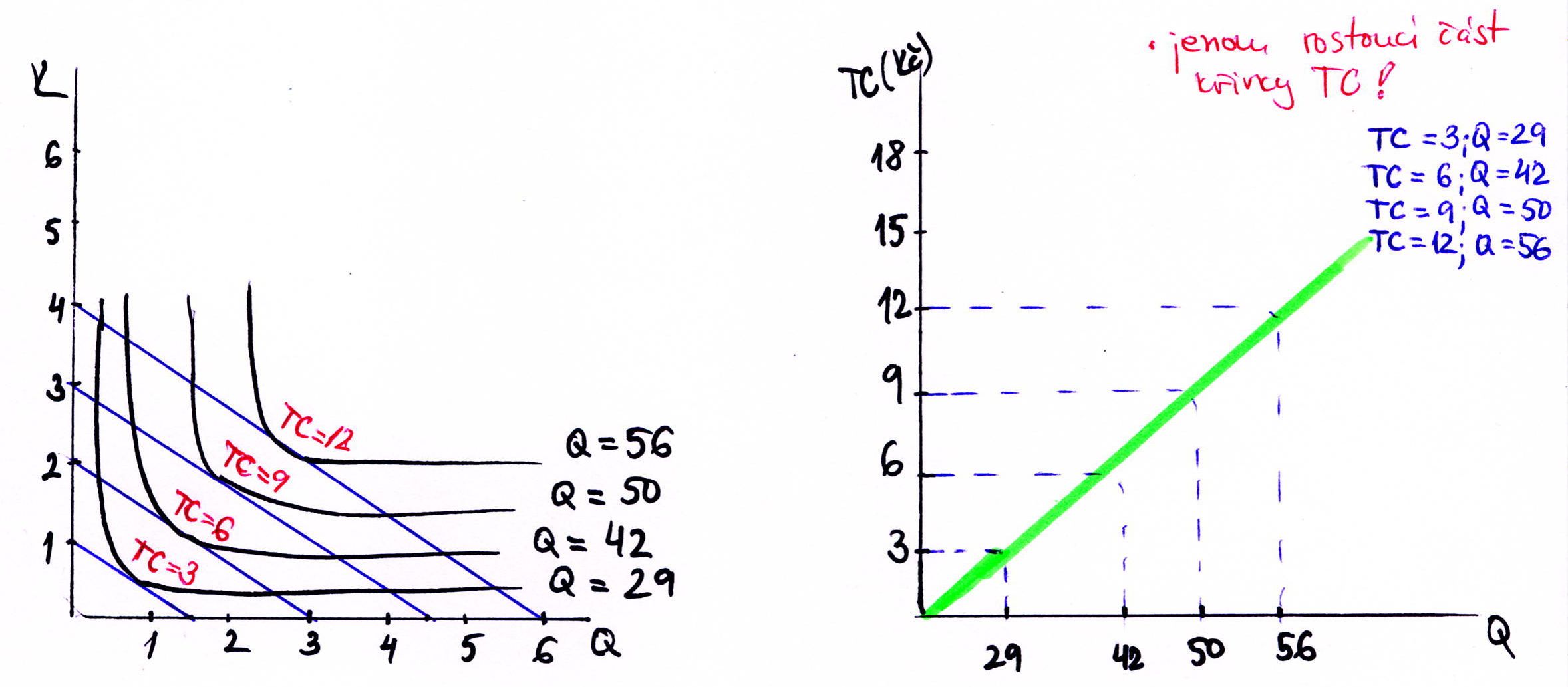
Křivka dlouhodobých nákladů TC (Pk=3, Pl=2)

......z jednotlivých nákladových optim složíme křivku dlouhodobých nákladů (její rostoucí část)

. .....jak vypadá křivka TC.......» záleží na výnosech z rozsahu:

1. náklady rostou pomalu – rostoucí výnosy z rozsahu;

2. náklady rostou rychle – klesající výnosy z rozsahu;

Dlouhodobé náklady odvodíme jako množinu nákladových optim

Jednotkové náklady

3. Příjmy

TR (total revenue) celkové příjmy neboli tržby, obrat

• celkové prostředky, které firma získá za prodej svých výrobků

• jednotkou jsou Kč

TR = Q*P

AR (average revenue) průměrné příjmy

= jaké množství peněž nám přinese jedna prodaná jednotka zboží, tj. jsou rovni ceně jednoho vyrobku!!! A to platí vždy !!!

• jednotkou je Kč/Q

• zachycuje vztah mezi množstvím a cenou a to je na úrovni individuální poptávky po výrobku jedné firmy

_{AR =} TR _{= P}

_Q

MR (marginal revenue;) mezní příjmy

= dodatečné množství peněz, které firma získá prodejem dodatečné jednotky zboží

• jednotkou je Kč/Q

• přírůstková veličina

• jak se změní TR, když prodáme ještě jeden výrobek

_{MR =} ∆TR

∆Q

Tvar křivek příjmů závisí na typu tržní struktury (protože závisí na ceně), respektive typu konkurence (dokonalá/nedokonalá)

X

Nákladová křivky jsou shodné v dokonalé a nedokonalé konkurenci (závisí na produkční funkci a na výnosech z variabilního vstupu v krátkém období a na výnosech z rozsahu v dlouhém období).

4. Zisk

• značí se písmenem π (pí)

• π = TR – TC → obecná zisková funkce (celkový zisk)

• zisk na jednotku produkce = průměrný zisk π ₌ TR _- TC → Øπ = AR – AC

Q Q Q

• 2 pohledy na zisk

  • účetní zisk = TR – explicitní náklady (je to zisk z pohledu podnikatele, veden v ÚČE)

  • ekonomický zisk = TR – TC (explicitní + implicitní)

    • EZ = ekonomický zisk (někde se používá i zkratka ČEZ = čistý ekonomický zisk)

    • EZ = účetní zisk – implicitní náklady

    • EZ může nabývat tří hodnot:

1. EZ > 0

2. EZ < 0

3. EZ = 0

• normální zisk - je kvantitativně roven implicitním (alternativním) nákladům

  • EZ = 0; TR = TC (nejsou zachyceni implicitní náklady); MR = AC ( vyjádřeno v jednotkových veličinách)

  • Např.. implicitních nákladů – podnikatel se rozhoduje, zda bude šít boty (je švec), něco dá na materiál, něco vydělá.. kladný zisk vyjde 5000 Kč. Nechá-li se zaměstnat – dostane mzdu 15 000 Kč.