Правило округления чисел

Округлить число – значит заменить его числом с меньшим числом значащих цифр.

Абсолютная величина разности называется погрешностью округления.

Число выбирается так, чтобы погрешность округления была наименьшей.

Если первая слева отбрасываемая цифра меньше 5, то округляют с недостатком, а если эта цифра 5 или больше 5, то округляют с избытком.

Например, 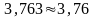(до сотых), (до десятых).

Погрешности вычислений с приближенными данными

Правило 1. При сложении и вычитании границы абсолютных погрешностей исходных данных складываются:

,

Правило 2. При умножении и делении границы относительных погрешностей исходных данных складываются:

,

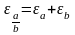
Правило 3. При возведении в степень граница относительной погрешности основания степени умножается на показатель степени:

Пример. Найти сумму чисел:

Все ли цифры в полученной сумме верны? Оценим границу абсолютной погрешности по формуле .

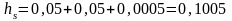
При такой границе абсолютной погрешности ( ) в приближенном значении суммы являются верными лишь две цифры (в разрядах десятков и единиц):

Пример. Найти произведение двух приближенных чисел и .

Все ли цифры произведения верны? Чтобы ответить на этот вопрос, надо оценить границу абсолютной погрешности результата.. она находится так. Сначала вычислим относительные погрешности множителей.

Из записи приближенного числа находим и 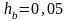(в строгом смысле), тогда , . По формуле находим .

Используя формулу , находим

Такая граница абсолютной погрешности означает, что в результате только одна верная цифра

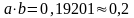
Пример. Вычислить . Найти относительную погрешность вычисления.

Найдем относительную погрешность по формуле :

.

Ответ: 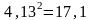с относительной погрешностью до 0,3%.

Вычисления без строго учета погрешностей выполняют по правилам, позволяющим быстро без громоздких вычислений получить результат нужной точности. Они называются правилами подсчета цифр.

Правило1. При сложении и вычитании десятичных дробей в результате сохраняют столько десятичных знаков, сколько их в числе с наименьшим числом десятичных знаков.

При сложении и вычитании целых чисел их записывают в стандартном виде и вынося за скобки наибольшую степень десяти.

Правило 2. При умножении и делении приближенных чисел в результате сохраняют столько значащих цифр, сколько их в числе с наименьшим числом значащих цифр.

Правило 3. При возведении в квадрат и куб в результате сохраняют столько значащих цифр, сколько их в основании степени.

Правило 4. При извлечении квадратного или кубического корня в результате сохраняют столько значащих цифр, сколько их в подкоренном выражении.

Правило 5. В промежуточных вычислениях сохраняют на одну цифру больше, чем это рекомендуется предыдущими правилами. В окончательном результате эта запасная цифра округляется.

Пример. Вычислим .

Сделаем грубую оценку результата: .

Вычислим

Оценим границу абсолютной погрешности :

При таком в результате последняя верная цифра в разряде десятых. Следовательно, в результате две верные цифры, поэтому в исходных данных оставляем три значащих цифры:

Пример. С какой точностью должны быть измерены масса стального шара и его диаметр, чтобы вычислить плотность материала с точностью до 0,1%. Масса шара кг, диаметр 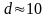см.

1. плотность определяется по формуле , , 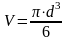тогда .

2. 6 – число точное, – можно взять с большой точностью.

Найдем относительную погрешность . Измерить массу с большой точностью легче, чем измерить длину, поэтому будем считать, что составляет одну сотую . Остальную часть отнесем на . Это значит, что относительная погрешность и должны быть следующими:

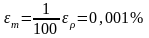
или

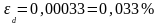
3. Находим границы абсолютной погрешности и :

(кг) (г) (мг)

(см) (мм)

Следовательно, чтобы вычислить с точностью до 0,1%, нужно массу взвесить с точностью до десятков миллиграмм, а диаметр с точностью до сотых долей миллиметра.

При выполнении вычислений важно расположить удобно записи, так, чтобы содействовать быстрому и безошибочному ходу вычислений. Для этого производится расписка формулы.

Рассматриваем данную формулу и устанавливаем, в какой последовательности и какие действия нужно производить. В точном соответствии с порядком действий составляем таблицу. В которой каждый столбец предназначен для записи результата определенной операции.

Так, если требуется вычислить значения функции 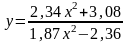, то порядок вычислений должен быть таким:

1. возвести в квадрат

2. умножить результат операции 1 на 2,34

3. сложить результат операции 2 с числом3,08

4. умножить результат операции 1 на 1,87

5. вычесть из результата операции 4 число 2,36

6. разделить результат операции 3 на результат операции 5.

Это и будет окончательный результат всего вычисления. Производя «расписку формулы», составим таблицу такого вида:

		(II)	(III)+3,08	(II)	(V)-2,36	(IV): (VI)
I	II	III	IV	V	VI	VII

Таблицу начертить на отдельном листе бумаги (расчетном бланке) и выполняя последовательно вычисления. Записывать немедленно каждый полученный результат в соответствующий столбец таблицы.

Все результаты вычислений должны контролироваться, т.к. в процессе вычислений могут возникать просчеты.

При вычислении значений некоторой величины, заданной формулой поступают так:

1. определяем, с какой точностью следует исходные данные, чтобы получить результат с заданной точностью;

2. определяем точность результата промежуточных действий;

3. составляем расчетную таблицу;

4. проводим вычисления, пользуясь расчетной таблицей;

5. округляем найденные значения;

6. проводим контроль вычислений.

При выполнении пунктов 1 и 2 обычно на практике применяют правило запасной цифры, т.е. во всех исходных данных и в промежуточных результатах берут на одну верную цифру больше, чем это требуется в окончательном результате.