Задание на 06.10.2012 (суббота) Тема: Приближенные вычисления и вычислительные средства

Выполнить на двойных листах

Сделать конспект, записав определения:

1. Абсолютной погрешности приближенного числа.

2. Границы абсолютной погрешности.

3. Относительной погрешности.

4. Верной и значащей цифры приближенного числа.

На практике при решении задач часто приходится иметь дело с приближенными значениями величин. К ним относятся: результаты измерения различных величин (расстояния, массы, объема и т.д.); результаты подсчета большого количества предметов; измерения, полученных значений на графиках, диаграммах, номограммах, проектные данные и т.д.

Абсолютной погрешностью приближенного значения числа называется модуль разности между точным числом и его приближенным значением 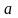и обозначается :

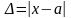
Пример 1. Пусть даны следующие приближения значения числа : ; ; .

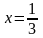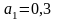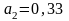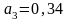Найдем абсолютные погрешности этих приближенных значений числа по формуле и определим, какое из этих трех приближений лучше:

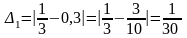
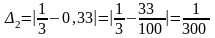
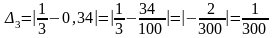
Сравнение абсолютных погрешностей показывает, что лучшим приближением числа 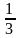является .

На практике часто точное значение числа бывает не известно, поэтому найти абсолютную погрешность нельзя. Однако, если известны приближения с избытком и недостатком, то можно дать оценку абсолютной погрешности.

Оценить абсолютную погрешность, т.е. указать число, которое не может превысить абсолютную погрешность.

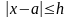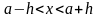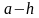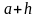Если , то , где – приближенное значение числа по недостатку; – приближенное значение числа по избытку. Можно записать и так 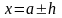. Положительное число 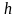называют границей абсолютной погрешности.

Например, если 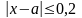, то число 0,2 является границей абсолютной погрешности числа . Но и любое число, большее, чем 0,2, также является границей абсолютной погрешности. На практике стараются выбрать возможно меньшее и простое по записи число , удовлетворяющее неравенству .

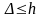Знание только абсолютной погрешности недостаточно для характеристики качества измерения или вычисления. Качество измерения или вычисления характеризуется относительной погрешностью.

Пример. Измерим толщину книги , высоту стола и длину классной доски линейкой с сантиметровой шкалой. С помощью такой линейки можно получить результаты с точностью до 0,5 см.

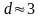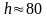Пусть результаты измерения: см, см, 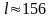см. По условию 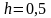см. Какое измерение точнее?

Относительной погрешностью приближенного значения называется отношение границы абсолютной погрешности к модулю числа :

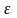( – эпсилон)

Вычислим относительную погрешность проведенных измерений , и .

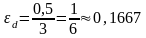
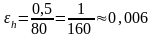
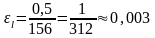
Обычно относительную погрешность выражают в процентах:

, , .

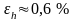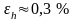Чем меньше относительная погрешность, тем выше качество измерения или вычисления.

В данном примере самое высокое качество измерения длины классной доски.

Десятичная запись приближенных чисел

Приближенные числа удобно записывать в виде конечных десятичных дробей. При этом устанавливается такой способ записи приближенного числа, чтобы по записи числа в виде десятичной дроби можно было видеть его абсолютную погрешность.

Цифра 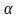называется верной, если абсолютная погрешность не превосходит половины единицы того разряда, к которому принадлежит цифра .

Например. Пусть даны приближенные числа ; ; 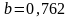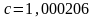. Из записи чисел видно, что , , .

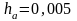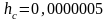Замечание 1. В записи приближенных чисел сохранять только верные цифры.

Замечание 2. Если приближенное число записано с некоторым числом десятичных знаков, причем последние десятичные знаки суть нули, являются верными цифрами, то их не следует отбрасывать.

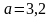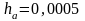Например, если и , то следует писать .

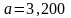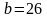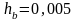Если и , то следует писать .

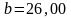Замечание 3. если в целом числе последние цифры сомнительные, то их исключают из записи числа.

Например, если 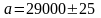, то правильная запись числа .

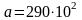Замечание 4. В записи приближенного числа последняя цифра десятичной записи указывает на точность приближения, т.е. граница абсолютной погрешности не превосходит единицы последнего разряда.

Например, если 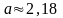, то , т.е. .

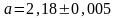Все верные цифры в записи приближенного числа, кроме нулей, стоящих левее первой, отличной от нуля цифры, называются значащими.

Например, в числе 2,17 – три значащие цифры; в числе 0,0028 – две; в числе 0б606 – три; в числе 2,600 – четыре, а в числе 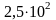– две значащие цифры.