
- •Скалярное произведение векторов
- •2. Векторное произведение векторов
- •3. Смешанное произведение векторов
- •Аналитическая геометрия
- •1. Прямоугольная система координат
- •Полярная система координат
- •Прямая на плоскости Различные виды уравнения прямой
- •У равнение прямой с угловым коэффициентом:
- •О бщее уравнение прямой:
- •Уравнение прямой, проходящей через данную точку в
- •Уравнение прямой, проходящей через две данные точки
- •Нормальное уравнение прямой:
- •У равнение прямой в полярных координатах:
- •Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых, пересечение прямых
- •Расстояние от данной точки до данной прямой
- •Плоскость в пространстве Различные виды уравнения плоскости
- •У равнение плоскости, проходящей через
- •О бщее уравнение плоскости:
- •Нормальное уравнение плоскости:
- •Расстояние от данной точки до данной прямой
- •П рямая в пространстве Различные виды уравнения прямой в пространстве
- •К анонические уравнения прямой,
- •Параметрические уравнения прямой, проходящей через
- •Уравнения прямой, проходящей через две точки
- •Угол между двумя прямыми, условия параллельности и перпендикулярности прямых
- •Прямая и плоскость в пространстве
- •Кривые второго порядка
- •Окружность
СПРАВОЧНЫЕ МАТЕРИАЛЫ
ВЕКТОРНАЯ АЛГЕБРА
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
ВЕКТОРНАЯ АЛГЕБРА
ВЕКТОРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ. РАЗЛОЖЕНИЕ ВЕКТОРОВ
Вектор
– направленный отрезок. Вектор с началом
в точке А
и концом в точке В
обозначается
символом
![]() (или одной буквой:
(или одной буквой:
![]() ,
,
![]() ,
… , или: a,
b,
… ). Длина отрезка АВ
называется длиной
(модулем)
вектора
и обозначается |
|, |
|,
|a|.
,
… , или: a,
b,
… ). Длина отрезка АВ
называется длиной
(модулем)
вектора
и обозначается |
|, |
|,
|a|.
Вектор, длина которого равна нулю, называется нулевым
вектором
и обозначается
![]() (0).
(0).
Вектор, длина которого равна единице, называется единичным
вектором
и обозначается через
![]() (е).
(е).
Единичный вектор, направление которого совпадает с
направлением
вектора
,
называется ортом
вектора
и обозначается
![]() .
.
Два вектора, имеющие одинаковую длину и противоположные
направления,
называются противоположными.
Вектор, противоположный вектору
![]() ,
обозначается –
.
,
обозначается –
.
Векторы и называются коллинеарными, если они лежат на
одной прямой или на параллельных прямых. Записывают: || .
Три (и более) вектора называются компланарными, если они
лежат в одной плоскости или в параллельных плоскостях.
Два коллинеарных вектора и называются равными ( = ),
если они одинаково направлены и имеют равные длины.
Суммой
двух векторов
и
называется вектор
![]() ,
соединяющий
,
соединяющий
начало вектора с концом вектора , отложенного от конца вектора . Обозначение: = + .
Геометрически сумма векторов получается с помощью правил
«треугольника» (рис.1а) или «параллелограмма» (рис.1.б):
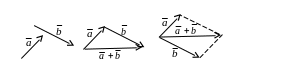
а) б)
Рис.1.
Под разностью векторов и понимается вектор такой, что
+ = .
Обозначение: = – .
Справедливо равенство: – = + (– ).
Произведением
вектора
≠
![]() на число
на число
λ ≠ 0 называется вектор, имеющий длину | λ | ∙ | | и направление,
совпадающее с направлением вектора , если λ > 0; противоположное ему, если λ < 0.
Обозначение: λ ∙ .
Каждый вектор равен произведению его модуля на его орт:
= | | ∙ .
Признак коллинеарности векторов: два ненулевых вектора
и коллинеарны тогда и только тогда, когда один из них есть произведение другого на некоторое число: = λ .
Признак компланарности векторов: три ненулевых вектора , , компланарны тогда и только тогда, когда один из них является линейной комбинацией других, т.е. = λ1 + λ2 (λ1 и λ2 – одновременно не равные нулю числа).
Пример 1. В треугольнике АВС
дано:
![]() =
=
![]() ,
,
![]() =
=
![]() .
.



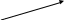

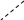
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 Точка М – середина стороны ВС.
Выразить вектор
Точка М – середина стороны ВС.
Выразить вектор
![]()
через векторы и .
• Через точку М проведем прямые, параллельные сторонам
АВ и АС. Получим параллелограмм АВ1МС1 (см. рис.).
Следовательно,
=
![]() +
+![]() .
Т.к. В1М
и
С1М
– средние
.
Т.к. В1М
и
С1М
– средние
л





![]() инии,
то АВ1
= В1В,
АС1
= С1С
и т.о.,
=
инии,
то АВ1
= В1В,
АС1
= С1С
и т.о.,
=
![]() +
=
(
+
).
+
=
(
+
).
Пример 2. В параллелограмме АВСD
дано:
=
,
![]() =
.
=
.
Выразить диагонали (векторы)
и
![]() через
и
.
через
и
.
• См. рис.
=
+
,
![]() =
–
.
=
–
.
Пример 3. Даны векторы
и
.
Коллинеарны ли векторы
![]() =
– 2
=
– 2![]() и
и
![]() = –
+ 6
?
= –
+ 6
?
• = – – выполняется условие коллинеарности векторов => векторы и коллинеарны.

![]()
![]() Проекцией
вектора
Проекцией
вектора
![]() на о
на о![]() сь
l
называется
сь
l
называется
ч исло,
равное д
исло,
равное д
![]()
![]() лине
вектора
лине
вектора
![]() ,
взятой со
,
взятой со
з![]() наком
«плюс», если направление вектора
наком
«плюс», если направление вектора
совпадает с направлением оси и со знаком Рис.2.
«минус» в противном
случае. Точки
![]() и
и
![]() –
–
проекции точек А и В на ось l (рис.2).
Обозначение:
![]() или
или
![]() .
.
Основные свойства проекции:
1.
![]() (
+
)
=
+
;
(
+
)
=
+
;
2. (λ ) = λ ∙ ;
Если
![]() ,
,
![]() ,
,
![]() – орты координатных осей прямоугольной
системы координат Oxyz,
то любой вектор
единственным образом можно представить
в виде их суммы (линейной комбинации) с
коэффициентами ах,
ау,
аz:
– орты координатных осей прямоугольной
системы координат Oxyz,
то любой вектор
единственным образом можно представить
в виде их суммы (линейной комбинации) с
коэффициентами ах,
ау,
аz:
= ах ∙ + аy ∙ + аz ∙ .
Коэффициенты ах, ау и аz линейной комбинации называются координатами вектора в базисе , , .
Обозначение: = { ах, ау, аz } или = ах ∙ + аy ∙ + аz ∙ .
Координаты вектора
в базисе
,
,
,
= { ах,
ау,
аz
}, совпадают с координатами точки М
– конца вектора
=
![]() в прямоугольной системе координат
Oxyz:
М (ах,
ау,
аz).
в прямоугольной системе координат
Oxyz:
М (ах,
ау,
аz).
Длина
вектора
определяется по формуле |
|
=![]() .
.
Вектор образует с координатными осями Ox, Oy и Oz углы α, β и γ соответственно.
Направление вектора определяется с помощью направляющих косинусов: cos α, cos β, cos γ, вычисляемых по формулам:
cos
α
=
![]() ,
cos
β
=
,
cos
β
=
![]() ,
cos
γ
=
,
cos
γ
=
![]() .
.
Направляющие косинусы связаны соотношением
cos2α + cos2 β + cos2 γ = 1.
Координаты
орта вектора
– это его направляющие косинусы:
=
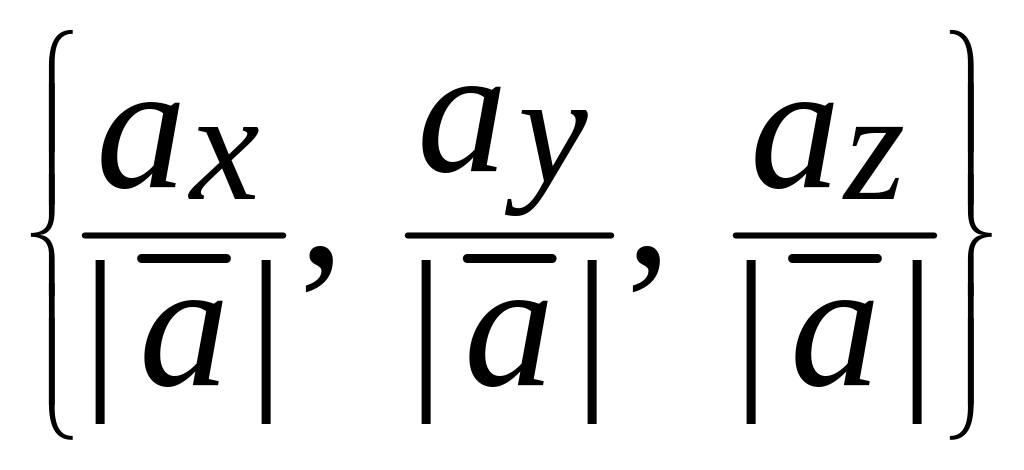 .
.
Пусть векторы
![]() и
и
![]() заданы своими координатами:
заданы своими координатами:
= { ах, ау, аz } и = { bх, bу, bz }.
Векторы
и
равны тогда и только тогда, когда равны
их соответствующие координаты,
т.е.
=
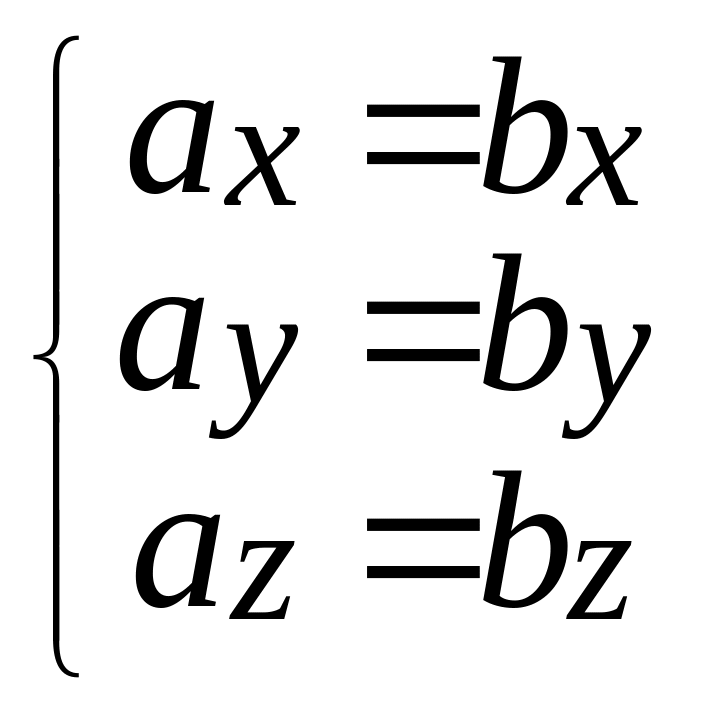 .
.
Векторы и коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.
||
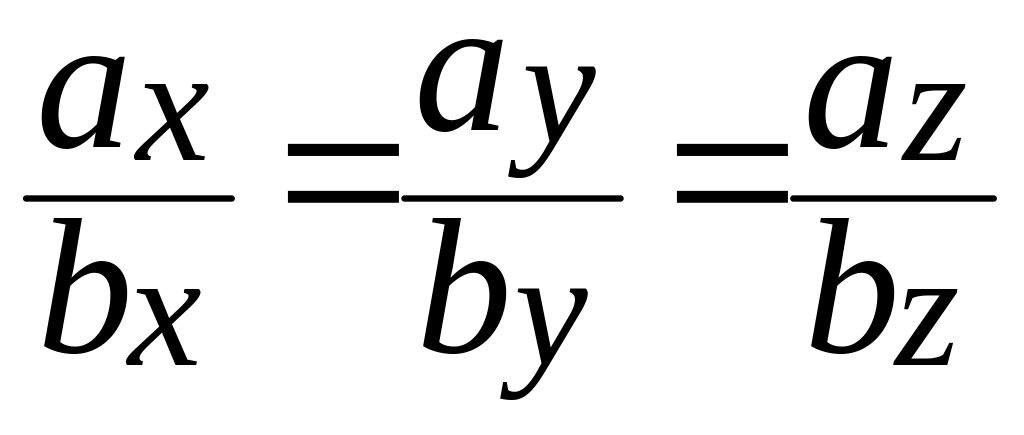 .
.
При сложении векторов их одноименные координаты складываются, при вычитании – вычитаются, при умножении вектора на число – умножаются на это число:
![]() =
{
ах
bх,
аy
by,
аz
bz
},
=
{
ах
bх,
аy
by,
аz
bz
},
λ = { λ ах, λ ау, λ аz }.
Вектор
![]() =
,
соединяющий начало координат с
произвольной точкой
М (x,
y,
z)
пространства
называется
радиус-вектором
точки
М.
Координаты
точки – это координаты ее радиус-вектора
= { x,
y,
z
} или
= x
∙
+ y
∙
=
,
соединяющий начало координат с
произвольной точкой
М (x,
y,
z)
пространства
называется
радиус-вектором
точки
М.
Координаты
точки – это координаты ее радиус-вектора
= { x,
y,
z
} или
= x
∙
+ y
∙
![]() + z
∙
.
+ z
∙
.
Если вектор
![]() =
=
![]() задан точками А(x1,
y1,
z1)
и В(x2,
y2,
z2),
то его координаты ах,
ау,
аz
вычисляются
по формулам
задан точками А(x1,
y1,
z1)
и В(x2,
y2,
z2),
то его координаты ах,
ау,
аz
вычисляются
по формулам
ах = x2 – x1, ay = y2 – y1, aх = z2 – z1:
= = { x2 – x1, y2 – y1, z2 – z1}.
Пример 4. Даны точки А (3; –4; 1) и В (4; 6; –3). Найти координаты вектора = .
• Из координат конечной точки вычитаем координаты начальной точки. Имеем:
ах = 4 – 3 = 1, ay = 6 – (–4) = 10, аz = –3 – 1 = –4. Т.о., = = {1; 10; –4}.
Пример 5. Даны три последовательные вершины параллелограмма: А (1; –2; 3),
В (3; 2; 1), С (6; 4; 4). Найти координаты его четвертой вершины D.
• Обозначим координаты вершины D
через х, у и z,
т.е. D (х;
у; z).
Имеем:
![]() =
=![]() .
Находим координаты векторов
и
:
.
Находим координаты векторов
и
:
= {6 – 3; 4 – 2; 4 – 1} = {3; 2; 3}, = {x – 1; y + 2; z – 3}.
Из равенства векторов и следует: x – 1 = 3, y + 2 = 2, z – 3 = 3. Отсюда:
x = 4, y = 0, z = 6. Т.о., D (4; 0; 6).
Пример 6. Найти координаты вектора , если известно, что он направлен в
противоположную сторону к вектору
=
5![]() –
4
–
4![]() +
2
+
2![]()
![]() ,
и его модуль равен 5.
,
и его модуль равен 5.
• Можно записать, что
= 5![]() .
Т.к. вектор
направлен в противоположную сторону
к вектору
,
то
=
–
.
Т.к. вектор
направлен в противоположную сторону
к вектору
,
то
=
–![]() .
Найдем орт
.
Из равенства
=
|
|
находим
=
.
Найдем орт
.
Из равенства
=
|
|
находим
=
![]() .
Но
|
|
=
.
Но
|
|
=![]() = 7. Значит,
=
= 7. Значит,
=
![]() –
–
![]() +
+
![]() .
Следовательно,
=
–
+
–
и
= 5
=
–
.
Следовательно,
=
–
+
–
и
= 5
=
–![]() +
+
![]() –
–
![]() .
.
Пример 7. Вектор составляет с осями Ох и Оу углы α = 60° и β = 120°. Найти
его координаты, если | | = 2.
• Пусть х, у, z –
координаты вектора
,
т.е.
= {x; y;
z}. Координаты
вектора
найдем из соотношений cosα
=![]() ,
cosβ =
,
cosβ =![]() ,
cosγ =
,
cosγ =![]() .
Предварительно найдем cosγ
из соотношения cos2α
+ cos2β
+ cos2γ
= 1: cos2γ
= 1 – cos2α
– cos2β
=
.
Предварительно найдем cosγ
из соотношения cos2α
+ cos2β
+ cos2γ
= 1: cos2γ
= 1 – cos2α
– cos2β
=
= 1 –
![]() –
–
![]() =
=
![]() => cosγ =
=> cosγ = ![]() .
Условию задачи удовлетворяют два
вектора:
.
Условию задачи удовлетворяют два
вектора:
![]() с направляющими косинусами cosα
=
,
cosβ = –
,
cosγ =
и
с направляющими косинусами cosα
=
,
cosβ = –
,
cosγ =
и
![]() с направляющими косинусами cosα
=
,
cosβ = –
,
cosγ = –
.
с направляющими косинусами cosα
=
,
cosβ = –
,
cosγ = –
.
Т.к. направляющие косинусы – это координаты орта вектора , то
= |
|
= {2
;
2 ![]() ;
2
}
= {1; –1;
},
;
2
}
= {1; –1;
},
= |
|
![]() = {2
;
2
;
2
= {2
;
2
;
2 ![]() }
= {1; –1; –
}
}
= {1; –1; –
}
Пример 8. При каких значениях α и β векторы = –2 + 3 + α и
= β – 6 + 2 коллинеарны?
• Т.к.
||
,
то их координаты должны быть
пропорциональными, т.е. должны
выполняться равенства
![]() =
=
![]() =
=
![]() .
Отсюда находим, что α = –1, β = 4.
.
Отсюда находим, что α = –1, β = 4.
Пример 9. Разложить вектор = {9; 4} по векторам = {1; 2} и = {2; –3}.
• Требуется представить вектор
в виде линейной комбинации векторов.
и
,
т.е. в виде
= λ
+
,
где λ и
– числа. Используя определение
равенства векторов, получим {9; 4} =
λ{1; 2} + {2; –3}
или
![]() .
Решая данную систему уравнений
относительно λ и
, получим λ = 5,
= 2. Следовательно,
= 5
+ 2
.
.
Решая данную систему уравнений
относительно λ и
, получим λ = 5,
= 2. Следовательно,
= 5
+ 2
.
Пример 10. Дана сила
![]() = {4; 4; –4
}.
Найти величину и направление
.
= {4; 4; –4
}.
Найти величину и направление
.
• Величина силы: |
|
=![]() =
8.
=
8.
Направляющие косинусы вектора :
cosα =![]() =
=![]() =
,
cosβ =
=
,
cosβ =![]() =
=
,
cosγ =
=
=
,
cosγ =![]() =
=![]() =
=![]() .
.
Т.о., сила = 8 действует в направлении вектора, образующего с координатными осями углы α = 60°, β = 60°, γ = 135°.
Скалярное произведение векторов
Скалярным произведением двух ненулевых векторов и (рис.3) называется число, равное произведению длин этих векторов на косинус угла φ между ними:
(
,![]() )
= |
|∙|
|∙
cos
φ.
(1)
)
= |
|∙|
|∙
cos
φ.
(1)
Обозначение: ( , ) или ∙ .
Рис.3.
Формулу (1) можно записать в виде:
(
,
)
= |![]() |∙
пр
|∙
пр![]() или |
|
∙ пр
или |
|
∙ пр![]() .
(2)
.
(2)
Из формул (2) имеем:
пр
=
![]() ,
пр
=
,
пр
=
![]() .
.
Свойства скалярного произведения:
1. ( , ) = ( , ).
2. (
,
(
+![]() ))
= (
,
)
+ (
,
).
))
= (
,
)
+ (
,
).
3. ((λ ), ) = λ ( , ).
4.
![]() =
|
|
– скалярный квадрат вектора
равен
квадрату его модуля.
=
|
|
– скалярный квадрат вектора
равен
квадрату его модуля.
5. Скалярное произведение векторов равно нулю тогда и только тогда, когда cos φ = 0 (φ = π/2) ( перемножаемые векторы перпендикулярны): ( , ) = 0 ┴ (или = , или
=
).
В частности: (![]() ,
)
= (
,
)
= (
,
)
= 0.
,
)
= (
,
)
= (
,
)
= 0.
Если векторы и заданы своими координатами
= {
ах,
ау,
аz
},
![]() = {
bх,
bу,
bz
}, то
(
,
)
= ах
bх
+ ау
bу
+ аz
bz
.
= {
bх,
bу,
bz
}, то
(
,
)
= ах
bх
+ ау
bу
+ аz
bz
.
Пример 11. Векторы
и
образуют угол φ =
![]() π.
Зная, что |
|
= 10 и |
|
= 2,
π.
Зная, что |
|
= 10 и |
|
= 2,
вычислить ( + 2 , 3 – ).
• Согласно свойствам скалярного произведения
( + 2 , 3 – ) = 3 ( , ) – ( , ) + 6 ( , ) – 2 ( , ) = 3 2 + 5 ( , ) – 2 2 =
= 3 | |2 + 5 | | | | cos φ – 2 | |2 = 3 100 + 5 10 2 – 2 4 = 300 – 50 – 8 = 242.
Пример 12. Дано: |
|
= 2, |
|
= 1, φ = (
)
=
![]() .
Найти модуль вектора
.
Найти модуль вектора
= 2 – 3 .
• Скалярный квадрат вектора : | |2 = 2 = ( , ) = (2 – 3 , 2 – 3 ) =
= 4 ( , ) – 6 ( , ) – 6 ( , ) + 9 ( , ) = 4 2 – 12 ( , ) + 9 2 =
= 4 |
|2
– 12
|
|
|
|
cos
φ + 9
|
|2
= 4
4
– 12
2 1
![]() +
9 1 =
= 16
– 12 + 9 = 13.
+
9 1 =
= 16
– 12 + 9 = 13.
Модуль вектора
:
|
|
=![]() .
.
Пример 13. Найти вектор
![]() ,
зная, что
,
= {1; 0; 1},
,
=
{0; 2; –1},
,
зная, что
,
= {1; 0; 1},
,
=
{0; 2; –1},
проекция вектора на вектор = {1; 2; 2} равна 1.
• Пусть вектор имеет координаты = {x; y; z}.
1) => ( , ) = 0 => x + z = 0;
2) => ( , ) = 0 => 2y – z = 0;
3) prc
= 1 =>
![]() = 1 => || |
|
=
= 1 => || |
|
=![]() =
3|| => x + 2y
+ 2z = 3.
=
3|| => x + 2y
+ 2z = 3.
Получили систему уравнений
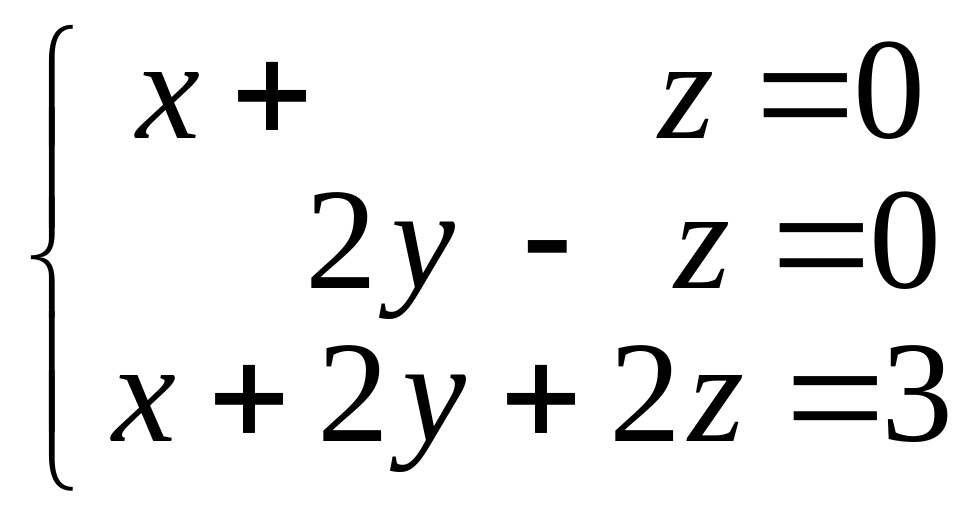 .
.
Решаем ее и находим: x
= –![]() ,
y =
,
y =
![]() ,
z =
.
Т.о.,
=
–
+
+
.
,
z =
.
Т.о.,
=
–
+
+
.
Пример 14. Даны вершины треугольника А (2; 3; –1), В (4; 1; –2), С (1; 0; 2). Найти:
а) внутренний угол при вершине С;
б)
![]() .
.
• а) Угол
φ при вершине С есть угол между векторами
![]() и
и
![]() .
Координаты этих векторов:
.
Координаты этих векторов:
={4 – 1; 1 – 0; –2 – 2} = {3; 1; –4}, ={2 – 1; 3 – 0; –1 – 2} = {1; 3; –3}.
Модули этих векторов: |
|
=![]() =
=
![]() ,
|
|
=
,
|
|
=
![]() =
=
![]() .
.
cos φ =![]() =
=
![]() =
=
![]() => φ = arccos
.
=> φ = arccos
.
б)
=
![]() =
=
![]() .
.
Пример 15.
Единичные векторы
![]() ,
,
![]() ,
,
![]() удовлетворяют условию
+
+
=
удовлетворяют условию
+
+
=
![]() .
.
Найти ( , ) + ( , ) + ( ).
• Последовательно умножим скалярно равенство + + = на , , :
(
,
)
+ (
,
![]() )
+ (
)
= 0,
)
+ (
)
= 0,
( , ) + ( , ) + ( ) = 0,
( , ) + ( , ) + ( ) = 0,
Сложим все три равенства. С учетом того, что ( , ) = ( , ) = ( ) = 1, получим 2(( , ) + ( , ) + ( )) = –3. Следовательно,
( , ) + ( , ) + ( ) = –1,5.
