
- •Общая электротехника и электроника учебно-методический комплекс
- •Методические указания к выполнению лабораторных работ
- •Направления подготовки бакалавров
- •I. Лабораторные работы на основе физических моделей общие указания
- •Охрана труда и техника безопасности
- •Рекомендации по выполнению лабораторных работ и оформлению отчета
- •Краткие сведения о применяемых в лаборатории электроизмерительных приборах и устройствах
- •Основные характеристики измерительных приборов
- •Работа 1. Исследование сложной электрической цепи постоянного тока
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Работа 2. Исследование линейных элементов электрических цепей
- •1. Цель работы
- •2. Основные теоретические положения
- •Фазовые соотношения между током и напряжением цепи
- •Амплитудные соотношения между током и напряжением цепи
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Работа 3. Исследование разветвленной цепи синусоидального тока с одним источником энергии
- •1. Цель работы
- •2. Основные теоретические положения
- •Расчет исследуемой цепи
- •Порядок расчета цепи с последовательно-параллельным соединением комплексных сопротивлений (рис. 3.1, а)
- •Порядок расчета цепи с параллельно-последовательным соединением комплексных сопротивлений (рис. 3.1, б)
- •Описание элементов исследуемой цепи
- •Экспериментальное исследование параметров цепи
- •Указания к построению векторных диаграмм
- •Указания к записи токов и напряжений в виде комплексных чисел
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Работа 4. Исследование частотных свойств цепи с последовательным соединением активного сопротивления, индуктивности и емкости
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Работа 5. Исследование трехфазной, соединенных по схеме «звезда»
- •1. Цель работы
- •2. Основные теоретические положения
- •Симметричный режим работы цепи при отсутствии нейтрального провода
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Работа 6. Исследование полупроводниковых диодов
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •1. Цель работы
- •2. Основные теоретические положения
- •Цепь rl при включении ее на постоянное напряжение u (поз. 1, табл. 7.1)
- •Цепь rl при отключении ее от постоянного напряжения u с одновременным замыканием накоротко (поз. 2, табл. 7. 1)
- •Цепь rс при отключении ее от постоянного напряжения u с одновременным замыканием накоротко (поз. 4, табл. 7.1)
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •1. Цель работы
- •Апериодический переходный процесс
- •Колебательный переходный процесс
- •Расчет сопротивления Rк и индуктивности l катушки по осциллограмме тока колебательного процесса
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Работа 9. Исследование явления феррорезонанса напряжений
- •1. Цель работы
- •2. Основные теоретические положения
- •Расчет вах феррорезонансной цепи
- •Анализ явления феррорезонанса
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •II. Лабораторные работы на основе компьютерного моделирования (виртуальные лабораторные работы) общие указания
- •Работа 1 (в). Исследование сложной электрической цепи постоянного тока
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Работа 2 (в). Исследование линейных элементов электрических цепей
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Работа 3 (в). Исследование разветвленной цепи синусоидального тока с одним источником энергии
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Работа 4 (в). Исследование частотных свойств цепи с последовательным соединением активного сопротивления, индуктивности и емкости
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Работа 5 (в). Исследование трехфазных цепей, соединенных по схеме «звезда»
- •Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •4. Cодержание отчета
- •5. Вопросы для самопроверки
- •Работа 6 (в). Исследование полупроводниковых диодов
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •1. Цель работы
- •2. Основные теоретические положения
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •1. Цель работы
- •3. Порядок выполнения работы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Методика применения программы Multisim для выполнения лабораторных работ общие положения
- •1. Назначение и состав программы Multisim
- •2. Открытие программы, ее составляющие и сборка схемы
- •Сборка схемы
- •3. Виртуальные измерительные приборы
- •Управление масштабом времени
- •Управление каналами а и в
- •Управление синхронизацией
- •III. Методические указания к выполнению лабораторных работ для студентов, занимающихся с элементами дот общие указания
- •Работа 10(д). Исследование линейных элементов
- •1. Цель работы
- •2. Основные теоретические положения
- •Фазовые соотношения между током и напряжением цепи
- •Амплитудные соотношения между током и напряжением цепи
- •3. Порядок выполнения работы
- •Виртуальные измерительные приборы
- •4. Содержание отчета
- •5. Вопросы для самопроверки
- •Исследование линейных элементов
- •Работа 2. Исследование переходных процессов в цепи с последовательным соединением активного сопротивления, катушки индуктивности и конденсатора
- •1. Цель работы
- •Апериодический переходный процесс
- •Колебательный переходный процесс
- •Расчет сопротивления r и индуктивности l по осциллограмме тока колебательного процесса
- •3. Описание лабораторной установки
- •4. Порядок выполнения работы
- •5. Содержание отчета
- •6. Вопросы для самопроверки
- •Исследование переходных процессов в цепи с последовательным соединением активного сопротивления, катушки индуктивности и конденсатора
- •Библиографический список
- •Содержание Виноградов Александр Леонидович Общая электротехника и электроника
- •Северо - Западный государственный заочный технический университет
- •191186, Санкт-Петербург, ул. Миллионная, д. 5
4. Содержание отчета
1. Схема исследуемой цепи и параметры элементов.
2. Технические и метрологические характеристики применявшихся измерительных приборов.
3. Таблицы с опытными и расчетными результатами.
4. Векторная диаграмма.
5. Выводы.
5. Вопросы для самопроверки
1. Как соотносятся между собой ток и напряжение в индуктивности; ток и напряжение в емкости?
2. Начальная фаза напряжения, приложенного к емкости, составляет +30. Какова начальная фаза тока в этой емкости?
3. Начальная фаза тока в индуктивности составляет 60. Какова начальная фаза напряжения, приложенного к этой индуктивности?
4. Сформулируйте первый и второй законы Кирхгофа применительно к векторам действующих токов и напряжений исследуемой цепи синусоидального тока.
5. К идеализированной катушке индуктивности приложено синусоидальное напряжение, действующее значение которого U = 314 B. Частота сети f = 50 Гц. Какова величина индуктивности этой катушки, если действующее значение тока в ней I = 1 A?
6. К идеализированному конденсатору приложено напряжение, действующее значение которого U = 318,5 B, угловая частота сети = 314 I/c. Какова величина емкости этого конденсатора, если действующее значение тока в нем I = 1 A?
7. Сформулируйте первый и второй законы Кирхгофа применительно к комплексным действующим значениям токов и напряжений исследуемой цепи синусоидального тока.
8.
К цепи, содержащей только индуктивное
сопротивление xL
= 2 Ом, приложено напряжение, комплексное
действующее значение которого
![]() .
Записать комплексное действующее
значение тока
в этом сопротивлении.
.
Записать комплексное действующее
значение тока
в этом сопротивлении.
9.
В цепи, содержащей только емкостное
сопротивление xC
= 1 Ом, протекает ток, комплексное
действующее значение которого
![]() .
Записать комплексное действующее
значение напряжения
,
приложенного к этой цепи.
.
Записать комплексное действующее
значение напряжения
,
приложенного к этой цепи.
Л и т е р а т у р а: [2], c. 29...43.
Работа 4. Исследование частотных свойств цепи с последовательным соединением активного сопротивления, индуктивности и емкости
1. Цель работы
Экспериментальное исследование резонанса и частотных характеристик цепи с последовательным соединением активного сопротивления, индуктивности и емкости.
2. Основные теоретические положения
Схема исследуемой цепи представлена на рис. 4.1, а. В соответствии со 2-м законом Кирхгофа для этой цепи имеем:
![]() .
(4.1)
.
(4.1)
Здесь
![]()
вектор действующего значения приложенного
напряжения;
вектор действующего значения приложенного
напряжения;
![]() вектор
действующего значения напряжения на
активном сопротивлении R
цепи, совпадающий по фазе с вектором
действующего значения тока
вектор
действующего значения напряжения на
активном сопротивлении R
цепи, совпадающий по фазе с вектором
действующего значения тока
![]() ;
;
![]() вектор
действующего значения напряжения на
индуктивном сопротивлении XL
= L
цепи, опережающий по фазе вектор
действующего значения тока
на 90;
вектор
действующего значения напряжения на
индуктивном сопротивлении XL
= L
цепи, опережающий по фазе вектор
действующего значения тока
на 90;
![]() вектор
действующего значения напряжения на
емкостном сопротивлении XC
= 1/
C
цепи, отстающий по фазе от вектора
действующего значения тока
на 90.
вектор
действующего значения напряжения на
емкостном сопротивлении XC
= 1/
C
цепи, отстающий по фазе от вектора
действующего значения тока
на 90.
Векторная диаграмма исследуемой цепи показана на рис. 4.1 для трех случаев соотношения между UL и UC.
На этой диаграмме векторы напряжений образуют прямоугольный треугольник со сторонами U, (UL UC) и UR. Из этого треугольника легко найти соотношения между действующими значениями напряжений и угол сдвига фаз между напряжением и током цепи:
![]() ;
(4.2)
;
(4.2)
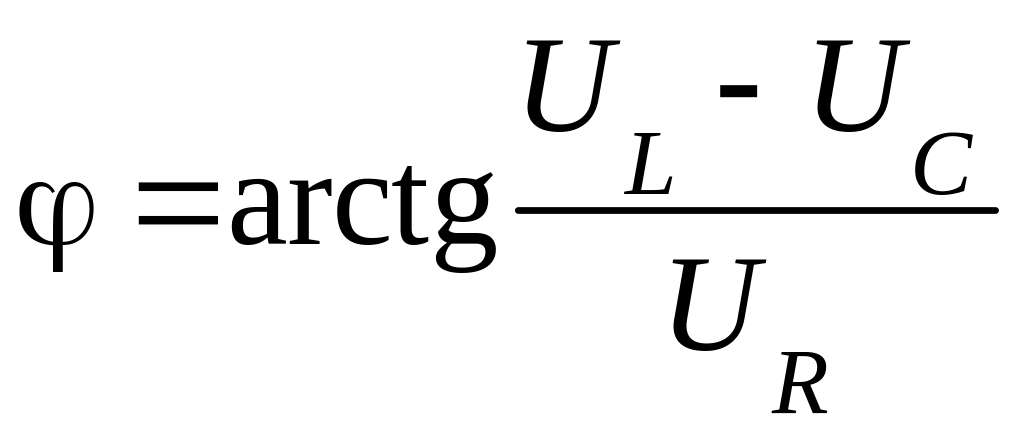 .
(4.3)
.
(4.3)

Р ис.
4.1
ис.
4.1
Рис. 4.2


Рис. 4.3
На рис. 4.1, б UL > UC ; ток цепи отстает по фазе от напряжения,
> 0 и цепь имеет индуктивный характер. На рис. 4.1, в UL < UC; ток цепи опережает по фазе напряжение, < 0 и цепь имеет емкостной характер. На рис. 4.1, г UL = UC; ток цепи совпадает по фазе с напряжением, = 0 и цепь имеет чисто активный характер. В этих условиях в цепи имеет место резонанс напряжений. При резонансе напряжений UL UC = 0 и U = UR.
Известно, что в соответствии с законом Ома
![]() ;
;
![]() ;
;
![]() .
(4.4)
.
(4.4)
Здесь
R
активное сопротивление цепи;
![]()
индуктивное сопротивление цепи;
индуктивное сопротивление цепи;
![]()
емкостное сопротивление цепи;
угловая частота цепи; f
частота цепи в герцах.
емкостное сопротивление цепи;
угловая частота цепи; f
частота цепи в герцах.
Подставив (4.4) в (4.2) и (4.3), получаем
![]() ,
(4.5)
,
(4.5)
где
![]()
полное сопротивление цепи.
полное сопротивление цепи.
 .
(4.6)
.
(4.6)
Из
соотношения
![]() вытекает, что при резонансе
вытекает, что при резонансе
![]() или
или
![]() .
Отсюда:
.
Отсюда:
![]() .
(4.7)
.
(4.7)
Это уравнение показывает соотношение между , L, C при резонансе. Если L и C заданные величины, то угловая частота цепи, при которой будет иметь место резонанс напряжений
![]() .
(4.8)
.
(4.8)
При
резонансе напряжений полное сопротивление
z
= R
и является минимальным, а ток в цепи
![]() при неизменном значении действующего
напряжения U
максимальным. Если при резонансе XL0
=
XC0
> R,
то напряжения на реактивных элементах
цепи больше приложенного к цепи
напряжения UL0
=
UC0
> U.
при неизменном значении действующего
напряжения U
максимальным. Если при резонансе XL0
=
XC0
> R,
то напряжения на реактивных элементах
цепи больше приложенного к цепи
напряжения UL0
=
UC0
> U.
Зависимости сопротивлений элементов цепи, напряжений на этих элементах, угла сдвига фаз, тока от частоты называются частотными характеристиками цепи. В данной работе рассматриваются зависимости активного сопротивления R, индуктивного сопротивления XL, емкостного сопротивления XC, полного сопротивления z, угла сдвига фаз и действующего значения тока цепи I от частоты приложенного напряжения. Общий вид этих характеристик показан на рис. 4.2.
При частоте 0 > преобладает емкостное сопротивление и цепь имеет емкостной характер ток опережает напряжение по фазе (векторная диаграмма на рис. 4.1, в).
При частоте > > 0 в цепи преобладает индуктивное сопротивление и цепь имеет индуктивный характер ток отстает от напряжения по фазе (рис. 4.1, б).
При частоте = 0 цепь является чисто активной ток и напряжение совпадают по фазе и наблюдается резонанс напряжений (векторная диаграмма на рис. 4.1, г).
При исследовании радиотехнических цепей широко используют понятие о характеристическом (волновом) сопротивлении , а также понятия о добротности Q, затухании d и абсолютной полосе пропускания (2 1) цепи.
Характеристическим (волновым) сопротивлением цепи называется сопротивление каждого из двух реактивных элементов исследуемой цепи при резонансе:
 .
(4.9)
.
(4.9)
Добротностью Q цепи (контура) с последовательным соединением
R, L, C называется отношение характеристического сопротивления к активному сопротивлению цепи
![]() .
(4.10)
.
(4.10)
Величина добротности показывает во сколько раз напряжение на индуктивности и емкости при резонансе превышает напряжение цепи.
Величина, обратная добротности, называется затуханием d
 .
(4.11)
.
(4.11)
