Министерство образования Российской Федерации

Уфимский государственный авиационный технический университет

Факультет ИРТ: Информатика и робототехника

Кафедра ПСИ: Проектирование систем информатики

Учебный курс:

СХЕМОТЕХНИКА

Комплект лабораторных работ:

ЦИФРОВАЯ СХЕМОТЕХНИКА

(комбинационные и последовательностные логические схемы)

Лабораторная работа ЛР2:

АНАЛИЗ, СИНТЕЗ И МИНИМИЗАЦИЯ ПРОСТЫХ КОМБИНАЦИОННЫХ СХЕМ

ОТЧЕТ

по лабораторной работе

Направление подготовки:

654600: ИВТ: Информатика и вычислительная техника

Специальность:

220300: САПР: Системы автоматизированного проектирования

Курс обучения: 3

Учебная группа: САПР-327

Работу выполнил

студент Абдрафиков М.А.

Зачетная книжка № 045135

Вариант задания: y810

Работу принял

ст. преподаватель Житников А.П.

2007

1. Анализ простой комбинационной схемы

(простое применение комбинационных логических элементов)

1. Исходное задание

Задана формула комбинационной логической функции:

СФО: Структурная формула объекта

y810= Nx2 V x3 & (Nx1 V Nx0 V x3 & Nx2 & x0) =

= Nx2 V (x3 & (Nx1 V (Nx0 V (x3 & (Nx2 & x0)))))

Введение промежуточных переменных

// для построений и контроля схемы

y810 = Nx2 V (x3 & (Nx1 V (Nx0 V (x3 & z1 )))) =

z1 = Nx2 & x0

= Nx2 V (x3 & (Nx1 V (Nx0 V z2))) =

z2 = x3 & z1

= Nx2 V (x3 & (Nx1 V z3)) =

z3 = Nx0 V z2

= Nx2 V (x3 & z4) =

z4 = Nx1 V z3

= Nx2 V (z5)

z5 = x3 & z4

Статический анализ комбинационной схемы

ЛС: Логическая схема системы анализа

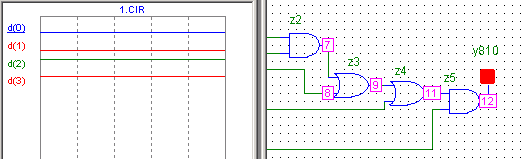
Схема без нумерации узлов

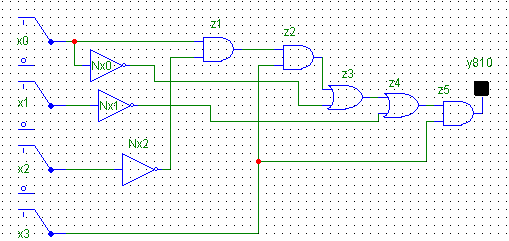
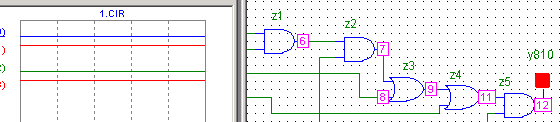
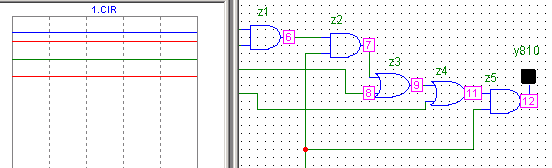
Нумерация узлов схемы

z2

z5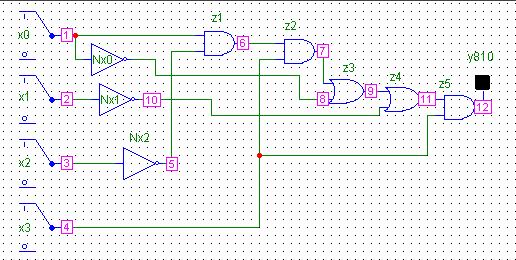

Нумерация узлов схемы и индикация состояний узлов

2. 

3. Функциональные соотношения

// Определяются на всех комбинациям состояний входов

// для построения таблицы истинности функции выхода

0: x3=0 x2 = 0 x1 = 0 x0=0 y = 0

1: x3=0 x2 = 0 x1 = 0 x0=1 y = 0

2: x3=0 x2 = 0 x1 = 1 x0=0 y = 0

3: x3=0 x2 = 0 x1 = 1 x0=1 y = 0

4: x3=0 x2 = 1 x1 = 0 x0=0 y = 0

5: x3=0 x2 = 1 x1 = 0 x0=1 y = 0

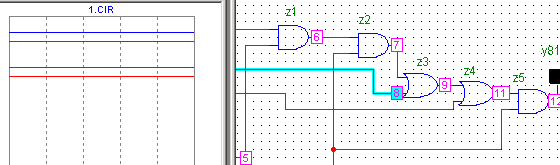
6: x3=0 x2 = 1 x1 = 1 x0=0 y =0

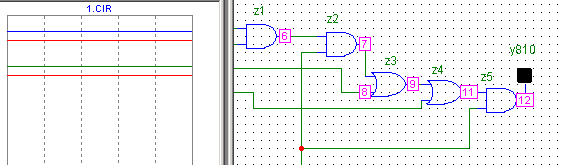
7: x3=0 x2 = 1 x1 = 1 x0=1 y = 0

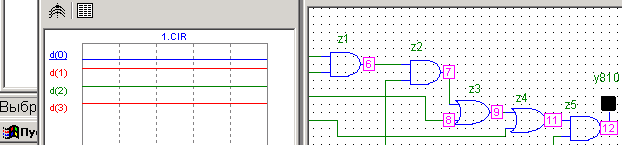
8: x3=1 x2 = 0 x1 = 0 x0=0 y = 1

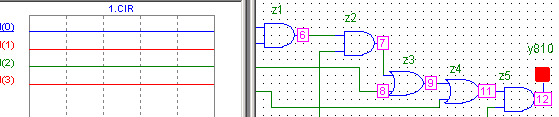
9: x3=1 x2 = 0 x1 = 0 x0=1 y =1

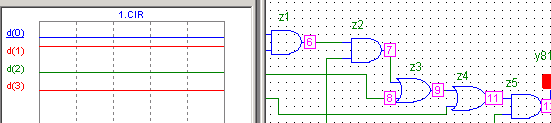
10: x3=1 x2 = 0 x1 = 1 x0=0 y =1

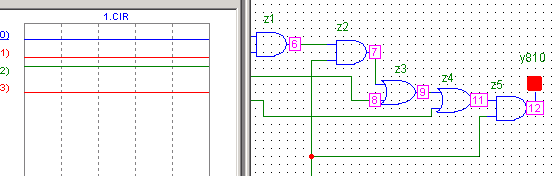
11: x3=1 x2 = 0 x1 = 1 x0=1 y = 1

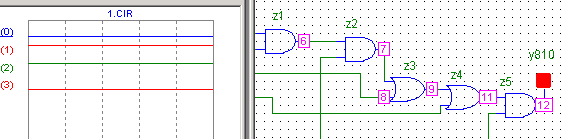
12: x3=1 x2 = 1 x1 = 0 x0=0 y = 1

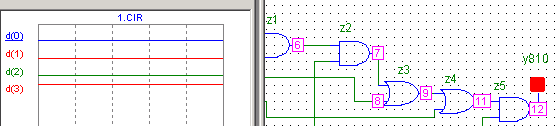
13: x3=1 x2 = 1 x1 = 0 x0=1 y = 1

14: x3=1 x2 = 1 x1 = 1 x0=0 y = 1

15: x3=1 x2 = 1 x1 = 1 x0=1 y = 0

ФТО: Функциональная таблица объекта

Форма 1

Гр.	№	x3	x2	x1	x0	y
1	0	0	0	0	0	0
	1	0	0	0	1	0
	2	0	0	1	0	0
	3	0	0	1	1	0
2	4	0	1	0	0	0
	5	0	1	0	1	0
	6	0	1	1	0	0
	7	0	1	1	1	0
3	8	1	0	0	0	1
	9	1	0	0	1	1
	10	1	0	1	0	1
	11	1	0	1	1	1
4	12	1	1	0	0	1
	13	1	1	0	1	1
	14	1	1	1	0	1
	15	1	1	1	1	0

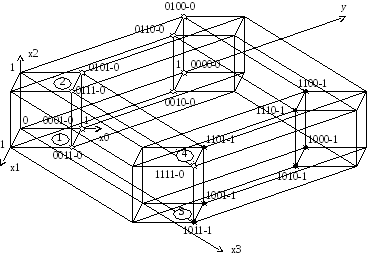
ФГО: Функциональный график объекта

(многомерный график размерности 5)

// для построений включить координатную сетку

1

ФВ: Функциональное (арифметическое) выражение

СФО: Структурная формула объекта / ИнФ: Инфиксная форма

y810= Nx2 V x3 & (Nx1 V Nx0 V x3 & Nx2 & x0) =

= Nx2 V (x3 & (Nx1 V (Nx0 V (x3 & (Nx2 & x0)))))

СФО: Структурная формула объекта /

ИнПрФ: Инфиксно-префиксная форма

= V (Nx2, (x3 & (Nx1 V (Nx0 V (x3 & (Nx2 & x0))))))=

= V (Nx2,(&(x3,(Nx1 V (Nx0 V (x3 & (Nx2 & x0)))))))=

= V (Nx2,(&(x3,( V (Nx1,(Nx0 V (x3 & (Nx2 & x0))))))))=

= V (Nx2,(&(x3,( V (Nx1,( V (Nx0, (x3 & (Nx2 & x0)))))))))=

= V (Nx2,(&(x3,( V (Nx1,( V (Nx0, (&(x3,(Nx2 & x0))))))))))=

= V (Nx2,(&(x3,( V (Nx1,( V (Nx0, (&(x3,( &(Nx2,x0)))))))))))

Замены обозначений

Y810= Max(Nx2,(Min(x3,(Max(Nx1,(Max(Nx0,(Min(x3,(Min(Nx2,x0))))))))))) =

=Max((1-x2),(Min(x3,(Max((1-x1),(Max((1-x0),(Min(x3,(Min((1-x2), x0)))))))))))

Динамический анализ работы комбинационной схемы

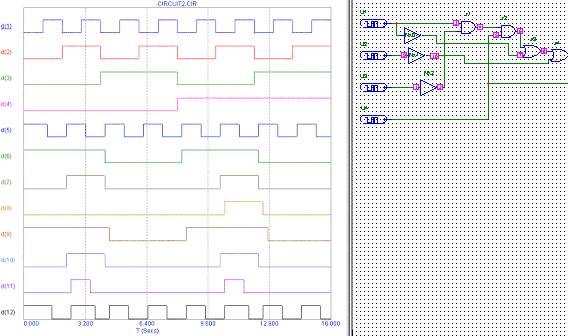
2. Синтез и минимизация простой комбинационной схемы

a → a135,

b → b135,

c → c135,

x → x135

y → y135

где 135 – последние три цифры в номере nnnABC зачетной книжки.

Синтез схемы по таблице истинности

Синтез схемы с доопределением функций по нулю

1. Таблица истинности

Вариант 1 доопределения таблицы истинности

abc	x	y
000 001 010 011 100 101 110 111	0 0 1 0 1 0 0 0	0 1 0 0 1 0 0 0

2. Синтез комбинационной схемы

Удобно проводить синтез по единичным условиям – мало единичных комбинаций.

Запись функций выходов в совершенной дизъюнктивной форме:

дизъюнкция всех единичных конъюнктивных комбинаций.

x = (Na & b & Nc) V (a & Nb & Nc)

y = (Na & Nb & c) V (a & Nb & Nc)

Соответствующая исходная схема – до ее минимизации

Вариант исполнения схемы в американском стандарте УГО

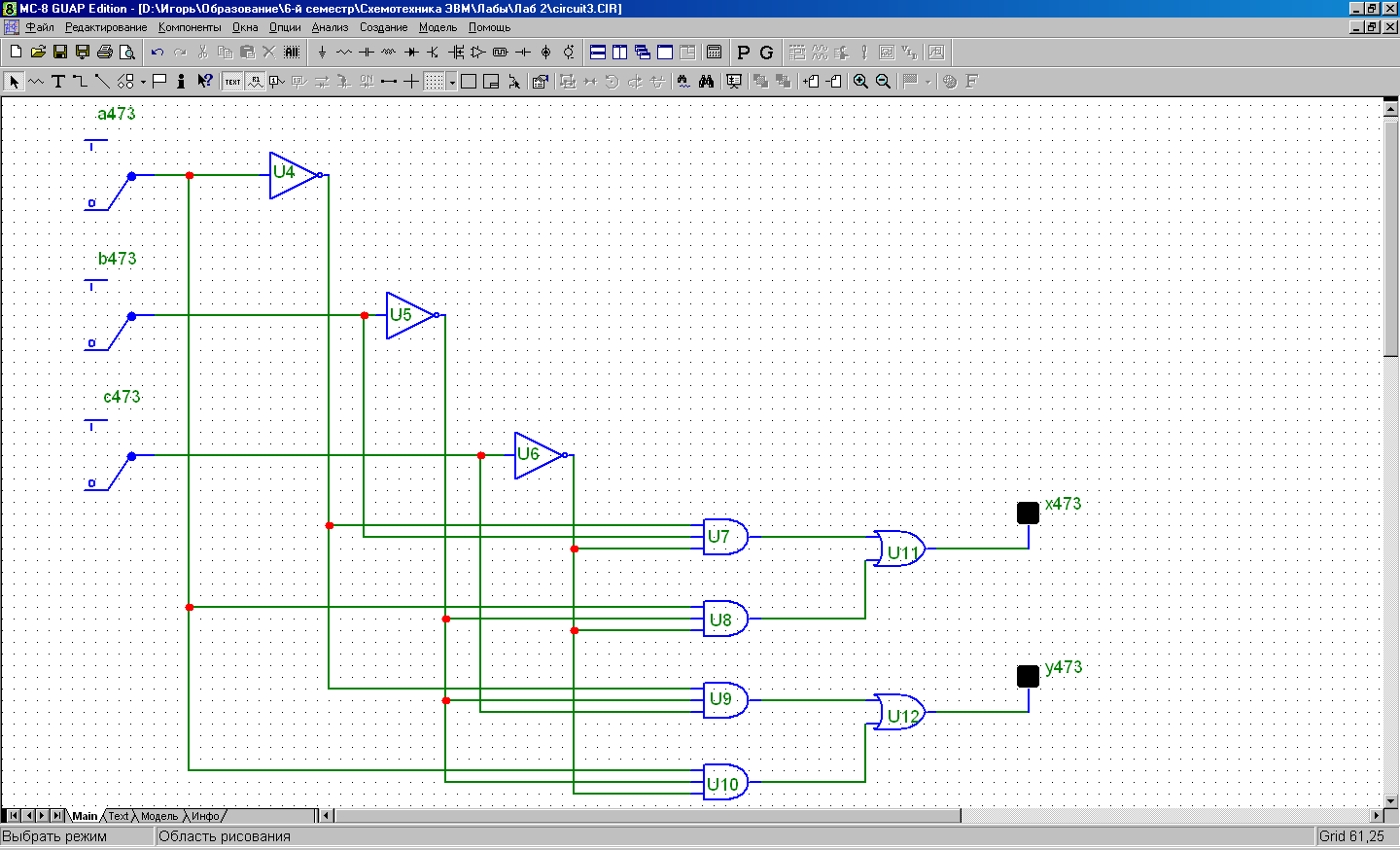
Вариант исполнения схемы в европейском стандарте УГО

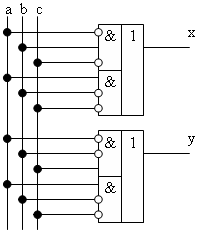
3. Проверка работы схемы

Проверяются только заданные комбинации:

Условие:

abc = 000 xy = 00

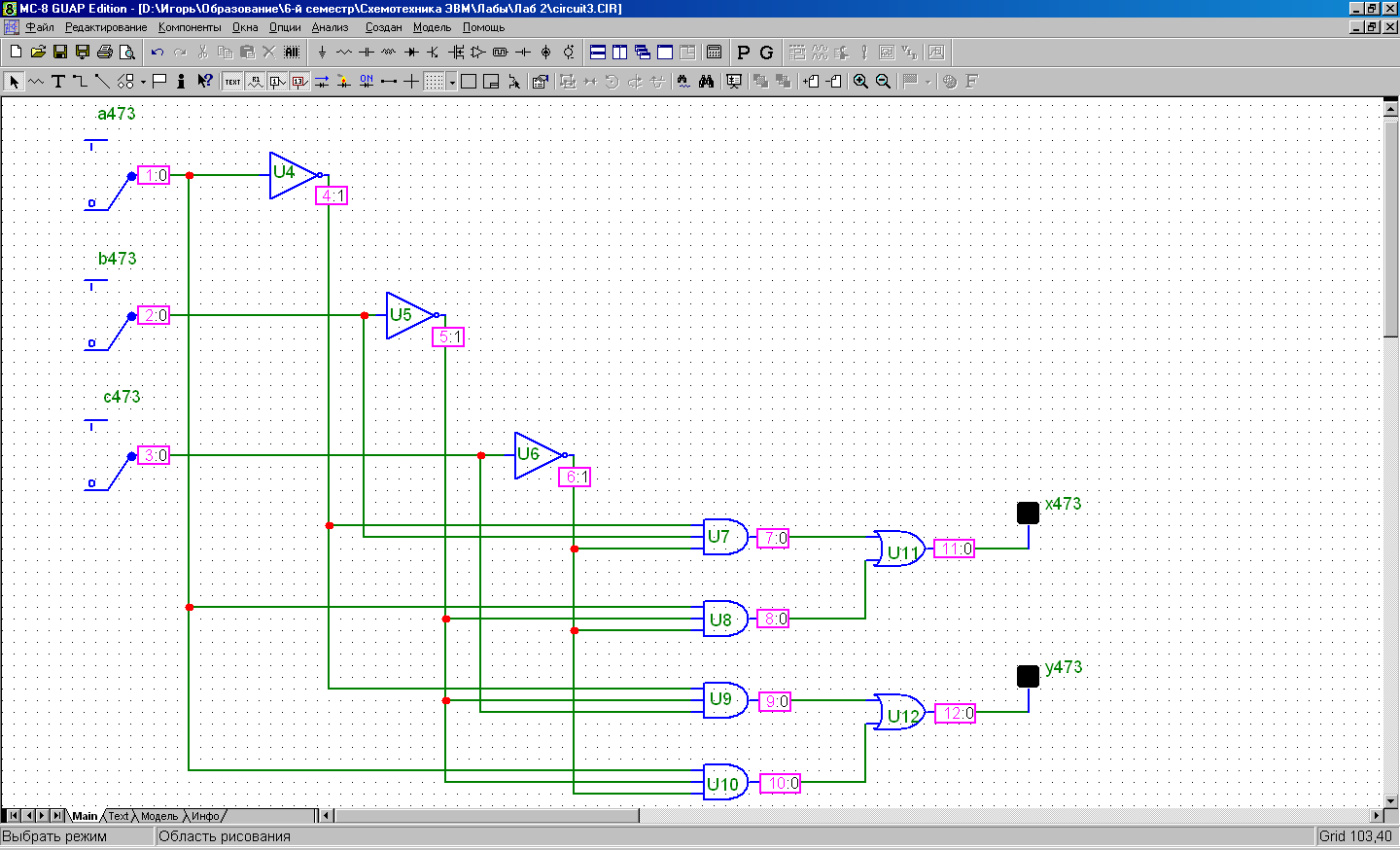
Условие

abc = 001 xy = 01

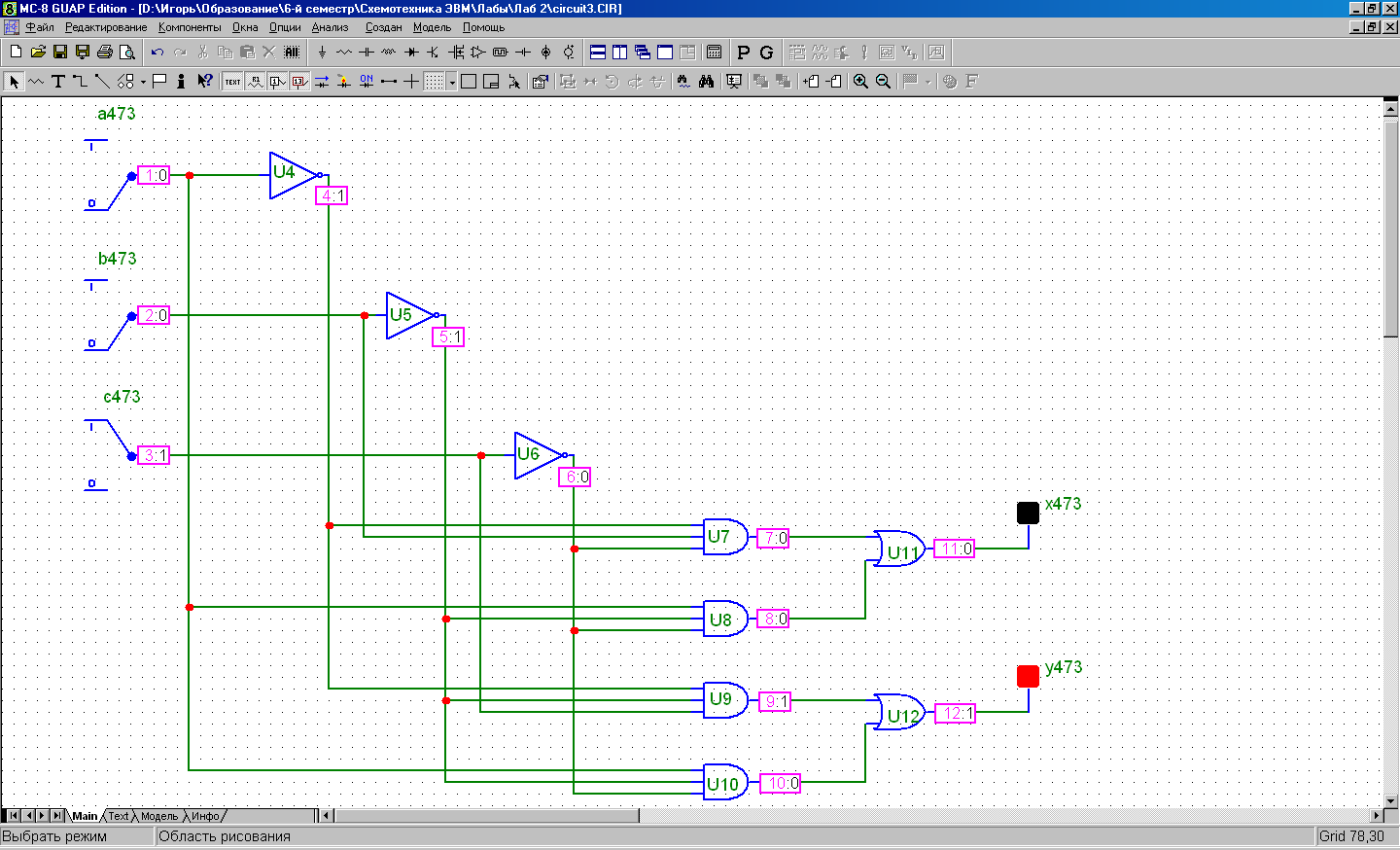
Условие

abc = 010 xy = 10

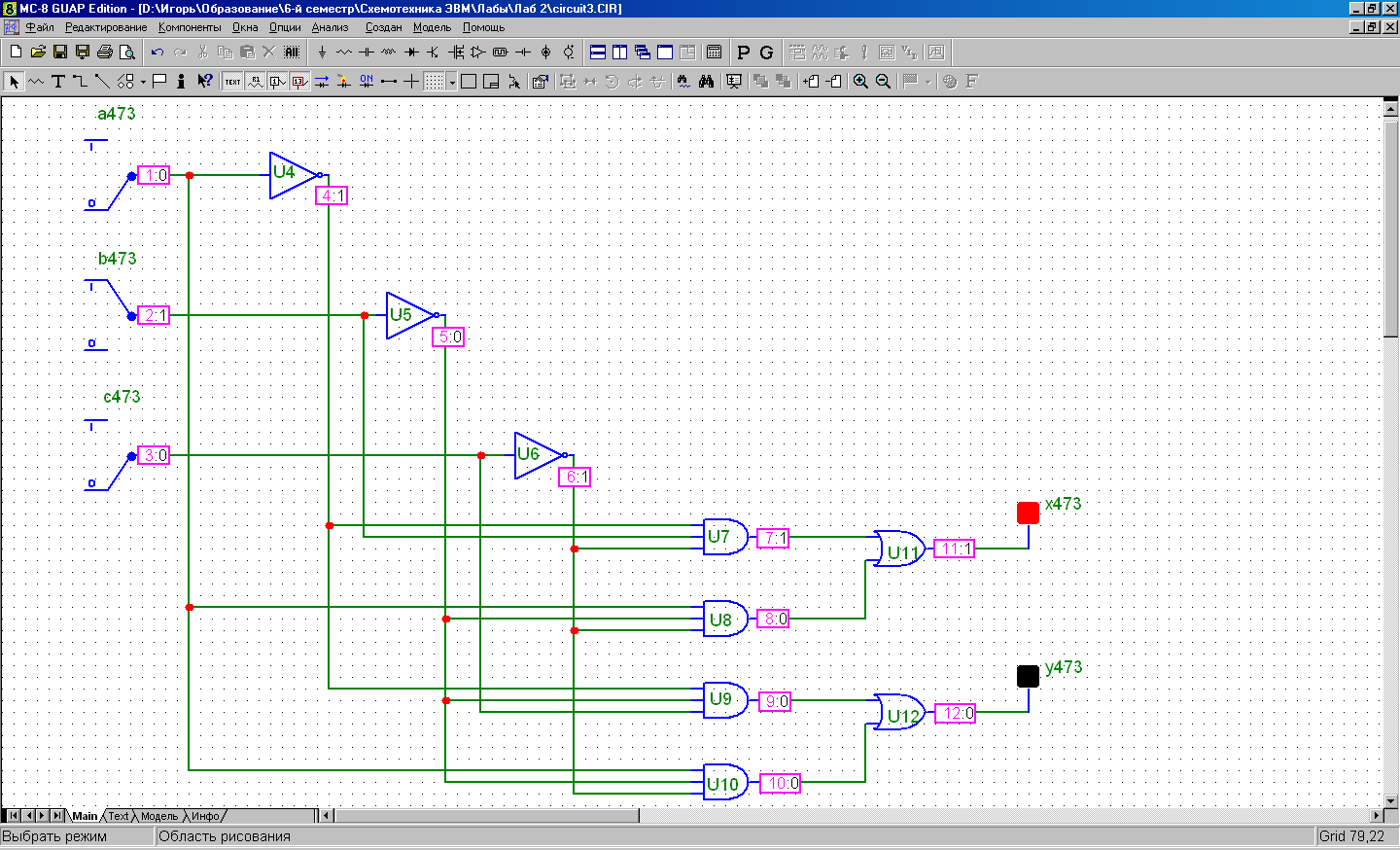
Условие

abc = 100 xy = 11

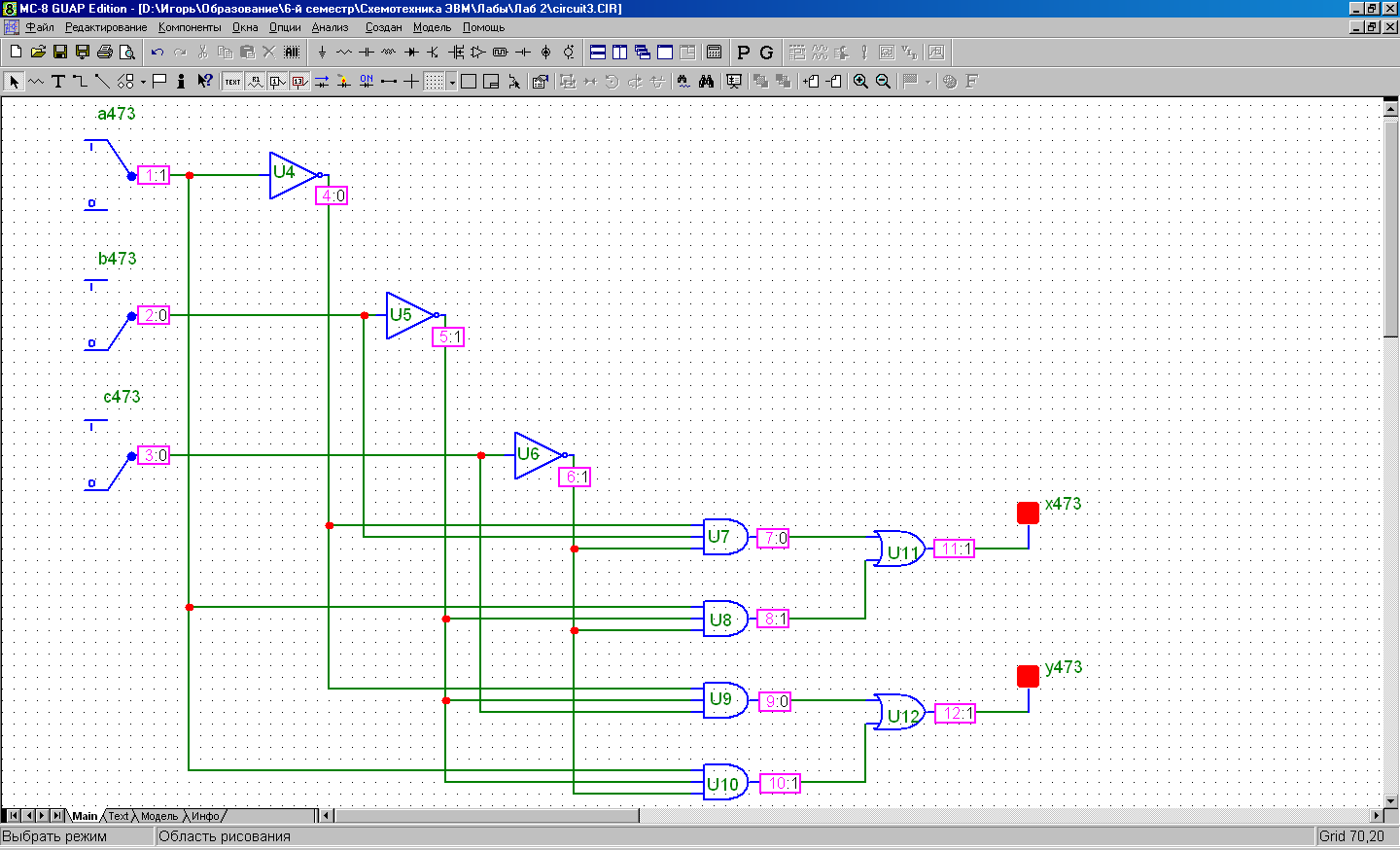
Заключение:

заданные условия выполняются.

Синтез схемы с доопределнием функций по единице

4. Таблица истинности

Вариант 2 доопределения таблицы истинности:

abc	x	y
000 001 010 011 100 101 110 111	0 0 1 1 1 1 1 1	0 1 0 1 1 1 1 1

Общая логическая схема – намного проще:

x473 = a473 V b473

y473 = a473 V c473

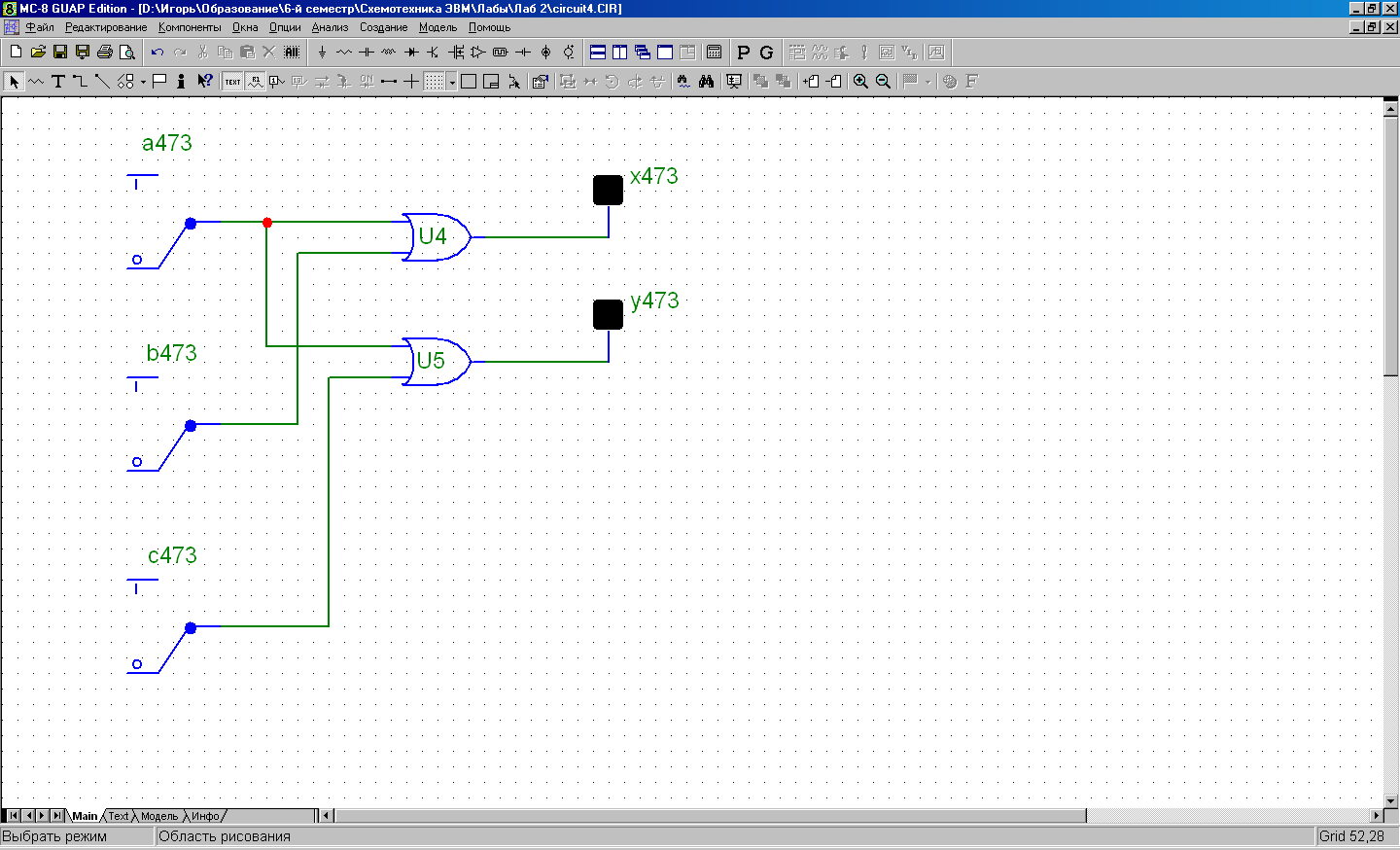
11. Проверка работы схемы

Проверка заданных комбинаций:

abc = 000 xy = 00

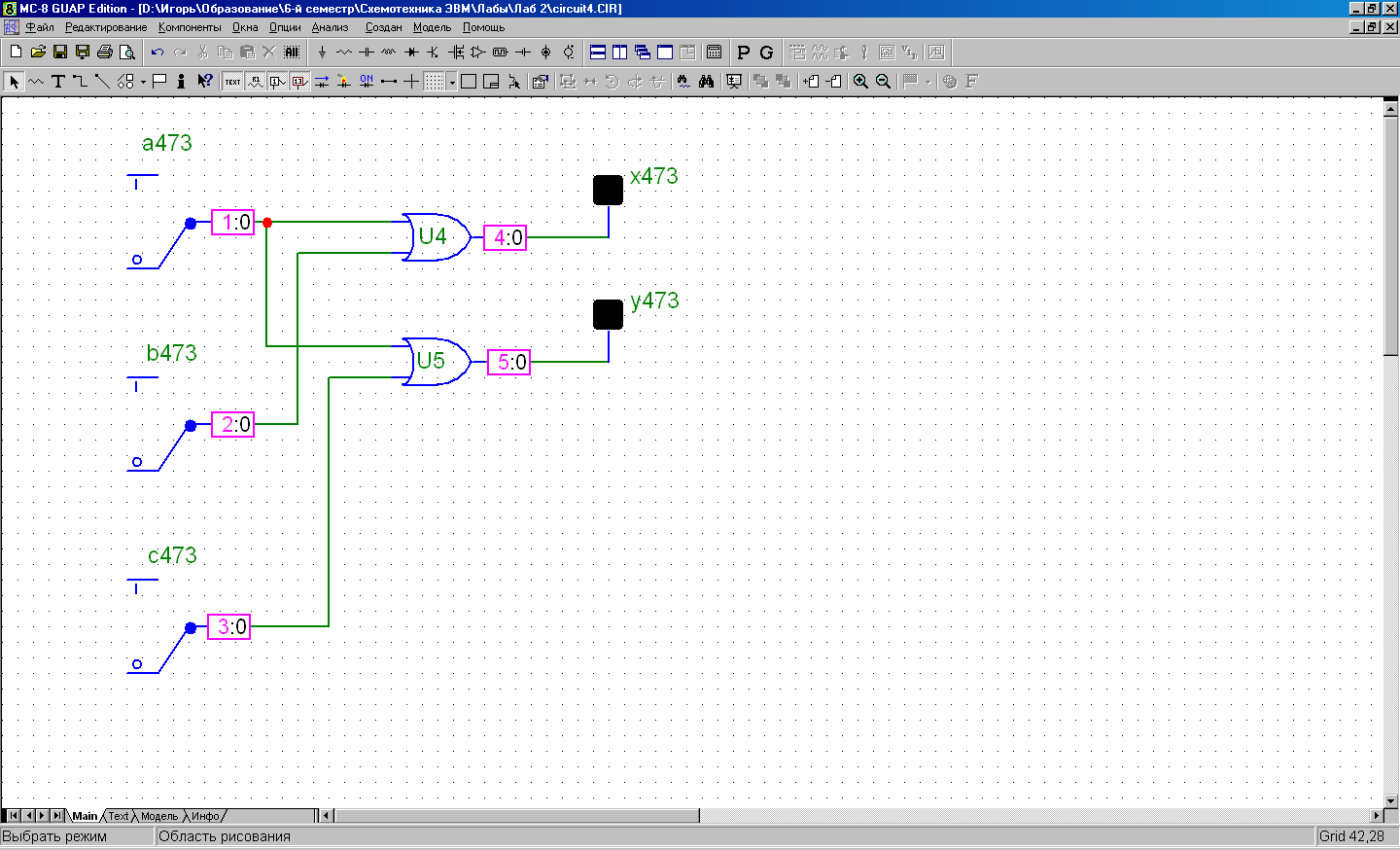
abc = 001 xy = 01

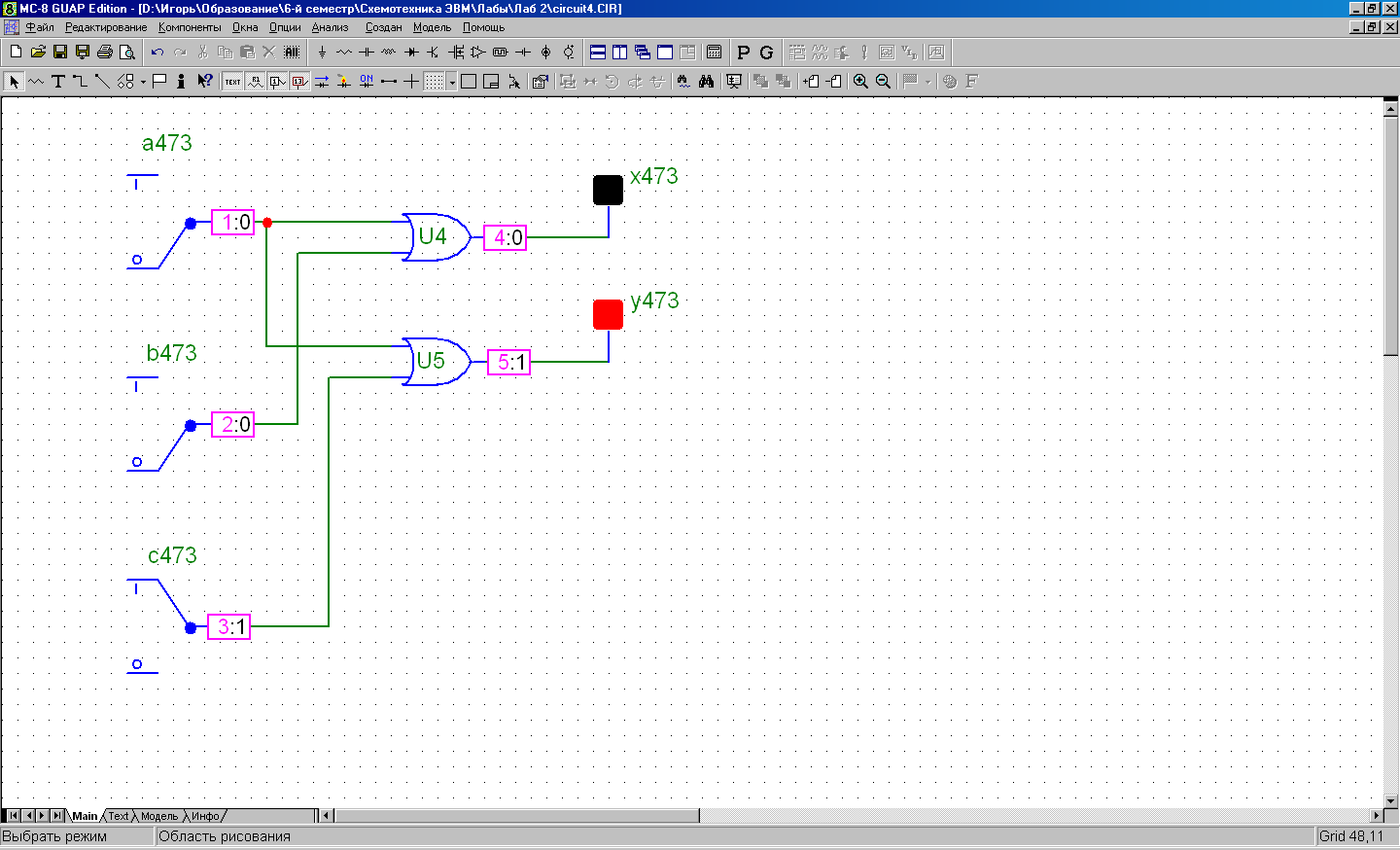
abc = 010 xy = 10

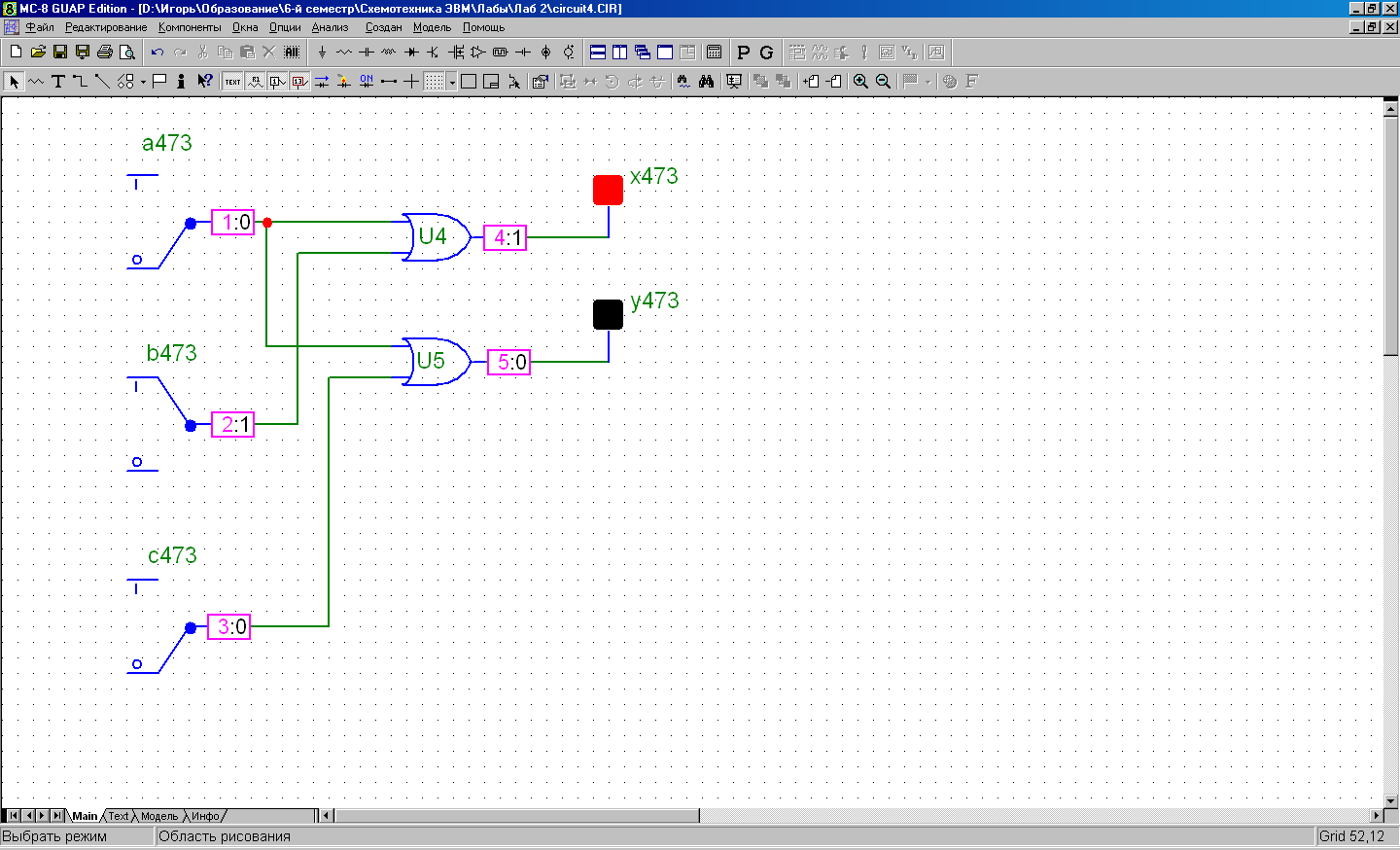
abc = 100 xy = 11

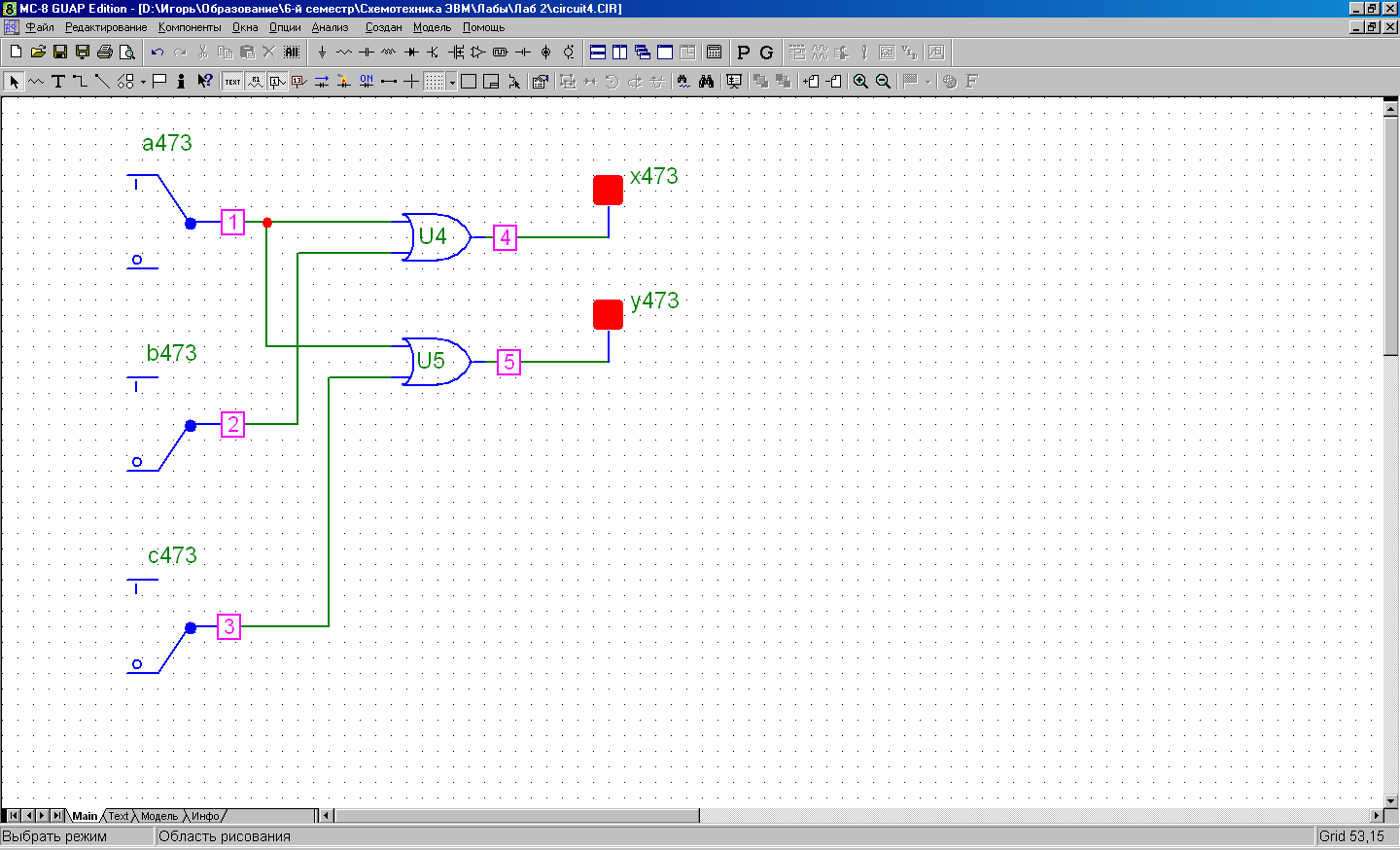
Выполнение индивидуального задания

Исходные условия

12. Заданная функция

y250 = Nx0 V (x1 & Nx2 & x3 V Nx2) & x1 & Nx0 =

= Nx0 V (((((x1 & Nx2) & x3) V Nx2) & x1) & Nx0)

13. Таблица истинности

Гр.	x3	x2	x1	x0	y
1	0	0	0	0	1
	0	0	0	1	0
	0	0	1	0	1
	0	0	1	1	0
2	0	1	0	0	1
	0	1	0	1	0
	0	1	1	0	1
	0	1	1	1	0
3	1	0	0	0	1
	1	0	0	1	0
	1	0	1	0	1
	1	0	1	1	0
4	1	1	0	0	1
	1	1	0	1	0
	1	1	1	0	1
	1	1	1	1	0

Минимизация формулы методом Карно

14. Таблицы Карно

Исходная таблица Карно:

y = F(x3, x2, x1, x0)
	x0		Nx0
x3	1	1	0	0	x1
Nx3	1	1	0	0
	1	1	0	0	Nx1
x3	1	1	0	0
	x2	Nx2		x2

Покрытие полей единиц:

Синтез сокращенной функции:

y = F(x3, x2, x1, x0)
	x0		Nx0
x3	0	0	1	1	x1
Nx3	0	0	1	1
	0	0	1	1	Nx1
x3	0	0	1	1
	x2	Nx2		x2

y250 = Nx0

15. Анализ результатов

Получена функция:

y250 = Nx0

Переменные:

1 вхождение переменной

инверсное для Nx0

Операции:

нет

Исходная функция – для сравнения

y250 = Nx0 V (x1 & Nx2 & x3 V Nx2) & x1 & Nx0

Выводы

Получен не минимальный вариант формулы и схемы.

Исходная формула представляется более минимальный вариант (относительно совершенной дизъюнктивной нормальной формы).

20