
Інтерференція світла приклад розв’язування задач
Задача 1
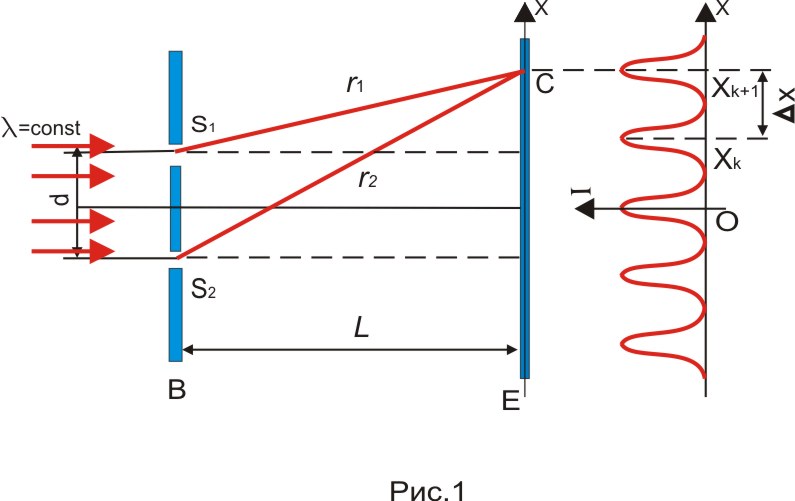
На діафрагму з двома вузькими щілинами, які знаходяться на віддалі d, падає нормально монохроматичний пучок світла з довжиною хвилі . Інтерференційна картина спостерігається на екрані, що знаходиться на віддалі L (дослід Юнга).
а) Яка відстань х між найближчими максимумами?
б) Знайти розподіл інтенсивності на екрані у цьому досліді.
в) На яку віддаль і у якому напрямку змістяться інтерференційні смуги, якщо одну із щілин закрити скляною пластинкою товщиною h з показником заломлення n?
Розв’язання
а) Відстань між сусідніми максимумами це величина, яку можна визначити з рівності
![]()
 ,
(1)
,
(1)
де
![]() і
і
![]()
координати відповідно k+1
та k
максимуму.
координати відповідно k+1
та k
максимуму.
Умова максимуму при інтерференції:
![]() ,
(2)
,
(2)
де
r2
і r1
оптична різниця ходу у випадку, якщо
![]() .
.
Шукатимемо
різницю
![]() .
Як видно з рис. 1
.
Як видно з рис. 1
![]() ,
,
![]()
![]()
![]()
Враховуючи,
що
![]() вважатимемо, що r2+r12L.
Тоді:
вважатимемо, що r2+r12L.
Тоді:
![]() (3)
(3)
Отже, різниця ходу дорівнює
![]() (4)
(4)
Для
максимуму інтерференції координату
хmax
знайдемо враховуючи (4) і (2)
![]() .
.
Згідно
з (1) для х
одержуємо
![]() .
.
Отже:
![]() (5)
(5)
б)
Розподіл інтенсивності знайдемо
використовуючи вираз
![]() ,
,
де різниця фаз величина, яка визначається з рівності:
![]() (6)
(6)
Враховуючи (4) маємо
![]() (7)
(7)
Оскільки
I1=I2=I0,
то
![]() ,
де
,
де
![]() і остаточно:
і остаточно:
![]() (8)
(8)
в) Якщо один із променів перекрити тонкою прозорою пластинкою, то це спричинить зміну оптичної різниці ходу променя (наприклад 1), див. рис. 2.
Ця
зміна призведе до того, що максимум
інтерференційної картини з точки С(х1)
зміститься у деяку іншу точку С(х2).
А тому у випадку, коли пластинка відсутня,
згідно з (4)
![]() .
.
Коли
пластинка перекриває промінь 1 матимемо
![]() .
.
Величина S=x2x1 і визначатиме віддаль, на яку змістилась інтерференційна картина.
Із рис. 2 бачимо, що
![]() ,
,
або:
![]() (9)
(9)
Враховуючи
(4) одержимо
![]()
![]() ,
звідки
,
звідки
![]() .
.
Отже,
![]() (10)
(10)
Знак () вказує на те, що координата x1>x2. Отже точка С знаходитиметься ближче до т. О, див. рис. 2.
Задача №2
Спочатку вертикальну мильну плівку спостерігають у відбитому світлі через червоне скло (λ1=6,3·10-7 м). При цьому відстань між сусідніми червоними смугами дорівнювала 3 мм. Потім цю плівку спостерігають через синє скло (λ2 = 4·10-7 м). Знайти відстань між сусідніми синіми смугами. Вважати, що форма плівки за час спостереження не змінюється.
Д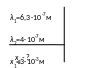
 ано: Розв’язання
ано: Розв’язання
У око спостерігача потрапляють промені, відбиті від тонкого клину перпендикулярно його поверхні. Тоді для k-ої і (k+1)-ої червоних смуг оптичні різниці ходу відповідно рівні
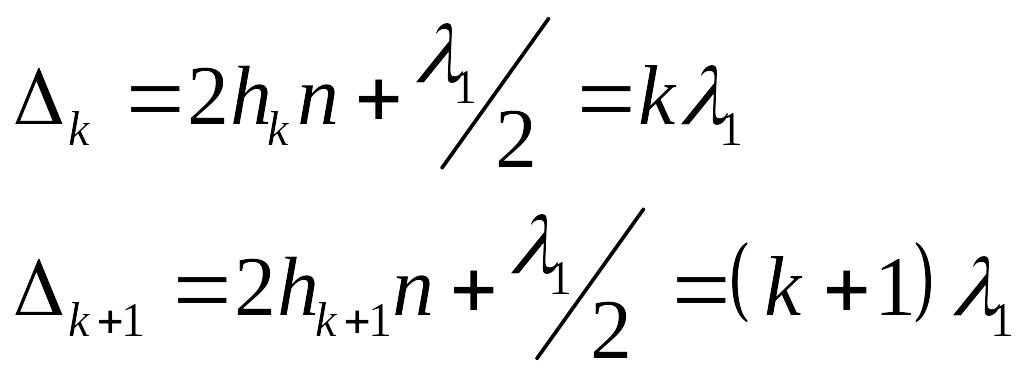 (1)
(1)
(![]() у
обох випадках, де r
кут падіння). Тут hk
і hk+1
– товщини
вертикальної мильної плівки
у місцях, де спостерігаються відповідні
смуги.
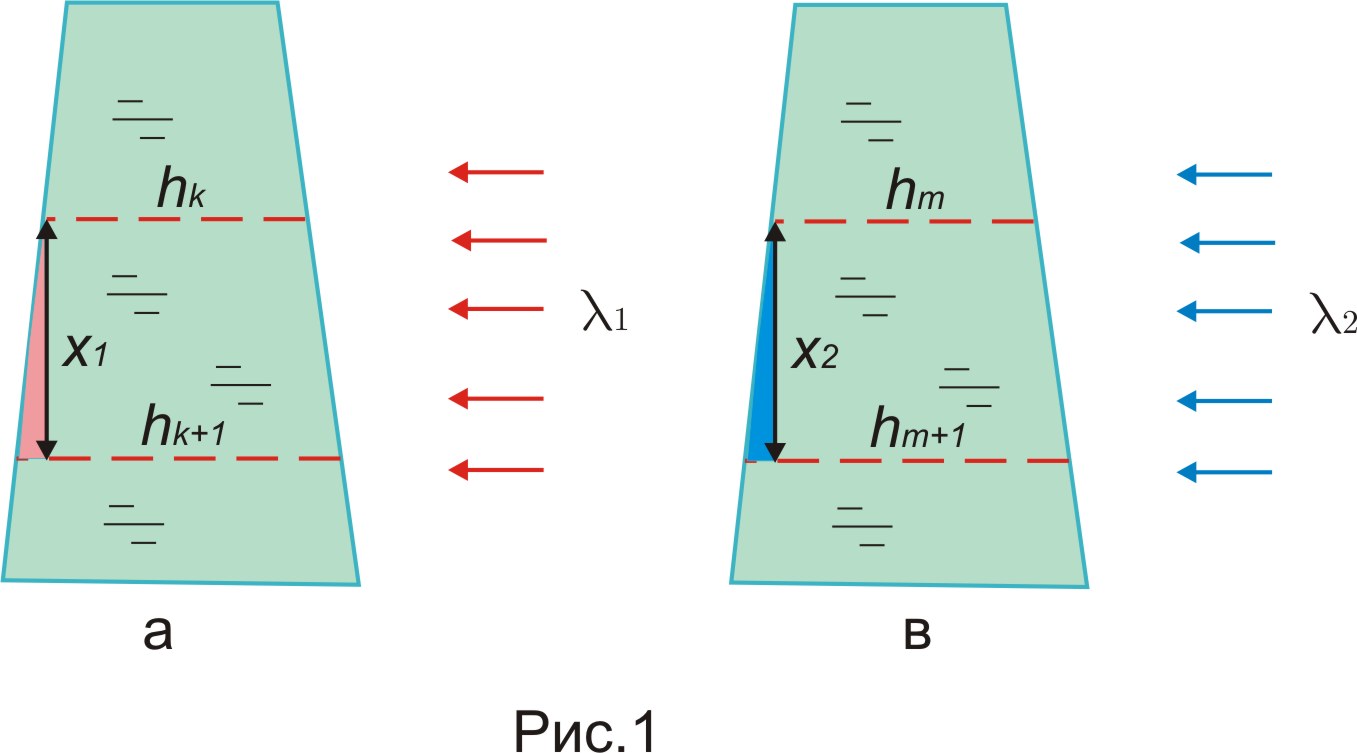
Поперечний перетин плівки являє собою
клин (рис. 1 а). З виразів (1) знаходимо
у
обох випадках, де r
кут падіння). Тут hk
і hk+1
– товщини
вертикальної мильної плівки
у місцях, де спостерігаються відповідні
смуги.
Поперечний перетин плівки являє собою
клин (рис. 1 а). З виразів (1) знаходимо
![]()
звідки
![]() (2)
(2)
Аналогічно, для синіх смуг (рис. 1 в).
![]() (3)
(3)
Розділивши почленно вирази (2) й (3), одержимо
![]() (4)
(4)
Інакше, з подібності заштрихованих трикутників (мал. 1а,б) виходить
![]()
Прирівнюючи праві частини рівнянь (4) й (5), знаходимо
![]() І
остаточно маємо:
І
остаточно маємо:
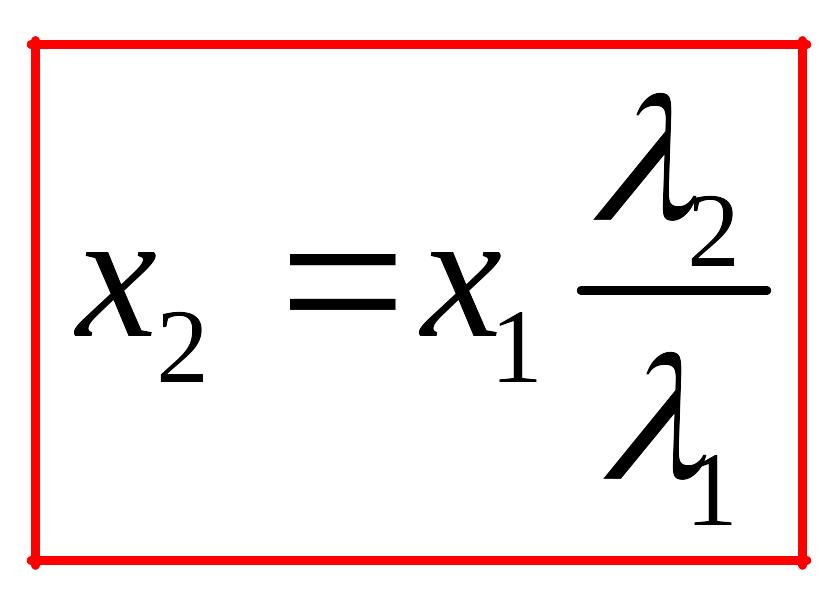
Підставляючи числові значення одержимо:
![]()
Відповідь:
![]()
Задача №3
Установка для спостереження кілець Ньютона освітлюється монохроматичним світлом, довжина хвилі якого λ = 675 нм, що падає нормально до пластинки. Відстань між 5-м і 25-м світлими кільцями Ньютона Δr = 9 мм. Визначити радіус кривизни R опуклої лінзи, якщо спостереження проводять у відбитому світлі.
Дано: Розв’язання.
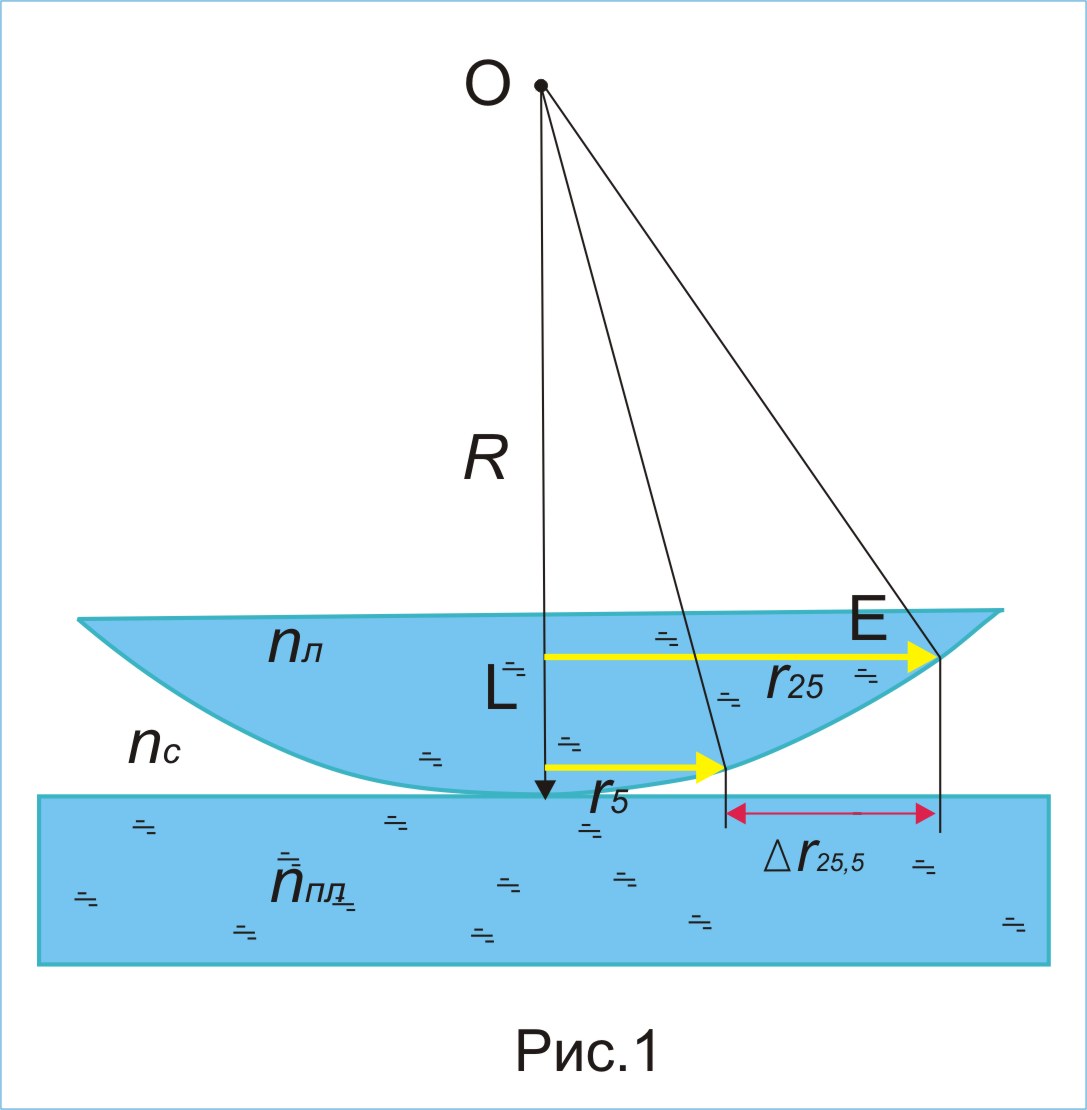

Із
![]() (рис. 1) маємо:
(рис. 1) маємо:
![]() ,
або
,
або
![]() ,
звідкіля
,
звідкіля
![]() .
.
Нехтуючи
малою величиною h2
у порівнянні з іншими доданками, одержуємо
![]() .
Для
світлого
i-го
кільця у відбитому світлі різниця ходу
визначається як
.
Для
світлого
i-го
кільця у відбитому світлі різниця ходу
визначається як
![]() звідки
звідки![]() .
Тоді
.
Тоді
![]()
Для k = 5 і k = 25 маємо
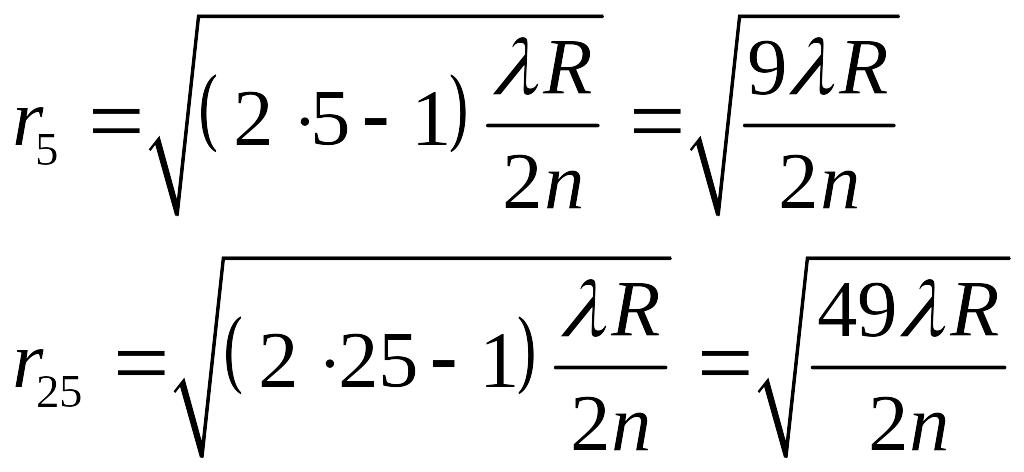
Тоді
![]() ,
,
![]()

![]()
Відповідь: Радіус лінзи R = 15 м
Задача 4.
Визначити товщину тонкої плівки олії на поверхні води, якщо при спостереженні через спектроскоп під кутом 600 до нормалі в спектрі відбитого світла видно підсилену жовту лінію = 0,589 мкм. Показник заломлення олії n = 1,47.
Розв’язання.
n = 1,47 = 0,589 мкм
d -? |
Умова
максимуму у відбитому від плівки
світлі
|
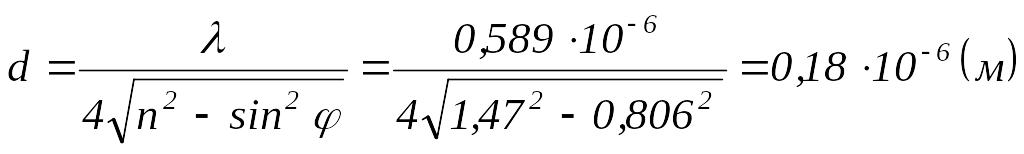


 Дано:
Дано: