Фотометрія

ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ

Задача 1. Електрична лампа розжарення потужністю N = 40 Вт випромінює світловий потік Ф_л = 415 лм. Вона підвішена на висоті h - 1,5 м над центром круглого стола діаметром D = 2 м. Визначити світлову віддачу лампи, силу світла джерела, освітленість у центрі і на краю стола (рис. 2).

Р озв’язування

Світлова віддача лампи

Сила світла

Освітленість у центрі стола оскільки кут падіння дорівнює нулеві

Освітленість на краю стола 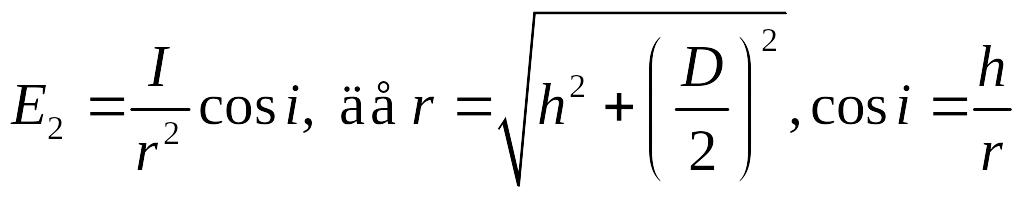тому остаточно маємо:

Відповідь: , , ,

Задача 2. На столі лежить книга на відстані L від основи перпендикуляра, проведеного з електричної лампи до площини стола. Лампа може лише підійматися й опускатися (її можна вважати точковим джерелом). На якій висоті h над столом слід підвісити лампу, щоб освітленість книги була максимальною?

Розв'язування.

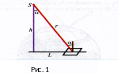Нехай сила світла, що випромінюється лампою, дорівнює І. Обчислимо освітленість книги як функцію висоти h лампи над столом. Як видно з рис. 1, відстань джерела світла від книги . За формулою освітленості Оскільки то остаточно отримаємо: Дослідивши цей вираз для на екстремум, знайдемо:

Відповідь:

Задача 3. Точкове джерело s, сила світла якого I = 50 кд, знаходиться над поверхнею стола на висоті h = 1 м (рис. 3). Знайти освітленість у точці М, в яку промені джерела s потрапляють перпен­дикулярно. Як зміниться освітленість у точці М, якщо збоку від s на відстані l = h розмістити плоске дзеркало Z, яке відбиває світло в точку М? Вважати, що коефіцієнт відбивання дорівнює 1.

Р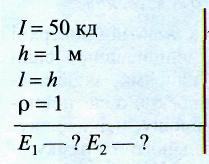 озв’язування

Освітленість у точці М за відсутності дзеркала

Після встановлення дзеркала Z у точку М потраплятимуть також промені, відбиті від дзеркала. Освітленість у точці М створюватиметься немовби двома джерелами світла: справжнім s і уявним s'.

За коефіцієнта відбивання, що дорівнює 1, уявне джерело s' має таку саму силу світла, як і джерело s. Отже, додаткова освітленість у точці М буде

де r = OM+Os'; і = 45° (за побудовою).

З ∆ sOs' бачимо, що Os = Os' (як сторони рівнобедреного трикутника). Оскільки за побудовою Os = sM, то Os' = sM. 3 ∆ OsM знаходимо:

Отже,

Піднесемо до квадрата ліву і праву частини цього виразу:

Повна освітленість у точці М дорівнює сумі освітленостей Е₁ і Е_д:

Відповідь: ,

ГЕОМЕТРИЧНА ОПТИКА

ПРИКЛАДИ РОЗВ'ЯЗУВАННЯ ЗАДАЧ

Задача 1. Висота палі залізного моста, який будується, 10 м. Глибина водойми 6 м. Яка довжина тіні палі на дні водойми, якщо сонячні промені па дають під кутом а = 40° до горизонту?

Р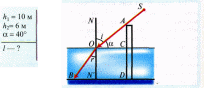 озв 'язування

Довжина тіні DB = l складається з довжини тіні ОС надводної частини палі АС і довжини тіні BN' підводної частини палі CD (рис.1). З прямокутного трикутника ∆АСО випливає, що

де і - кут падіння променя, що дорівнює 90° - α.

Довжину підводної частини тіні знайдемо з ∆ОN’B:

,

де r - кут заломлення сонячного променя на поверхні води в точці О.

Отже, довжина тіні палі

Кут r знайдемо за формулою закону заломлення світла:

Тоді

Відповідь: l = 9м.

Задача 2. Кут заломлення призми ψ = 45°. Монохроматичний промінь світла падає на бічну грань призми під кутом i = 30°. Знайти кут відхилення про­меня, якщо показник заломлення матеріалу призми n=1,6.

Розв'язування

Н ехай на ліву грань падає промінь SA (рис. ). Тут він заломлюється і йде в напрямку АВ. У точці В промінь заломлюється вдруге і йде в напрямку BS^’.

Продовжимо промені SA і BS^’ до їх перетину в точці С. Кут φ, утворений перетином продовження променя, що падає на призму, і продовження променя, що виходить із призми (кут відхилення призми), потрібно визначити.

З ∆AВС випливає, що . Однак із рис. видно, що тому . З ∆АВD бачимо, . Тому . З урахуванням сказаного кут відхилення променя мож­на визначити за виразом

Щоб знайти г І, застосуємо послідовно закон заломлення світла до першої і другої граней призми:

, відповідно r =18^º

З трикутника АВD тому

Отже: r₁=46º.

Підставляючи одержані значення у формулу для кута відхилення променя знайдемо:

Відповідь:

Задача 3.

Радіус кривизни вгнутого сферичного дзеркала r = 40 см. Знайти положення об'єкта, при якому: а) зображення дійсне і збільшене в два рази; б) уявне і збільшене в два рази.

Дано:

Р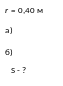 озв'язання.

Згідно з формулою (11), збільшення сферичного дзеркала Оскільки дійсне зображення, що його дає вгнуте дзеркало, завжди обернене, то при а) , тобто або Той факт, що S і S' мають однакові знаки, якраз і означає, що об'єкт і його дійсне зображення лежать по один бік від вершини дзеркала. Тоді на підставі рівняння (25): , звідки шукана відстань . У випадку б) , бо уявне зображення, що його дає вгнуте дзеркало, завжди пряме. Отже, , тобто . Тоді , або , звідки .

Задача 4.

Головна фокусна відстань лінзи для жовтого променя f_ж = 80 см. Яка головна фокусна відстань лінзи для червоного і фіолетового променів? Показники заломлення цих променів відповідно дорівнюють: п_ч - 1,602; п_ж = 1,610; n_ф - 1,650.

Разв 'язування

З апишемо формулу лінзи для жовтого і червоного променів:

Взявши відношення виразів (а) і (б), дістанемо звідки

Аналогічно знайдемо головну фокусну відстань лінзи для фіолетового променя

Відповідь: ,

Задача 5.

Знайти збільшення, яке можна одержати за допомогою лупи, якщо її фокусна відстань 2 см: для нормального ока з відстанню найкращого бачення L = 25 см; для короткозорого ока з відстанню найкращого бачення L₁ - 15 см.

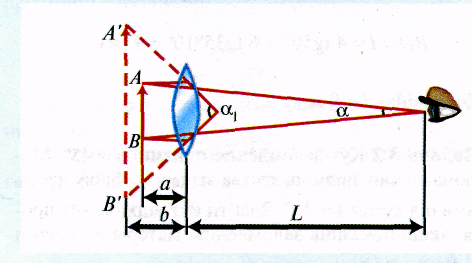Розв'язування

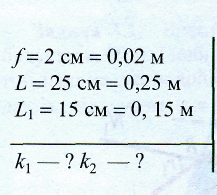3 рис. 3. видно, що коли предмет АВ знаходиться від ока на відстані найкращого бачення L, то кут зору

якщо ж цей предмет знаходиться поблизу фокуса лупи, і ми розглядаємо його крізь лупу, то його буде видно під кутом зору

За формулою лінійного збільшення лінзи

(а)

Підставивши у вираз (а) замість А'В' і АВ їхні значення через кути зору, одержимо

(б)

Оскільки уявне зображення знаходиться на відстані найкращого бачення, то b = L, й отже,

(в)

Врахувавши, що предмет знаходиться біля фокуса лупи, можна вважати a ~f. Звідси збільшення лупи приблизно можна визначити за формулою

(г)

Отже, збільшення для нормального ока, яке можна дістати за допомогою лупи,

для короткозорого ока —

Відповідь: ,

Задача 6.

З скла, що має показник заломлення n = 1,56, треба виготовити лінзу, оптична сила якої D = 8 діоптрій. Якими повинні бути радіуси кривизни лінзи, якщо вони однакові?

Розв’язання.

Дано: n = 1,56 м R -?

З формули лінзи маємо