3.Дослідження процесів в rlc-колах

Мета роботи: Експериментально дослідити резонансні явища в RLC колах.

Короткі теоретичні відомості.

У радіоелектроніці широко використовуються ланки, складені з котушок індуктивності і конденсаторів. Розглянемо процеси в найпростіших ланках – одна котушка індуктивності й один конденсатор. Такі схеми можуть бути частотними смуговими або режекторними фільтрами, тобто пропускають із всього діапазону частот лише певну смугу або, навпаки, не пропускають певну смугу частот.

Ураховуючи, що реальна котушка індуктивності має, крім індуктивності, ще й опір провідника, яким вона намотана, її еквівалентну схему можна зобразити у вигляді послідовного з’єднання ідеальної індуктивності (намотаної надпровідним дротом) і опору (так званий опір втрат котушки). Аналогічно можна розглядати і конденсатор, зважаючи на те, що діелектрик має певний опір. Опір діелектрика конденсатора дуже великий і ним у першому наближенні можна знехтувати. Крім того, в околі робочих частот коливального контуру паралельний опір конденсатора можна замінити еквівалентним послідовним. Отже, послідовно з’єднані котушку індуктивності і конденсатор можна аналізувати як схему, зображену на рис.1.

Рис. 1. Послідовний коливний контур.

Паралельне з’єднання котушки індуктивності і конденсатора можна зобразити однією з двох еквівалентних схем (рис. 2 ).

а б

Рис. 2. Паралельні коливні контури: а – з паралельним опором втрат; б – з послідовним опором втрат.

Ці схеми майже рівноправні в околі резонансної частоти (яку розглянемо нижче). Однак, слід пам’ятати, що на частотах, значно нижчих від резонансної, схема (див. рис. 2а) не відповідає паралельному з’єднанню котушки і конденсатора.

Розглянемо встановлений режим у колах (рис. 1 і рис. 2) у разі подання на них гармонічного сигналу. Цей режим широко використовується в радіоелектроніці.

Приєднаємо до схеми (рис. 1) джерело гармонічної напруги e = Eсos( t +  ). Застосовуючи комплексний метод аналізу, можна записати

.

Звідки

;

.

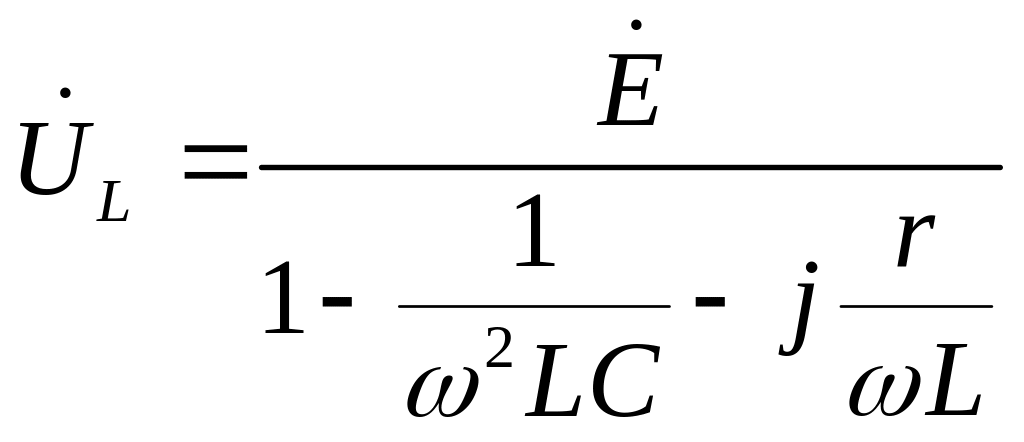Визначимо залежність амплітуди струму в колі від частоти:

.

З виразу видно, що при достатньо малому опорі r амплітуда струму різко зростає на частоті ω₀, тобто якщо .

Це явище відоме не тільки в радіотехніці, але і в інших розділах фізики під назвою резонанс, а частота називається резонансною. На рис. 5 показано залежність амплітуди струму від частоти для двох різних значень опору втрат контуру.

Як видно з рис. 5, з деяким наближенням можна вважати, що це коло проводить струм лише в деякій вузькій смузі частот в околі , тобто цю схему можна використати як смуговий фільтр (фільтр, який пропускає лише певну смугу частот). Ця смуга називається смугою пропускання. Для її кількісного визначення домовились вважати, що сигнал проходить, якщо його значення перевищує максимального значення (рис. 5).

З виразу видно, що значення частот на межі смуги пропускання визначаються з рівняння

.

Звідси отримуємо два додатні значення граничної частоти:

,

тобто ширина смуги пропускання

.

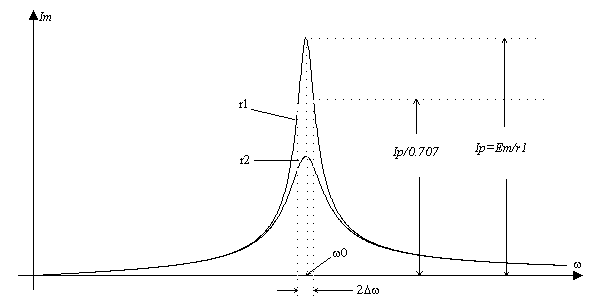
Рис. 5. Залежність амплітуди струму від частоти для двох різних значень опору втрат контуру

Відносна ширина смуги пропускання

,

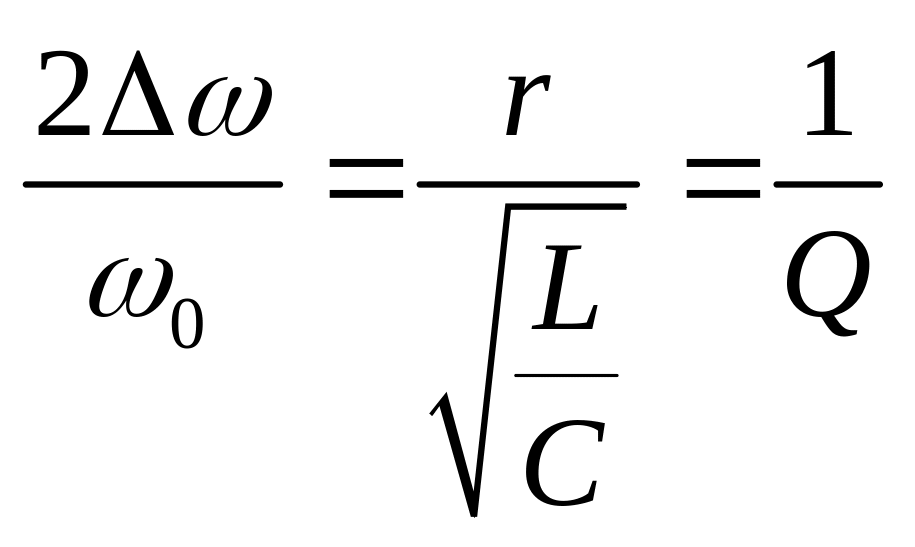де Q - добротність контуру. Величина називається характеристичним опором контуру і дорівнює модулю опору конденсатора ( ) або індуктивності ( ) на резонансній частоті. Отже, маємо декілька виразів для добротності контуру:

Як видно з для виділення вузької смуги частот необхідно мати високодобротний контур. На жаль, ця величина обмежена втратами в провіднику, яким намотана котушка, в феромагнітному осерді (яке вводять для збільшення індуктивності), в діелектрику конденсатора. Максимальна добротність, яку вдається отримати, становить десятки на низьких частотах (до сотні кілогерц) і 100200 на високих частотах.

Щоб визначити поведінку контуру в околі резонансної частоти, тобто якщо , вираз можна записати в більш зручному вигляді, використовуючи такі співвідношення:

,

де – відносне розстроєння частоти.

Ввівши загальне розстроєння частоти , можна записати

.

Врахувавши, що в околі резонансу частота суттєво не змінюється, вирази для напруг на ємності й індуктивності для високодобротного контуру можна записати так :

; .

З цих виразів видно, що при резонансі (= 0) напруга на ємності і індуктивності в Q разів перевищує прикладену до контуру напругу Е.

Для паралельного коливального контуру (рис. 2 а) можна записати .

Враховуючи, що ; ; , бачимо, що з математичного погляду ця схема еквівалентна схемі на рис. 1. Слід лише поміняти фізичні поняття змінних: струм – на напругу, напругу – на струм, опір – на провідність, ємність – на індуктивність і навпаки.

Звідси випливає, що можна зразу отримати аналогічні результати для схеми на рис. 2 а. Тобто залежність амплітуди встановленої напруги на контурі від частоти прикладеного джерела струму матиме вигляд, аналогічний як на рис. 5. Враховуючи вищезазначені заміни, вираз для добротності контуру можна записати так:

.

Знаменник виразу є комплексним опором послідовного контуру в околі резонансу. Залежність модуля цього опору (а отже і провідності паралельного контуру рис. 2 а) від частоти матиме вигляд, як на рис.6 а.

а

б

Рис. 6. Залежність модулів опору контурів від частоти: а – для послідовного контуру; б – для паралельного контуру.

Порівняємо провідності паралельних контурів на рис. 2 а і рис. 2 б. Для схеми на рис. 1 , для схеми на рис. 2 , або, враховуючи, що , отримаємо .

З цих виразів видно, що при дійсні та уявні частини провідностей і майже збігаються. Тобто схеми рис. 2 а і рис. 2 б майже еквівалентні в околі резонансної частоти при Якщо до послідовного контуру прикласти негармонічну періодичну напругу з таким періодом, щоб деяка гармоніка збігалася з резонансною частотою контуру, то можна простежувати явище множення частоти. Струми в колі для кожної гармоніки визначаються резонансною кривою (рис. 5). Якщо напруга гармоніки, частота якої збіглася з резонансною, не є набагато меншою від напруги максимальної гармоніки, то практично струм у колі буде гармонічним. Отже, і напруга на елементах контуру буде гармонічною і збігатиметься з частотою гармоніки.

Завдання.

1. Дослідити резонанс у послідовному коливальному контурі при різних добротностях. Для зміни добротності приєднати послідовно в контур з котушкою індуктивності та ємністю резистор. Зняти резонансні криві, визначити добротність контуру, його опір втрат, смугу пропускання контура.

2. Дослідити резонанс у паралельному контурі у випадку приєднання до нього джерела струму і джерела напруги для різних добротностей контуру.

Методичні вказівки.

1. Перехідні процеси в радіоелектронних схемах тривають долі секунд, мілісекунд або і мікросекунд. Спостерігати такий процес на звичайному осцилографі неможливо, бо промінь, швидко пробігши один раз по екрану осцилографа, не залишить помітного сліду. Для спостереження цього процесу необхідно періодично і синхронно повторювати його. Це можна зробити приєднавши до контура не постійну напругу, а періодичну послідовність прямокутних імпульсів. Адже прямокутні імпульси мають на певному проміжку часу постійну напругу, після чого напруга стає рівною нулю. Якщо вибрати тривалість імпульса і паузи більшою від тривалості перехідного процесу, то періодично буде повторюватися весь перехідний процес і його можна буде спостерігати на екрані осцилографа.

2. Струм в колі можна визначити з допомогою вольтметра, вимірявши ним напругу на відомому опорі і поділивши її на цей опір. При потребі в коло можна увімкнути достатньо малий додатковий відомий опір, який не впливав би на роботу схеми.

3. Для перетворення джерела напруги в джерело струму можна послідовно з джерелом приєднати достатньо великий опір (значно більший від опору навантаження).

Контрольні запитання.

1. Що таке добротність контура і чим вона визначається?

2. Чому дорівнює смуга пропускання послідовного контура? Виведіть формулу для смуги пропускання цього контура.

3. Нарисуйте графік залежності опору послідовного контура від частоти. Поясніть цю залежність.

4. Нарисуйте графік залежності опору паралельного контура від частоти. Поясніть цю залежність.

Лабораторна робота № 4