Тема 11. Вероятности оценки степени финансового риска

Цель: Изучить теоретический материал по данной теме, усвоить основные термины и понятия

Вопросы лекции

1. Финансовые риски.

2. Распределение вероятностей ставок доходности акций.

Содержание лекции

В предыдущих главах были подробно рассмотрены методы измерения и оценки степени риска. Здесь мы остановимся лишь на вероятностной оценке степени финансового риска.

Предположим, что купив акции А мы рассчитываем, что ди­видендный компонент будет равен 3%, ценовой компонент соста­вит 7%, так что ожидаемая ставка доходности будет равняться 10%: г = 3% + 7% = 10%.

Широко используемая единица измерения рискованности ак­тивов акции — это изменчивость (volatility). Изменчивость связана с диапазоном возможных ставок доходности акций и вероятностыо их получения. Чем шире диапазон между возможными показа­телями доходности и чем больше вероятность получения экстре­мальных значений, тем выше показатель изменчивости акции.

Например, если нас попросят дать «точечную оценку» доход­ности акций А в следующем году, то наш ответ будет 10%. При этом нас не удивит, если окажется, что реальная доходность ока­залась больше или меньше предсказанной нами. Доходность мо­жет быть как очень низкой (-50%), так и очень высокой (+50%). Чем сильнее расхождение межу возможными показателями доход­ности, тем сильнее изменчивость.

Чтобы лучше понять суть изменчивости, рассмотрим распре­деление вероятностей получения разных уровней доходности для акций А. Всем возможным уровням доходности соответствуют ве­роятности от нуля (полное отсутствие вероятности достижения этого уровня) до единицы (данная доходность будет получена обя­зательно).

Предположим, что нам абсолютно точно известно, что в бу­дущем году доходность составит 10%. В этом случае имеется толь­ко один возможный уровень доходности, и вероятность его дос­тижения равна 1,0.

Теперь допустим, что в зависимости от состояния экономики акции А могут принести разную доходность. Если в будущем году экономика будет на подъеме, объемы продаж и прибыль компа­нии будут повышаться, а значит, и ставка доходности инвести­ций в акции А будет равна 30%. Если в экономике будет спад, то ставка доходности составит — 10%, т.е. акционер понесет убыт­ки. Если экономическое положение просто останется неизменным, фактическая доходность составит 10%. Оценка вероятности для каждого из этих состояний в нашем гипотетическом примере по­казана в табл. 4.8 и проиллюстрирована рис. 4.12.

Таблица 4.8 Распределение вероятностей ставок доходности акций

Состояние экономики	Ставка доходности акций А	Вероятность
Подъем	30%	0,20
Нормальное	10%	0,60
Спад	-10%	0,20

Распределение вероятности в табл. 4.8 означает, что если мы вложим деньги в акции А, то получим, скорее всего, 10%-ную доходность. Вероятность этого в три раза превышает вероятность получения двух других значений доходности — 10% и 30%.

Распределение вероятностей доходности акций А к В

Состояние экономики	Ставка доходности акций В	Ставка доходности акций А	Вероятность
Подъем	50%	30%	0,20
Нормальное	10%	10%	0,60
Спад	-30%	-10%	0,20

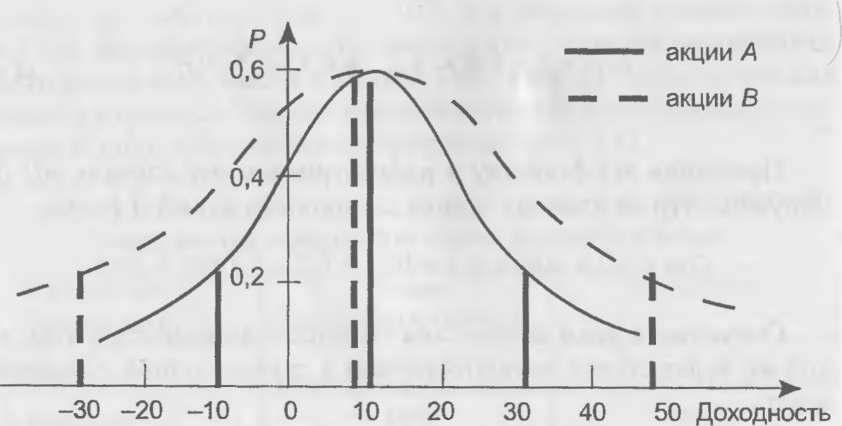
Рис. 4.13. Распределение вероятностей доходности акций А и В

(%)

Следует обратить внимание, что показатели вероятности оди­наковы для обеих акций, но у В более широкий диапазон колеба­ний доходности. Если экономика будет находиться на подъеме, акции В принесут своим акционерам 50% доходности, а акции А только 30%. Но, если экономическое положение ухудшится, до­ходность акций В упадет до -30%, а акций А — только до -10%. Другими словами, показатели доходности инвестиций в акции В изменяются более сильно, а, следовательно, они являются более рискованными.

Как было отмечено ранее, изменчивость показателей доходно­сти акций зависит от их возможного диапазона и от вероятности появления экстремальных значений. Для того, чтобы рассчитать и измерить изменчивость в распределении вероятностей получения возможных показателей доходности, в финансах чрезвычайно ши­роко используется среднее квадратическое отклонение <т (стандар­тное отклонение), которое для нашего примера мы определим как

п

<т²=£(г₍.-ВД)²-Р,., (4.64)

i=i

где математическое ожидание (среднее значение) равно:

п

= (4-65)

/=1

Чем больше стандартное отклонение, тем выше показатель изменчивости акций.

Для акций А и В имеем Еа (/",) = Ев(г,) = 10%.

Стандартное отклонение для акций А равно

ст] = (0,2)(30% -10%)² + (0,6)(10% -10%)² + (0,2)(—10% -10%)\

а_А =12,65%.

Стандартное отклонение для акций В равно

а²_в = (0,2)(50%-10%)² + (0,6)(10%-10%)² + (0,2)(-30% -10%)²,

а_н = 25,30%.

Стандартное отклонение для акций В в два раза больше, чем для А, поэтому возможное отклонение от среднего значения в два раза превышает тот же показатель у акций А.

В реальном мире диапазон показателей доходности акций не ограничен несколькими значениями, как в нашем примере, и до­ходность может принимать практически любое значение. Поэто­му мы можем сказать, что распределение доходностей акций пред­ставляет собой непрерывное распределение вероятностей. Чаще всего используется один из видов непрерывного распределения вероятностей — нормальное распределение, которое представля­ет собой кривую, показанную на рис. 4.13.

Более подробно о нормальном распределении мы поговорим в следующей главе.

Для нормального и прочих, похожих на него, симметричных распределений стандартное отклонение — естественная единица измерения изменчивости. Термины: изменчивость и стандартное отклонение часто используются как взаимозаменяемые.

Нормальное распределение охватывает неограниченное коли­чество значений доходности, от «минус бесконечность» до «плюс бесконечность». Для интерпретации различных значений стандар­тного отклонения обычно используется доверительный интервал

E(r_t)-to< X(rj)<E(r_t)+to, (4.66)

которым обозначается определенный диапазон значений (интер­вал), в пределах которого фактическая доходность акций попадет с заданной вероятностью.

Здесь А" (г,) — нормальная случайная величина с математичес­ким ожиданием E(r_t) и средним квадратическим отклонением а, a t — некоторый параметр. При t = 3 вероятность попадания слу­чайной величины X (r_t) в интервал (4.66) практически равна еди­нице.

Из формулы (4.66) следует, что при нормальном распределении доходность акции, которая находится в пределах доверительного интервала, включающего все значения доходности, находящиеся в рамках одного стандартного отклонения по обе стороны от сред­него значения, имеет вероятность порядка 0,68. Соответствующий доверительный интервал для двух стандартных отклонений имеет вероятность порядка 0,95, а доверительный интервал для трех стан­дартных отклонений имеет вероятность порядка 0,99.

Рассмотрим, например, акции с ожидаемой доходностью в 10% и стандартным отклонением в 20%. При нормальном распределе­нии существует вероятность, равная примерно 0,95, что фактичес­кая доходность попадет в интервал, ограниченный с одной сторо­ны ожидаемой доходностью и двумя стандартными отклонениями (10% + 2 • 20% = 50%), а с другой стороны — ожидаемой доходнос­тью минус два стандартных отклонения (10% - 2 - 20% = -30%). Диапазон доходности, который ограничен минимальным значе­нием -30% и максимальным значением 50%, с вероятностью 0,95 представляет собой доверительный интервал для доходности дан­ных акций.

Еще одним полезным показателем, применяемым при анализе финансовых рисков, является коэффициент вариации

Вопросы для самоконтроля

1. Финансовые риски.

2. Распределение вероятностей ставок доходности акций.

Рекомендуемая литература

1. Г.А. Абдрахманова Финансовые риски в экономической деятельности компании Алматы 2004г.

2. А.С. Шапкин Экономические и финансовые риски М 2006г.

3. В.А. Абчук Теория риска 2007г.

4. К. Рэдхэд, С. Хьюс. Управление финансовыми рисками. М., ИНФРА-М, 2006.*

5. Дж. К. Ван Хорн. Основы управления финансами. М., Финансы и статистика, 2007.*