
- •I Основные понятия и теоремы теории вероятностей
- •II Дискретные случайные величины
- •Дискретная случайная величина х задана законом распределения вероятностей
- •Дискретная случайная величина х задана законом распределения вероятностей
- •Дискретная случайная величина х задана законом распределения вероятностей
- •Дискретная случайная величина х задана законом распределения вероятностей
- •Дискретная случайная величина х задана законом распределения вероятностей
- •III Непрерывные случайные величины
- •IV Многомерные случайные величины
I Основные понятия и теоремы теории вероятностей
Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет нечетное число очков, равна ?
Операция сложения и умножения событий не обладают свойством: A(B+C) или A+B=B+A или AB=BA или A(BC)=A+B+C ?
Устройство состоит из двух элементов, работающих независимо. Вероятности безотказной работы этих элементов (в течение рабочего дня) соответственно равны 0,85 и 0,75. Тогда вероятность того, что в течение рабочего дня будет безотказно работать только один элемент, равна ?
В первой урне 8 черных и 2 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна ?
Из урны, в которой находятся одновременно 7 черных и 3 белых шаров, вынимают одновременно 2 шара. Тогда вероятность того, что оба шара будут черными, равна ?
Два студента сдают экзамен. Если ввести событие А (экзамен успешно сдал первый студент) и В (экзамен успешно сдал второй студент), то событие, заключающиеся в том, что экзамен успешно сдаст только один студент, будет предстпавлять собой выражение :
 или
или
 или АВ или
или АВ или
 ?
?
В урне лежат 12 шаров, среди которых 7 шаров белые. Наудачу по одному извлекают два шара без возвращения. Тогда вероятность того, что оба шара будут белыми, равна ?
С первого станка на сборку поступает 30%, со второго – 70% всех деталей. Среди деталей первого станка 80% стандартных, со второго – 90%. Наудачу взятая деталь оказалась стандартной. Тогда вероятность того, что она поступила на сборку с первого станка, равна?
За успешное участие в соревнованиях спотсмена могут наградить ценным призом (событие А), медалью (событие В), грамотой (событие С). Тогда событие, заключающееся в том, что случайно отобранный спортсмен награжден только грамотой, будет представлять собой выражение:
 или
или
 или
или
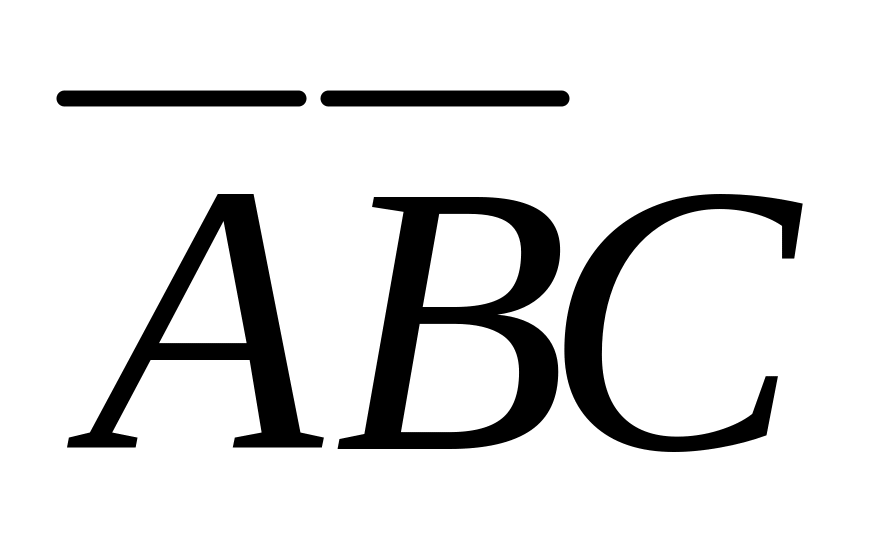 или
или
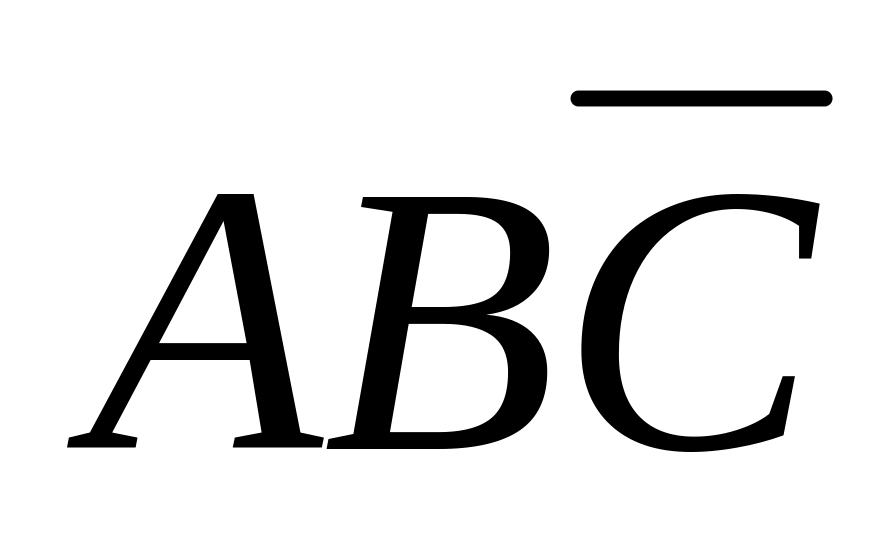 ?
?В ящике содержится 20 деталей, изготовленных на заводе №1, 30 деталей, изготовленных на заводе №2 и 50 деталей, изготовленных на заводе №3. Вероятность того, что деталь, изготовленная на заводе №1, отличного качества, равна 0,8; на заводе №2 – равна 0,7; на заводе №3 – равна 0,9. Тогда вероятность того, что наудачу извлеченная деталь окажется окличного качества, равна ?
II Дискретные случайные величины
Дискретная случайная величина Х задана законом распределения вероятностей
Х |
3 |
4 |
5 |
7 |
Р |
0,2 |
а |
0,3 |
0,1 |
Тогда значение а равно ?
Дискретная случайная величина х задана законом распределения вероятностей
Х |
2 |
4 |
6 |
Р |
0,1 |
0,2 |
0,7 |
Тогда ее функция распределения вероятностей имеет вид ?
Дискретная случайная величина х задана законом распределения вероятностей
Х |
-1 |
2 |
4 |
Р |
0,7 |
0,2 |
0,1 |
Тогда ее дисперсия равна ?
Проводится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна 0,8. Тогда математическое ожидание дискретной случайной величины Х – числа появления события А в n=100 проведенных испытаниях равна ?
Страховая компания заключила 1500 однотипных договоров страхования жизни сроком на один год с вероятностью наступления страхового случая, равной 0,001. Тогда вероятность того, что в течение года произойдет ровно три страховых случая, следует вычислить по формуле: Байеса или Пуассона или локальной формуле Лапласа или интегральной формуле Лапласа?
Матрица вероятностей перехода однородной цепи Маркова имеет вид
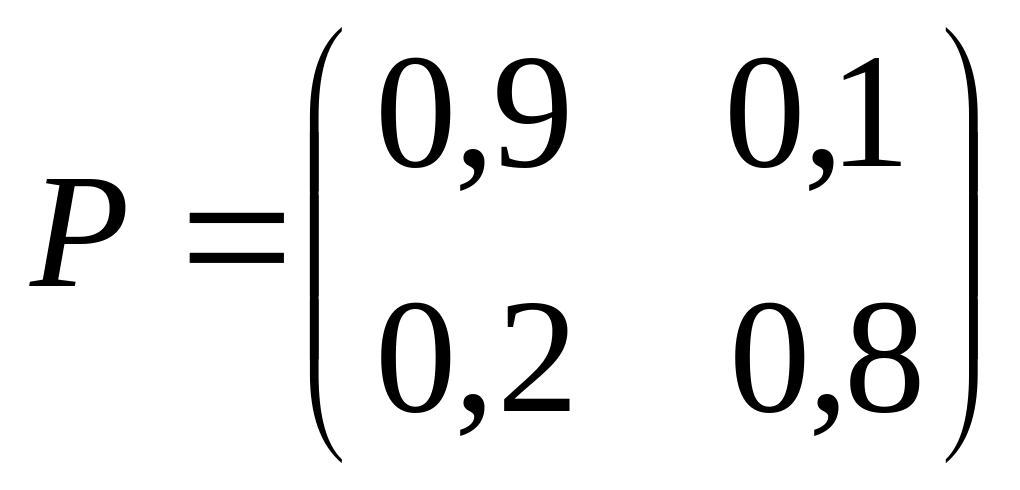 ,
а вектор вероятностей состояний цепи
Маркова на втором шаге равен
,
а вектор вероятностей состояний цепи
Маркова на втором шаге равен
 .
Тогда вектор состояний цепи Маркова
на четвертом шаге равен ?
.
Тогда вектор состояний цепи Маркова
на четвертом шаге равен ?
Вероятность поражения цели при одном выстреле равна 0,7. Тогда, вероятность того, что цель будет поражена хотя бы один раз, если произведено всего пять выстрелов, равна ?
Дискретная случайная величина Х задана законом распределения вероятностей
Х |
1 |
3 |
Р |
0,7 |
0,3 |
Тогда ее функция распределения вероятностей имеет вид ?
